Навигация
Если r ¹ 0, то заменим матрицу Е матрицей
3. Если r ¹ 0, то заменим матрицу Е матрицей
4. Заменим пару чисел (a,b) парой (b,r) и перейдём к шагу 1.
Если обозначить через Еk матрицу Е, возникающую в процессе работы алгоритма перед шагом 2 после k делений с остатком (шаг 1), то в обозначениях из доказательства теоремы 1 в этот момент выполняется векторное равенство (a,b)*Ek = (rk-1,rk). Его легко доказать индукцией по k. Поскольку числа a и b взаимно просты, имеем rn= 1, и это доказывает, что алгоритм действительно даёт решение уравнения ax + by = 1. Буквой n мы обозначили количество делений с остатком, которое в точности такое же, как и в алгоритме Евклида.
Полиномиальные алгоритмы в теории чисел – большая редкость. Да и оценки сложности алгоритмов чаще всего опираются на какие-либо не доказанные, но правдоподобные гипотезы, обычно относящиеся к аналитической теории чисел.
Для некоторых задач эффективные алгоритмы вообще не известны. Иногда в таких случаях всё же можно предложить последовательность действий, которая, «если повезёт», быстро приводит к требуемому результату. Существует класс так называемых вероятностных алгоритмов, которые дают правильный результат, но имеют вероятностную оценку времени работы. Обычно работа этих алгоритмов зависит от одного или нескольких параметров. В худшем случае они работают достаточно долго. Но удачный выбор параметра определяет быстрое завершение работы. Такие алгоритмы, если множество «хороших» значений параметров велико, на практике работают достаточно эффективно, хотя и не имеют хороших оценок сложности.
3. Полиномиальная арифметикаРассмотрим вероятностный алгоритм, позволяющий эффективно находить решения полиномиальных сравнений по простому модулю. Пусть p – простое число, которое предполагается большим, и f(x)ÎZ[x] – многочлен, степень которого предполагается ограниченной. Задача состоит в отыскании решений сравнения
f(x) º 0 (mod p). (1)
Например, речь может идти о решении квадратичных сравнений, если степень многочлена f(x) равна 2. Другими словами, мы должны отыскать в поле Fp = Z/pZ все элементы, удовлетворяющие уравнению f(x) = 0.
Согласно малой теореме Ферма, все элементы поля Fp являются однократными корнями многочлена xp - x. Поэтому, вычислив наибольший общий делитель d(x) = (xp - x, f(x)), мы найдём многочлен d(x), множество корней которого в поле Fp совпадает с множеством корней многочлена f(x), причём все эти корни однократны. Если окажется, что многочлен d(x) имеет нулевую степень, т. е. лежит в поле Fp, это будет означать, что сравнение (1) не имеет решений.
Для вычисления многочлена d(x) удобно сначала вычислить многочлен c(x)ºxp (mod f(x)), пользуясь алгоритмом, подобным описанному выше алгоритму возведения в степень (напомним, что число p предполагается большим). А затем с помощью аналога алгоритма Евклида вычислить d(x) = (c(x) – x, f(x)). Всё это выполняется за полиномиальное количество арифметических операций.
Таким образом, обсуждая далее задачу нахождения решений сравнения (1) мы можем предполагать, что в кольце многочленов Fp[x] справедливо равенство
f(x) = (x – a1)*…*(x – an), aiÎFp, ai ¹ aj.
3. 1 Алгоритм нахождения делителей многочлена f(x) в кольце Fp[x]
1. Выберем каким-либо способом элемент d Î Fp.
2. Вычислим наибольший общий делитель
g(x) = ( f(x), (x + d)(p-1)/2 – 1).
3. Если многочлен g(x) окажется собственным делителем f(x), то многочлен f(x) распадается на два множителя и с каждым из них независимо нужно будет проделать все операции, предписываемые настоящим алгоритмом для многочлена f(x).
4. Если окажется, что g(x) = 1 или g(x) = f(x), следует перейти к шагу 1 и, выбрав новое значение d, продолжить выполнение алгоритма.
Количество операций на шаге 2 оценивается величиной O(ln p), если вычисления проводить так, как это указывалось выше при нахождении d(x). Выясним теперь, сколь долго придётся выбирать числа d, пока на шаге 2 не будет найден собственный делитель f(x).
Количество решений уравнения (t + a1)(p – 1)/2 = (t + a2)(p – 1)/2 в поле Fpне превосходит (p-3)/2. Это означает, что подмножество D Ì Fp, состоящее из элементов d, удовлетворяющих условиям
(d + a1)(p – 1)/ 2 ¹ (d + a2)(p – 1)/ 2, d ¹ -a1, d ¹ -a2,
состоит не менее чем (p – 1)/2 из элементов. Учитывая теперь, что каждый ненулевой элемент bÎFp удовлетворяет одному из равенств b(p – 1)/2 = 1, либо b(p – 1)/2 = –1, заключаем, что для d Î D одно из чисел a1, a2 будет корнем многочлена (x + d) (p – 1)/2 – 1, а другое – нет. Для таких элементов d многочлен, определённый на шаге 2 алгоритма, будет собственным делителем многочлена f(x).
Итак, существует не менее (p –1)/2 «удачных» выборов элемента d, при которых на шаге 2 алгоритма многочлен f(x) распадается на два собственных множителя. Следовательно, при «случайном» выборе элемента d Î Fp, вероятность того, что многочлен не разложится на множители после k повторений шагов алгоритма 1-4, не превосходит 2-k. Вероятность с ростом k убывает очень быстро. И действительно, на практике этот алгоритм работает достаточно эффективно.
Заметим, что при оценке вероятности мы использовали только два корня многочлена f(x). При n > 2 эта вероятность, конечно, ещё меньше. Более тонкий анализ с использованием оценок А. Вейля для сумм характеров показывает, что вероятность для многочлена f(x) не распасться на множители при однократном проходе шагов алгоритма 1-4 не превосходит 2-n + O(p-1/2). Здесь постоянная в O(.) зависит от n. В настоящее время известно элементарное доказательство оценки А. Вейля.
Если в сравнении (1) заменить простой модуль p составным модулем m, то задача нахождения решений соответствующего сравнения становится намного более сложной. Известные алгоритмы её решения основаны на сведении сравнения к совокупности сравнений (1) по простым модулям – делителям m, и, следовательно, они требуют разложения числа m на простые сомножители, что, как уже указывалось, является достаточно трудоёмкой задачей.
Похожие работы
... системам линейных алгебраических уравнений с более чем одной неизвестной; MATLAB решает такие уравнения без вычисле-ния обратной матрицы. Хотя это и не является стандартным математическим обозначением, система MATLAB использует терминологию, связанную с обычным делением в одномерном случае, для описания общего случая решения совместной системы нескольких линейных уравнений. Два символа деления / ...
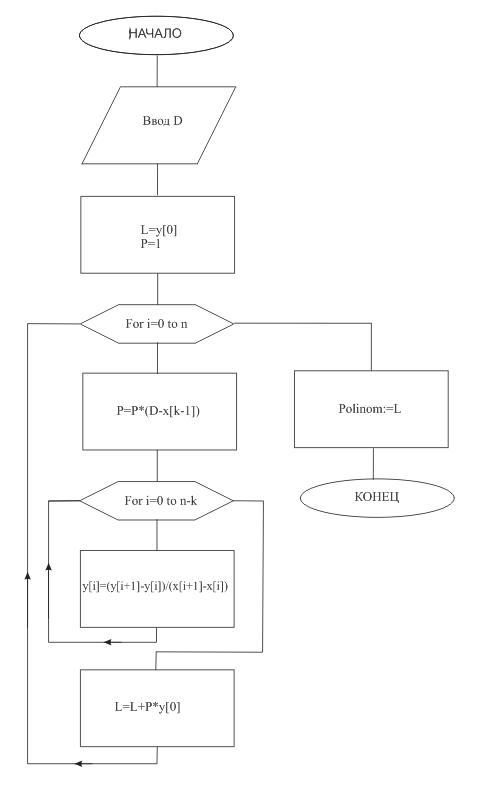
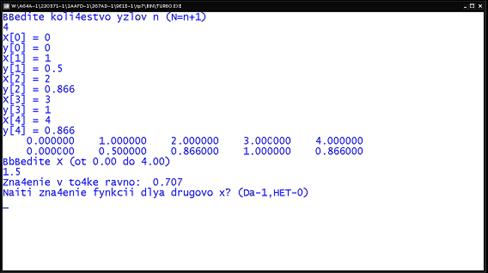
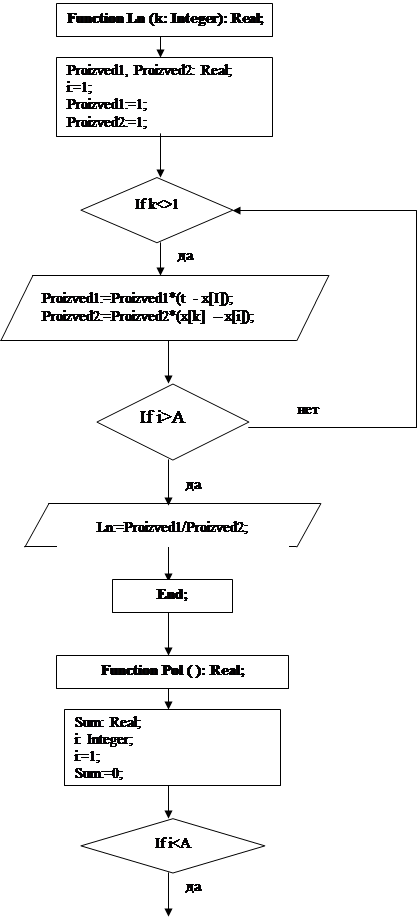
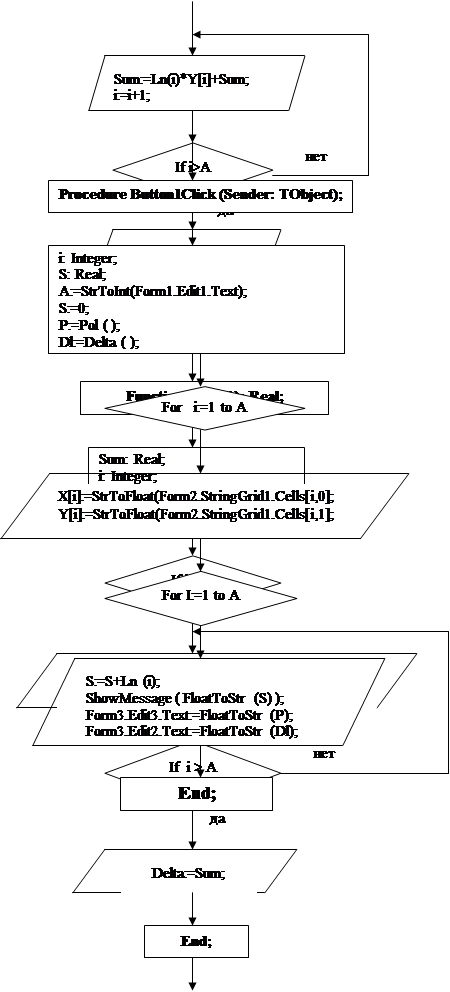
... Writeln(‘Федеральное агентство по образованию'); GoToXY(22,3); Writeln('Тульский государственный университет'); GoToXY(28,4); Writeln('КАФЕДРА РАДИОЭЛЕКТРОНИКИ'); GoToXY(14,8); Writeln('Интерполяция функции одной переменной методом Ньютона.'); GoToXY(27,9); Writeln('Построение графика полинома.'); GoToXY(34,12); Writeln('Вариант #7'); GoToXY(24,17); Writeln('Студент гр. 220371 ...
... должны быть прямоугольными. 5. Полиномы По степени применимости, по разнообразию и качеству соответствующих команд скалярные полиномы – следующие за матрицами математические объекты в MATLAB'е. Полином p(x)=anxn+an-1xn-1+...+a0 задается вектором-строкой p из чисел an, an-1, ... , a0, т.е. коэффициентами, расположенными в порядке убывания показателя степени. Его степень n задавать не ...
... порядке); конструктор (создает объект и инициализирует его состояние); деструктор (разрушает объект и освобождает занимаемую им память). В чистых объектно-ориентированных языках программирования операции могут объявляться только как методы – элементы классов, экземплярами которых являются объекты. Гибридные языки позволяют писать операции как свободные подпрограммы (вне классов). В общем ...




0 комментариев