Навигация
Произведение и возведение в степень многочленов, заданных массивами
34976
знаков
0
таблиц
3
изображения
3.2 Произведение и возведение в степень многочленов, заданных массивами
Условимся представлять многочлены массивами, индексированными, начиная с 0, в которых элемент с индексом i означает коэффициент многочлена степени i
type
Polynome=array[1..Nmax] of Ring_Element;
Следующий алгоритм даёт функцию умножения двух многочленов и , где многочлен степени (который даёт результат в конце алгоритма) должен быть предварительно инициализирован нулём.
for i:= 0 to degP do
for j:= 0 to degQ do
R[i+j]:=R[i+j]+P[i]*Q[i];
Изучая предыдущий алгоритм, устанавливаем, что его сложность как по числу перемножений, так и сложений, равна произведению высот двух многочленов: (deg P + 1)(degQ + 1), но в этом алгоритме, который не учитывает случай нулевых коэффициентов, можно рассматривать высоту многочлена как число всех коэффициентов. Значит, возможно улучшить предыдущий алгоритм, исключив все ненужные перемножения:
for i:= 0 to degP do
if P[i] ¹ 0 then
for j:= 0 to degQ do
if Q[j] ¹ 0 then
R[i+j]:=R[i+j]+P[i]Q[i];
Очень просто вычислить сложность алгоритма возведения в степень последовательными умножениями, если заметить, что когда P – многочлен степени d, то Pi – многочлен степени id. Если обозначить Cmul(n) сложность вычисления Pn, то рекуррентное соотношение Cmul(i + 1) = Cmul(i) + (d +1)(id +1) даёт нам:
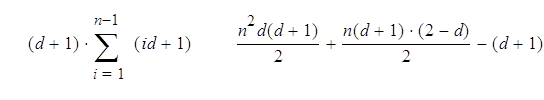
Cmul(n) = =
Что касается возведения в степень с помощью дихотомии (т.е. повторяющимися возведениями в квадрат), вычисления несколько сложнее: зная , вычисляем с мультипликативной сложностью. Как следствие имеем:
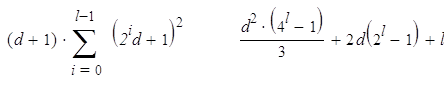
Csqr(2l) = = =
=
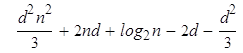
Предварительное заключение, которое можно вывести из предыдущих вычислений, складывается в пользу дихотомического возведения в степень: если n есть степень двойки (гипотеза ad hoc), этот алгоритм ещё выдерживает конкуренцию, даже если эта победа гораздо скромнее в данном контексте (n2d2/3 против n2d2/2), чем когда работаем в Z/pZ (2log2 n против n).
Но мы не учли корректирующие перемножения, которые должны быть выполнены, когда показатель не является степенью двойки. Если n = 2l+1 – 1, нужно добавить к последовательным возведениям в квадрат перемножения всех полученных многочленов. Умножение многочлена степени (2i-1)d на многочлен степени 2id вносит свой вклад из ((2i – 1)d + 1)( 2i d + 1) умножений, которые, будучи собранными по всем корректирующим вычислениям, дают дополнительную сложность:
= =
=
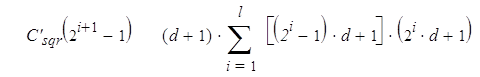
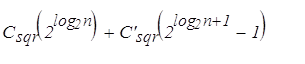
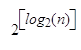Теперь можно заключить, что дихотомическое возведение в степень не всегда является лучшим способом для вычисления степени многочлена с помощью перемножений многочленов. Число перемножений базисного кольца, которые необходимы, Csqr(n), - в действительности заключено между ( ) и т.е. между n2d2/3 и 2n2d2/3, тогда как простой алгоритм требует всегда n2d2/2 перемножений. В частности, если исходный многочлен имеет степень, большую или равную 4, возведение в степень наивным методом требует меньше перемножений в базисном кольце, чем бинарное возведение в степень, когда n имеет форму 2l – 1.
Можно довольно просто доказать, что если n имеет вид 2l +2l – 1 + c (выражения, представляющие двоичное разложение n), то метод вычисления последовательными перемножениями лучше метода, использующего возведение в квадрат (этот последний метод требует корректирующего счёта ценой, по крайней мере, n2d2/9). Всё это доказывает, что наивный способ является лучшим для этого класса алгоритмов, по крайней мере, в половине случаев.
Действительно, МакКарти [3] доказал, что дихотомический алгоритм возведения в степень оптимален среди алгоритмов, оперирующих повторными умножениями, если действуют с плотными многочленами (антоним к разреженным) по модулю m, или с целыми и при условии оптимизации возведения в квадрат для сокращения его сложности наполовину (в этом случае сложность действительно падает приблизительно до n2d2/6 + n2d2/3 = n2d2/2).
Похожие работы
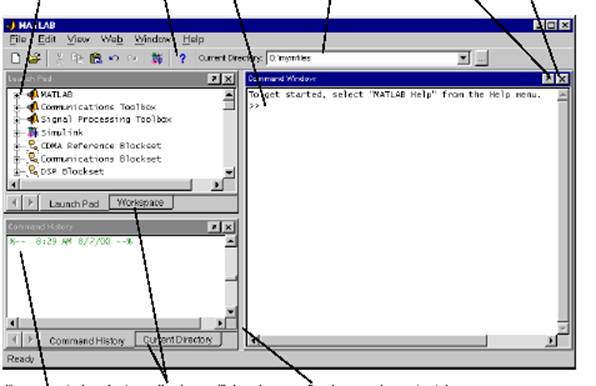
... системам линейных алгебраических уравнений с более чем одной неизвестной; MATLAB решает такие уравнения без вычисле-ния обратной матрицы. Хотя это и не является стандартным математическим обозначением, система MATLAB использует терминологию, связанную с обычным делением в одномерном случае, для описания общего случая решения совместной системы нескольких линейных уравнений. Два символа деления / ...
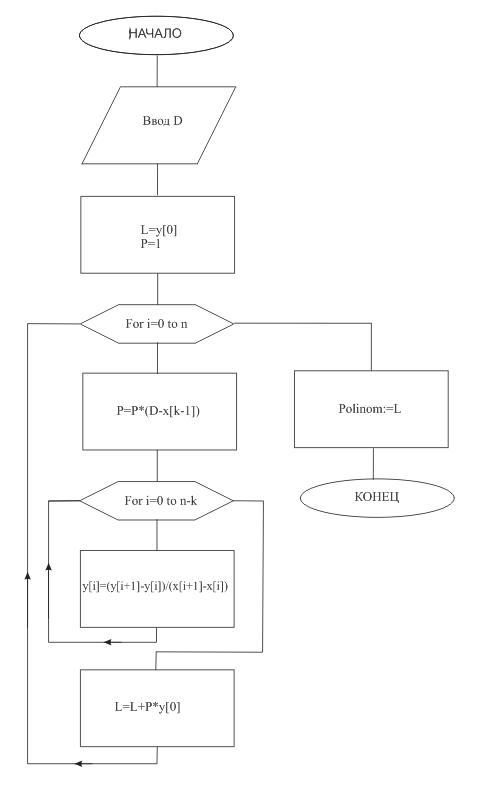
... Writeln(‘Федеральное агентство по образованию'); GoToXY(22,3); Writeln('Тульский государственный университет'); GoToXY(28,4); Writeln('КАФЕДРА РАДИОЭЛЕКТРОНИКИ'); GoToXY(14,8); Writeln('Интерполяция функции одной переменной методом Ньютона.'); GoToXY(27,9); Writeln('Построение графика полинома.'); GoToXY(34,12); Writeln('Вариант #7'); GoToXY(24,17); Writeln('Студент гр. 220371 ...
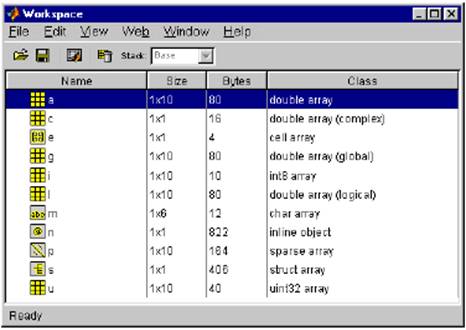
... должны быть прямоугольными. 5. Полиномы По степени применимости, по разнообразию и качеству соответствующих команд скалярные полиномы – следующие за матрицами математические объекты в MATLAB'е. Полином p(x)=anxn+an-1xn-1+...+a0 задается вектором-строкой p из чисел an, an-1, ... , a0, т.е. коэффициентами, расположенными в порядке убывания показателя степени. Его степень n задавать не ...
... порядке); конструктор (создает объект и инициализирует его состояние); деструктор (разрушает объект и освобождает занимаемую им память). В чистых объектно-ориентированных языках программирования операции могут объявляться только как методы – элементы классов, экземплярами которых являются объекты. Гибридные языки позволяют писать операции как свободные подпрограммы (вне классов). В общем ...
0 комментариев