Навигация
Государственный университет управления
Институт заочного обучения
Специальность – менеджмент
КОНТРОЛЬНАЯ РАБОТА
по дисциплине: Высшая математика.
Вариант № 1.
Выполнил студент Ганин Д.Ю.
Студенческий билет № 1211
Группа № УП4-1-98/2
Москва, 1999 г.
Содержание
Часть I.________________________________________________________ 3
Задание №2. Вопрос №9.________________________________________________________ 3
Задание №3. Вопрос №1.________________________________________________________ 3
Задание №12. Вопрос №9._______________________________________________________ 5
Задание №13. Вопрос №2._______________________________________________________ 5
Задание №18. Вопрос №9_______________________________________________________ 6
Часть II._______________________________________________________ 9
Задание №8. Вопрос №8.________________________________________________________ 9
Задание №12. Вопрос №9.______________________________________________________ 10
Задание №14. Вопрос №2.______________________________________________________ 10
Задание №15. Вопрос №6.______________________________________________________ 11
Задание №18. Вопрос №9.______________________________________________________ 12
Дополнительно Часть I._______________________________________ 13
Задание №7. Вопрос №1._______________________________________________________ 13
Задание №9. Вопрос №8._______________________________________________________ 13
Задание №11. Вопрос №6.______________________________________________________ 14
Задание №15. Вопрос №1.______________________________________________________ 15
Дополнительно Часть II._______________________________________ 15
Задание №7. Вопрос №1._______________________________________________________ 15
Задание №9. Вопрос №8._______________________________________________________ 16
Задание №11. Вопрос №6.______________________________________________________ 18
Задание №15. Вопрос №1.______________________________________________________ 18
Часть I. Задание №2. Вопрос №9.
В штате гаража числится 54 водителя. Сколько свободных дней может иметь каждый водитель в месяц (30 дней), если ежедневно 25% автомашин из имеющихся 60 остаются в гараже для профилактического ремонта.
Решение:|
| машин ежедневно остается в гараже на профилактическом ремонте. |
|
| машин с водителями ежедневно уходят в рейс. |
|
| водителей из штата гаража ежедневно не выходит в рейс из-за профилактического ремонта автомашин. |
|
| количество водителей в течение месяца, не выходящих в рейс из-за профилактического ремонта автомашин. |
|
| дней в месяц каждый водитель из штата гаража не выходит в рейс из-за профилактического ремонта автомашин. |
| Ответ: | Каждый водитель из штата гаража в течение месяца может иметь |
свободных дней.Построить график функции спроса Q=QD(P) и предложения Q=QS(P) и найдите координаты точки равновесия, если 
, 
.
Построим в плоскости POQ график функции спроса Q=QD(P) и предложения Q=QS(P). Для этого найдем координаты пересечения с осями координат:
| С осью OP (Q=0): | С осью OQ (P=0): | |
| Для Q=QS(P): | Для Q=QD(P): | |
|
|
|
|
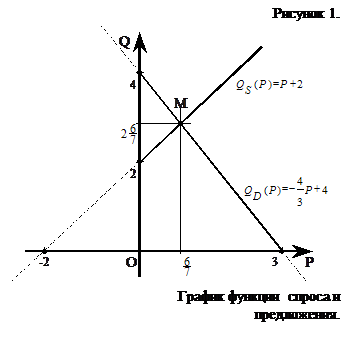Т.к. функции QS(P) и QD(P) – линейные функции, то их графиками являются прямые, для построения которых достаточно определить их точки пересечения с осями координат. Они найдены, значит можно производить построение графика (рис.1).
Найдем точку равновесия графиков функции спроса и предложения (М), в которой спрос равен предложению. Для этого решим систему:
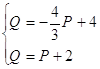, из этой системы получаем: 
, тогда 
, значит координаты т.M
.
| Ответ: | Координаты точки равновесия равны |
Задание №12. Вопрос №9.
Используя правила вычисления производных и таблицу, найдите производные следующих функций:
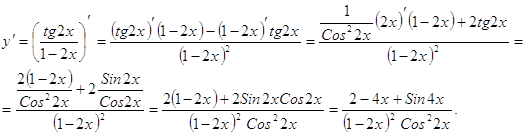
| Ответ: | Производная заданной функции равна |
Используя дифференциал функции, найдите приближенное значение
| числа: |
|
| Ответ: | Приближенное значение заданного числа равно 1,975. |
Задание №18. Вопрос №9
| Исследуйте функцию и постройте ее график: |
|
1. Область определения данной функции: 
.
2. Найдем точки пересечения с осями координат:
| С осью OY | С осью OX |
|
|
|
| Точка пересечения: | Точки пересечения: |
:
:
, дробь равна нулю, если ее числитель равен нулю, т.е.
, 
Похожие работы
Ось абсцисс пустим вдоль оси первого конуса, ось ординат - вдоль оси второго конуса, ось аппликат - параллельно оси цилиндра, причем так, чтобы система координат была правой. Расстояние d от вершин конусов до начала координат находим с помощью Теоремы Пифагора:2 + l = + 2 = 7.7 (см) таким образом ось цилиндра описывается следующим уравнением: Вершина первого конуса имеет следующие координаты - ...
урецкий, персидский, татарский и французский языки, а также мусульманское и международное право. Целью данной работы является освещение предмета высшей математики в профессиональной деятельности военного юриста. Работа включает не только теоретические аспекты применения методов высшей математики в военной юриспруденции, но и примеры практического использования методик. 1. Характеристика ...
... f ¢(xо) = 0, >0 (<0), то точка xоявляется точкой локального минимума (максимума) функции f(x). Если же =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные. На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b]. Пример 3.22. Найти экстремумы функции f(x) ...
бнику, решения задач необходимо ответить на вопросы для самопроверки, помещенные в конце темы. В соответствии с действующим учебным планом студенты-заочники изучают курс высшей математики в течение 1 и 2 семестра и выполняют в каждом семестре по две контрольные работы. Первая и вторая контрольные работы выполняются студентами в 1 семестре после изучения тем 1-2 и 3-4 соответственно. Третья и ...
0 комментариев