Навигация
Бэта-функции 6
Бэта – функции определяются интегралом Эйлера первого рода:
![]() =
=![]()
![]()
![]() (1.1)
(1.1)
сходятся при ![]() .Полагая
.Полагая ![]() =1 – t получим:
=1 – t получим:
![]() = -
= -![]() =
=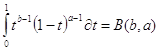
т.e. аргумент ![]() и
и ![]() входят в
входят в ![]() симетрично. Принимая во внимание тождество
симетрично. Принимая во внимание тождество
![]()
по формуле интегрирования почестям имеем
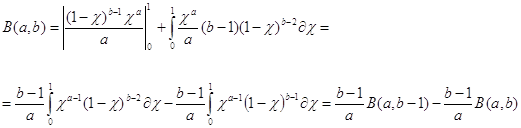
Откуда
![]() =
=![]() (1.2)
(1.2)
7
При целом b = n последовательно применяя(1.2)
Получим
 (1.3)
(1.3)
при целых ![]() = m,
= m,![]() = n,имеем
= n,имеем
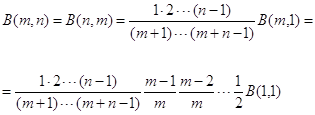
но B(1,1) = 1,следовательно:
![]()
![]()
![]()
Положим в (1.1) ![]() .Так как график функции
.Так как график функции ![]() симметрична относительно прямой
симметрична относительно прямой ![]() ,то
,то
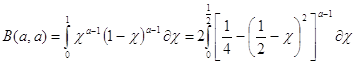
8
и в результате подстановки ![]() ,получаем
,получаем
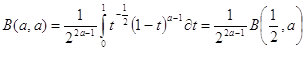
полагая в(1.1) ![]() ,откуда
,откуда ![]() ,получим
,получим
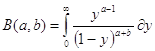 (1.4)
(1.4)
разделяя интеграл на два в пределах от 0 до 1 и от 1 до ![]() и применение ко второму интегралу подстановки
и применение ко второму интегралу подстановки ![]() ,получим
,получим
![]() =
=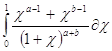
2. Гамма-функция 9
Гамма функцию определяет интеграл Эйлера второго рода
G(a) =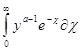
![]()
![]() (2.1)
(2.1)
сходящийся при ![]() 0.Положим
0.Положим ![]() =ty,t > 0 ,имеем
=ty,t > 0 ,имеем
G(a) =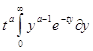
и после замены ![]() , через
, через ![]() и t через 1+t ,получим
и t через 1+t ,получим
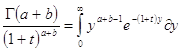
Умножая это равенство и интегрируя по t и пределах от 0 до![]() , имеем:
, имеем:
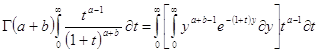
или на основании (1.4) и после изменения в правой части порядка интегрирования ,получаем:
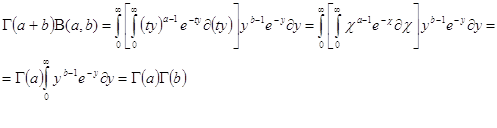
10
откуда
![]() (2.2)
(2.2)
заменяя в (2,1) ![]() ,на
,на ![]() и интегрируем по частям
и интегрируем по частям
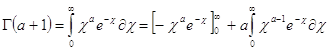
получаем рекурентною формулу
![]()
![]() (2.3)
(2.3)
![]()
так как
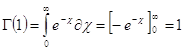
но при целом ![]() имеем
имеем
![]() (2.4)
(2.4)
то есть при целых значениях аргумента гамма-функция превращается в факториал.Порядок которого на единицу меньше взятого значения аргумента.При n=1 в (2.4) имеем
![]()
Интеграл
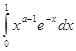
![]()
сходится при каждом ![]() ,поскольку
,поскольку ![]() ,и интеграл
,и интеграл ![]()
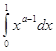 при
при ![]() сходится.
сходится.
В области ![]() , где
, где ![]() - произвольное положительное число, этот интеграл сходится равномерно, так как
- произвольное положительное число, этот интеграл сходится равномерно, так как![]() и можна применить признак Веерштраса. Сходящимся при всех значениях
и можна применить признак Веерштраса. Сходящимся при всех значениях ![]() является и весь интеграл
является и весь интеграл 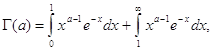 так как и второе слогаемое правой части является интегралом, заведомо сходящимся при любом
так как и второе слогаемое правой части является интегралом, заведомо сходящимся при любом![]() .Легко видеть что интеграл сходится по
.Легко видеть что интеграл сходится по![]() в любой области
в любой области ![]() где
где ![]() произвольно.Действительно для всех указаных значений
произвольно.Действительно для всех указаных значений ![]() и для всех
и для всех ![]()
![]() ,и так как
,и так как 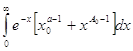 сходится, то выполнены условия признака Веерштрасса. Таким образом , в области
сходится, то выполнены условия признака Веерштрасса. Таким образом , в области ![]() интеграл
интеграл 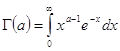 cходится равномерно.
cходится равномерно.![]()
Отсюда вытекает непрерывность гамма функции при![]() .Докажем дифференцируемость этой функции при
.Докажем дифференцируемость этой функции при ![]() .Заметим что функция
.Заметим что функция![]() непрерывна при
непрерывна при ![]() и
и![]() , и покажем ,что интеграл :
, и покажем ,что интеграл :
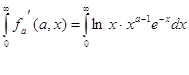
12
сходится равномерно на каждом сегменте ![]() ,
, ![]() . Выберем число
. Выберем число![]() так , чтобы
так , чтобы ![]() ; тогда
; тогда ![]() при
при ![]() .Поэтому существует число
.Поэтому существует число ![]() такое , что
такое , что ![]() и
и ![]() на
на![]() .Но тогда на
.Но тогда на ![]() справедливо неравенство
справедливо неравенство
![]()
и так как интеграл 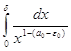 сходится, то интеграл
сходится, то интеграл 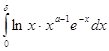 сходится равномерно относительно
сходится равномерно относительно ![]() на
на ![]() . Аналогично для
. Аналогично для ![]() существует такое число
существует такое число ![]() , что для всех
, что для всех ![]() выполняется неравенство
выполняется неравенство 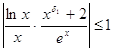 . При таких
. При таких ![]() и всех
и всех ![]() получим
получим ![]() , откуда в силу признака сравнения следует , что интеграл
, откуда в силу признака сравнения следует , что интеграл 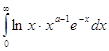 сходится равномерно относительно
сходится равномерно относительно ![]() на
на ![]() . Наконец , интеграл
. Наконец , интеграл
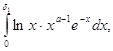
в котором подынтегральная функция непрерывна в области
![]() , очевидно, сходится равномерно относительно
, очевидно, сходится равномерно относительно ![]() на
на ![]() . Таким образом , на
. Таким образом , на ![]() интеграл
интеграл
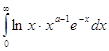
13
сходится равномерно , а, следовательно , гаммма функция бесконечно дифференцируема при любом ![]() и справедливо равенство
и справедливо равенство
![]()
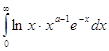 .
.
Относительно интеграла ![]() можна повторить теже рассуждения и заключить, что
можна повторить теже рассуждения и заключить, что
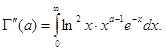
По индукции доказывается , что Г-функция бесконечно дифференцируема при![]() и для ее я
и для ее я ![]() -ой производной справедливо равенство
-ой производной справедливо равенство
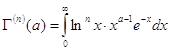
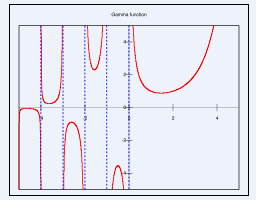
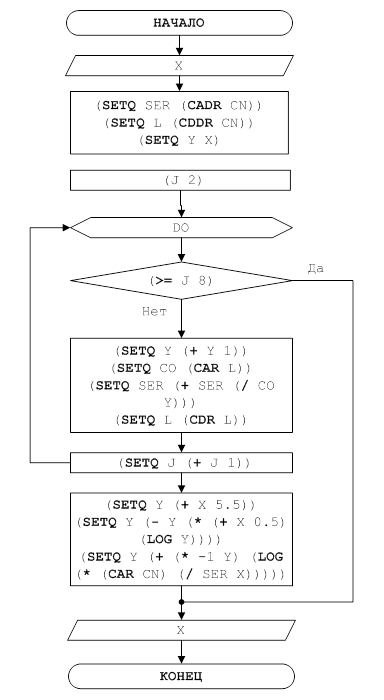
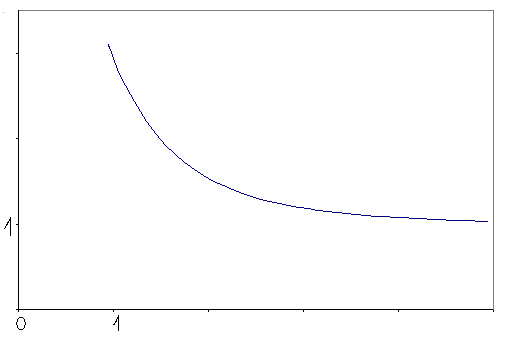
Изучим теперь поведение ![]() - функции и построим єскиз ее графика .
- функции и построим єскиз ее графика .
Из выражения для второй производной ![]() -функции видно, что
-функции видно, что ![]() для всех
для всех ![]() . Следовательно,
. Следовательно, ![]() возрастает. Поскольку
возрастает. Поскольку ![]() , то по теореме Роля на сегменте [1,2]производная
, то по теореме Роля на сегменте [1,2]производная ![]() при
при ![]() и
и![]() при
при ![]() , т. е. Монотонно убывает на
, т. е. Монотонно убывает на ![]() и монотонно возрастает на
и монотонно возрастает на ![]() . Далее , поскольку
. Далее , поскольку ![]() , то
, то ![]() при
при ![]() . При
. При ![]() из формулы
из формулы ![]() следует , что
следует , что ![]() при
при ![]() .
.
14
Равенство ![]() , справедливое при
, справедливое при ![]() , можно использовать при распространении
, можно использовать при распространении ![]() - функции на отрицательное значение
- функции на отрицательное значение ![]() .
.
Положим для![]() , что
, что ![]() . Правая часть этого равенства определена для
. Правая часть этого равенства определена для ![]() из (-1,0). Получаем, что так продолженная функция
из (-1,0). Получаем, что так продолженная функция ![]() принимает на (-1,0) отрицательные значения и при
принимает на (-1,0) отрицательные значения и при ![]() , а также при
, а также при ![]() функция
функция ![]() .
.
Определив таким образом ![]() на
на ![]() , мы можем по той же формуле продолжить ее на интервал (-2,-1). На этом интервале продолжением
, мы можем по той же формуле продолжить ее на интервал (-2,-1). На этом интервале продолжением ![]() окажется функция, принимающая положительные значения и такая, что
окажется функция, принимающая положительные значения и такая, что ![]()
![]()
![]() при
при ![]() и
и ![]() . Продолжая этот процесс, определим функцию
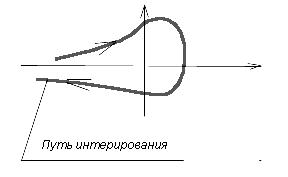
. Продолжая этот процесс, определим функцию ![]() , имеющею разрывы в целочисленных точках
, имеющею разрывы в целочисленных точках ![]() (см. рис.1)
(см. рис.1)
Отметим еще раз, что интеграл
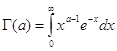
определяет Г-функцию только при положительных значениях ![]() , продолжение на отрицательные значения
, продолжение на отрицательные значения ![]() осуществлено нами формально с помощью формулы приведения
осуществлено нами формально с помощью формулы приведения ![]()
![]() .
.
15
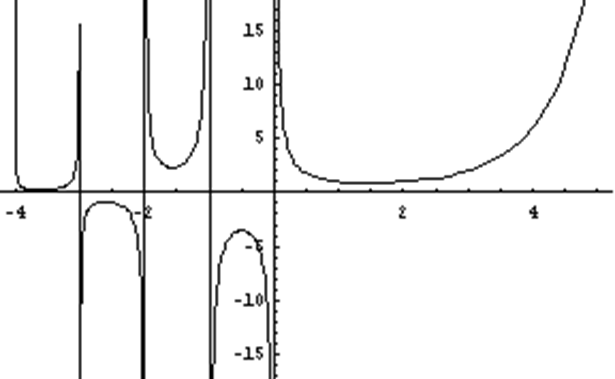
(рис.1)
Похожие работы
... функциях это уравнение не решается. Его решение называется гамма-функцией. Гамма-функцию можно записать в виде ряда или в виде интеграла. Для изучения глобальных свойств гамма-функции обычно пользуются интегральным представлением. 2.2 Интегральное представление Перейдем к решению этого уравнения. Будем искать решение в виде интеграла Лапласа: В этом случае правая часть уравнения ...
... к гамма-функции с положительным целым параметром, гамма-функции с положительным параметром, гамма-функции для множества точек. Созданная функциональная модель реализации основных способов вычисления гамма функции и ее программная реализация могут служить органической частью решения более сложных задач. СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ и литературы 1. Бронштейн, И.Н. Справочник по ...
... -функция непрерывна. Ввиду произвольности s0 ζ(s) непрерывна на всей области определения. Теперь почленным дифференцированием ряда (1), пока формально, найдём производную дзета-функции Римана: (2). Чтобы оправдать этот результат, достаточно удостовериться в том, что ряд (2) равномерно сходится на промежутке и воспользоваться теоремой о ...
... що найбільший теоретичний і прикладний інтерес представляє випадок викладений у другому розділі. Розділ 2 Всі результати першого розділу, що стосуються дзета-функції Римана, були отримані в припущенні, що її аргумент s – дійсне число. Однак, найвидатніші дослідження й численні важливі додатки стали можливі лише після включення в область визначення функції комплексних чисел. Уперше розглянув ...
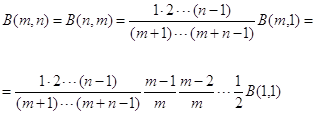
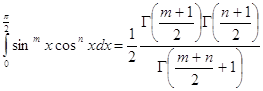


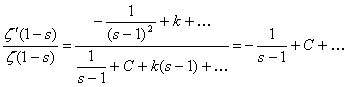
0 комментариев