Навигация
Вычисление некоторых интегралов. 16
4. Вычисление некоторых интегралов. 16
Формула Стирлинга
Применим гамма функцию к вычислению интеграла: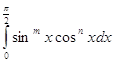
где m > -1,n > -1.Полагая , что ![]() ,имеем
,имеем
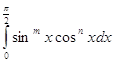
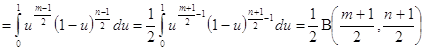
и на основании (2.2) имеем
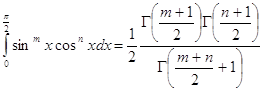 (3.1)
(3.1)
В интеграле
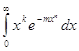
Где k > -1,n > 0,достаточно положить ![]()
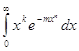
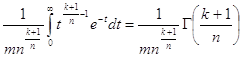
17
Интеграл
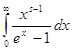
Где s > 0,разложить в ряд
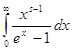


=![]()
где ![]() дзетта функция Римана
дзетта функция Римана
Рассмотрим неполные гамма функции (функции Прима)
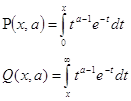
связанные неравенством
![]()
![]()
Разлагая,![]() в ряд имеем
в ряд имеем
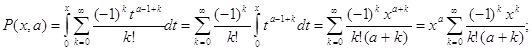
18
![]()
Переходя к выводу формулы Стирлинга , дающей в частности приближенное значение n! при больших значениях n ,рассмотрим предварительно вспомогательную функцию
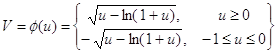 (3.2)
(3.2)
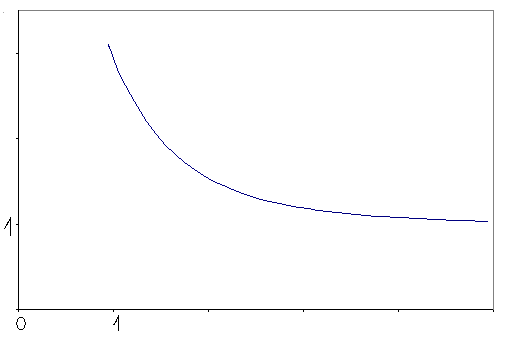
Непрерывна на интервале (-1,![]() ) монотонно возрастает от
) монотонно возрастает от ![]() до
до![]() при изменении
при изменении ![]() от
от ![]() до
до![]() и обращаются в 0 при u = 0.Так как
и обращаются в 0 при u = 0.Так как
![]()
то ![]() при u > 0 и при u < 0 , далее имеем
при u > 0 и при u < 0 , далее имеем
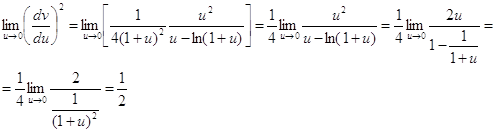
И так производная непрерывна и положительна во всем интервале ![]() ,удовлетворяет условию
,удовлетворяет условию
19
![]()
Из предыдущего следует, что существует обратная функция, ![]() определенная на интервале
определенная на интервале ![]() непрерывная и монотонно возрастающая в этом интервале,
непрерывная и монотонно возрастающая в этом интервале,
Обращающаяся в 0 при v=0 и удовлетворяющая условие
![]()
![]() (3.3)
(3.3)
Формулу Стирлинга выведем из равенства
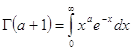
полагая ![]() ,имеем
,имеем
![]()
Положим далее ![]() введенная выше обратная функция, удовлетворяющая условиям u = -1при
введенная выше обратная функция, удовлетворяющая условиям u = -1при ![]() ,и
,и ![]() при
при ![]() .Замечая что(см.3.2)
.Замечая что(см.3.2)
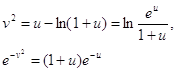
20
имеем
![]() ,
,
полагая на конец ,![]() ,получим
,получим
![]()
или
![]()
в пределе при ![]() т.е. при
т.е. при ![]() (см3.3)
(см3.3)
![]()
откуда вытекает формула Стирлинга
![]()
которую можно взять в виде
21
![]() (3.4)
(3.4)
где ![]() ,при
,при ![]()
![]()
для достаточно больших ![]() полагают
полагают
![]() (3.5)
(3.5)
вычисление же производится при помощи логарифмов
![]()
если ![]() целое положительное число, то
целое положительное число, то ![]() и (3.5) превращается в приближенную формулу вычисления факториалов при больших значениях n
и (3.5) превращается в приближенную формулу вычисления факториалов при больших значениях n
![]()
приведем без вывода более точную формулу
![]()
где в скобках стоит не сходящийся ряд.
5. Примеры вычисления интегралов 22
Для вычисления необходимы формулы:
![]()
![]()
Г(![]() )
)![]()
Вычислить интегралы
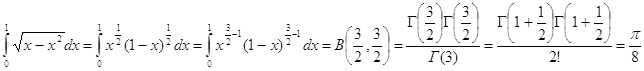
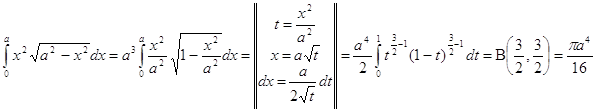
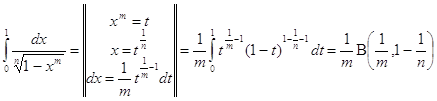
![]()

23
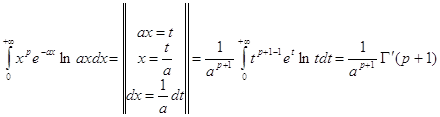
Запорізький державний університет
ДО ЗАХИСТУ ДОПУЩЕНИЙЗав. каф. Математичного аналізу
д. т. н. проф. ____ С.Ф. Шишканова
_________________________ 2002р.
ПОЯСНЮВАЛЬНА ЗАПИСКА ДО КУРСОВОГО ПРОЕКТУГАМА ФУНКЦІЇ
РозробивСт..гр.. 8221-2
Садигов Р.А.Керівник
Ст. викладач
Кудря В.І.Запоріжжя 2002.
Содержание Задание на курсовую работу........................... ...................................2Реферат............................................................. ...................................4
введение............................................................ ...................................5
1. Бета функции……………………………………………..............6
2. Гамма функции....................................... ...................................9
3. Производная гамма функции ............... ..................................11
4. Вычисление интегралов формула Стирлинга............................16
5. Примеры вычеслений............................. ..................................22
вывод................................................................ ..................................24
Список литературы……………………………………………..............25
Реферат
Курсовая работа: 24 ст., 5 источников, 1 рис.
Обьект иследований: гамма и ее приложения.
В работе идет речь о представлении бета и гамма функций с помощью интегралов Эйлера соответствено первого и второго рода. И о их применении для вычисления интегралов.
Ключевые слова:
ГАММА И БЕТА ФУНКЦИЯ, ИНТЕГРАЛ ЭЙЛЕРА, ПРОИЗВОДНАЯ, ПРЕДЕЛ.
Введение
Выделяют особый класс функций, представимых в виде собственого либо несобственого интеграла, который зависит не только от формальной переменной, а и от параметра.
Такие функции называются интегралами зависящими от параметра. К их числу относятся гамма и бета функции Эйлера.
Бета функции представимы интегралом Эйлера первого рода:

гамма функция представляется интегралом Эйлера второго рода:
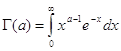
Вывод
Гамма функции являются удобным средством для вычисления некоторых интегралов в частности многих из тех интегралов, которые не представимы в элементарных функциях.
Благодаря этому они широко применяются в математике и ее приложениях, в механике, термодинамике и в других отраслях современной науки.
Список литературы 1. Специальные функции и их приложения: Лебедев И.И.,М.,Гостехтериоиздат,19532. Математический анализ часть 2:
Ильин О.А., Садовничий В.А., Сендов Бл.Х.,М.,”Московский университет”,1987
3. Сборник задач по математическому анализу:
Демидович Б.П.,М.,Наука,1966
4. Интегралы и ряды специальные функции:
Прудников А.П., Брычков Ю.А.,М.,Наука,1983
5. Специальные функции:
Кузнецов , М.,”Высшая школа”,1965
Похожие работы
... функциях это уравнение не решается. Его решение называется гамма-функцией. Гамма-функцию можно записать в виде ряда или в виде интеграла. Для изучения глобальных свойств гамма-функции обычно пользуются интегральным представлением. 2.2 Интегральное представление Перейдем к решению этого уравнения. Будем искать решение в виде интеграла Лапласа: В этом случае правая часть уравнения ...
... к гамма-функции с положительным целым параметром, гамма-функции с положительным параметром, гамма-функции для множества точек. Созданная функциональная модель реализации основных способов вычисления гамма функции и ее программная реализация могут служить органической частью решения более сложных задач. СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ и литературы 1. Бронштейн, И.Н. Справочник по ...
... -функция непрерывна. Ввиду произвольности s0 ζ(s) непрерывна на всей области определения. Теперь почленным дифференцированием ряда (1), пока формально, найдём производную дзета-функции Римана: (2). Чтобы оправдать этот результат, достаточно удостовериться в том, что ряд (2) равномерно сходится на промежутке и воспользоваться теоремой о ...
... що найбільший теоретичний і прикладний інтерес представляє випадок викладений у другому розділі. Розділ 2 Всі результати першого розділу, що стосуються дзета-функції Римана, були отримані в припущенні, що її аргумент s – дійсне число. Однак, найвидатніші дослідження й численні важливі додатки стали можливі лише після включення в область визначення функції комплексних чисел. Уперше розглянув ...
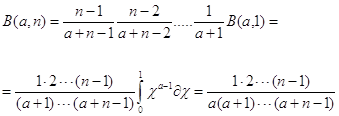
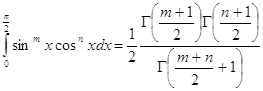
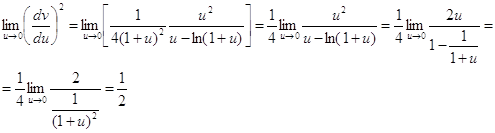
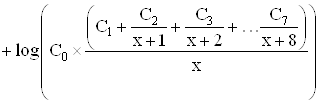

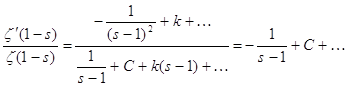
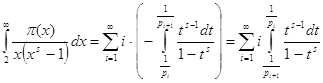

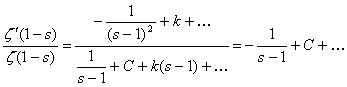
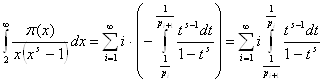
0 комментариев