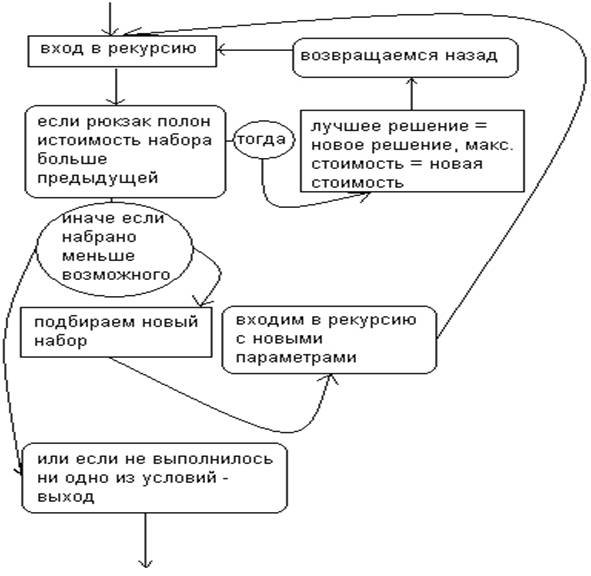
Навигация
2.3 Решение задачи о загрузке
Контрольная работа содержит вопросы по N различным темам. Каждый вопрос типа i имеет вес Vi(i=1,2,…N), а также время, отводимое на ответ Wi. Максимально время, которое может затратить студент на контрольную работу W. Требуется определить максимальное количество баллов (вес), которое может набрать студент за отведенное время W=30. Данные приведены в таблице:
| I | Wi | Vi |
| 1 2 3 4 5 6 7 8 | 2 3 1 4 7 5 3 2 | 2 3 2 4 6 5 4 2 |
Решить задачу, приведя ее к рекуррентным соотношениям.
Сначала рассмотрим задачу в общей постановке. Если обозначить количество вопросов типа і через ki, то задача принимает следующий вид:
![]()
при ограничениях
![]()
ki-неотрицательные числа.
Если отбросить требования целочисленности ki, то решение задачи нетрудно найти с помощью симплекс-метода (см. Приложение В). В самом деле, так как остается лишь одно ограничение, базисной будет только одна переменная, и задача сводится к выбору типа і, для которого величина viW/wi принимает максимальное значение. Исходная задача не является задачей линейного программирования, и для ее решения необходимо использовать метод динамического программирования. Следует отметить, что рассматриваемая задача может быть также решена с помощью методов целочисленного программирования.
Каждый из трех основных элементов модели ДП определяется следующим образом.
1. Этап j ставится в соответствии типу j, j=1,2,…,N.
2. Состояние yj на этапе j выражает суммарный вес вопросов, количество ответов на которые приняты на этапах j,j+1,…,N; при этом y1=W и yj=0,1,…,W при j=2,3,…,N.
3. Варианты решения kj на этапе j описываются количеством вопросов типа j. Значение kj заключено в пределах от нуля до [W/wj], где [W/wj]-целая часть числа (W/wj).
Пусть fi(yi)-максимальный суммарный вес вопросов, ответы на которые приняты на этапах j,j+1,…,N при заданном состоянии yj.
Рекуррентное соотношение (для процедуры обратной прогонки) имеет следующий вид:
![]()
![]()
Заметим, что максимальное допустимое значение kj ограничено величиной [yj/wj]. Это позволяет автоматически исключать все не являющиеся допустимыми варианты при заданном значении переменной состояния yj.
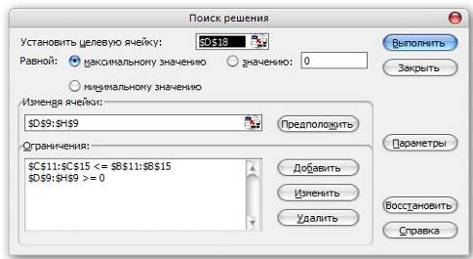
Решение исходной задачи (см. приложении А):
Этап 8.
![]()
Этап 7.
![]()
Этап 6.
![]()
Этап 5.
![]()
Этап 4.
![]()
Этап 3.
![]()
Этап 2.
![]()
Этап 1.
![]()
Оптимальное решение определяется теперь следующим образом. Из условия W=30 следует, что первый этап решения задачи при y1=30 дает оптимальное решение k1=0, которое означает, что на 0 (нуль) вопросов 1-го типа будут даны ответы. Далее находим:
| y1=30 | k1=0 |
| y2=y1-2*k1=30 | k2=0 |
| y3=y2-4*k2=30 | k3=4 |
| y4=y3-k3=26 | k4=1 |
| y5=y4-4*k4=22 | k5=0 |
| y6=y5-7*k5=22 | k6=0 |
| y7=y6-5*k6=22 | k7=5 |
| y8=y7-3*k7=7 | k8=7 |
Соответственно оптимальным решением задачи является (0,0,4,1,0,0,5,7), соответственно максимально количество баллов, которое студент может набрать за отведенное время равно 46.
Похожие работы
... задачи, то лучше потратить время на построение приближенного алгоритма, чем пытаться построить полиномиальный, или же, если это позволяют условия, использовать алгоритмы с экспоненциальной сложностью работы Глава 2 Методы решения задачи о рюкзаке 2.1 Классификация методов На практике очень часто возникают NP-полные задачи, задач о рюкзаке – одна из них . Конечно надежд, на то что для ...
... 0 505/103 0 792/103 669/103 500/103 Анализ Таблицы 6 позволяет сделать вывод о допустимости и оптимальности базиса XБ4=(x5, x7, x1, x2, x4)T. 3.4 Результат решения задачи планирования производства В результате решения поставленной задачи симплекс-методом получили набор производимой продукции x=(x1, x2, x3, x4, x5)=( 15145/103, 8910/103, 0, 1250/103, 3255/103), который удовлетворяет всем ...
... времени на возню с файлами на дисках или ожидание ввода, не смогут продемонстрировать какое-то впечатляющее увеличение скорости. 2. КЛАССИФИКАЦИЯ ЯЗЫКОВ ПРОГРАММИРОВАНИЯ 2.1. Машинно – ориентированные языки Машинно – ориентированные языки – это языки, наборы операторов и изобразительные средства которых существенно зависят от особенностей ЭВМ (внутреннего языка, структуры памяти и ...
... реакции или вмешательства оператора. Точки диалога по своей природе подразделяются на информационные (для ввода данных) и управляющие (для выбора дальнейшего хода обработки). Принятый в автоматизированной системе маркетинга одежды способ построения человеко-машинного диалога обеспечивает максимальную наглядность, простоту и удобство работы в режиме эксплуатации. 3. Определение емкости, оценка ...



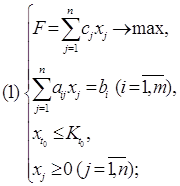
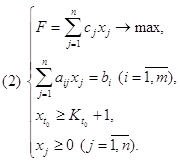
0 комментариев