Навигация
Анализ чувствительности решения
2.4 Анализ чувствительности решения
В таблице для первого этапа нам, по существу, необходимо получить оптимальное решение лишь для y1=30, так как это последний этап, подлежащий рассмотрению (см. Приложение А). Однако в таблицу включены вычисления для y1=0,1,…,30, которые позволяют провести анализ чувствительности решения.
Например, что произойдет, если время отводимое на контрольную работу будет 20, вместо 30 (см. Приложение А)?
| Y1=20 | k1=0 |
| Y2=y1-2*k1=20 | k2=0 |
| Y3=y2-4*k2=20 | k3=4 |
| Y4=y3-k3=16 | k4=0 |
| Y5=y4-4*k4=16 | k5=0 |
| Y6=y5-7*k5=16 | k6=0 |
| Y7=y6-5*k6=16 | k7=3 |
| Y8=y7-3*k7=7 | k8=7 |
соответственно максимально количество баллов, которое студент может набрать за отведенное время равно 34.
Что произойдет, если время отводимое на контрольную работу будет 5, вместо 30 (см. Приложение А)?
| y1=5 | k1=0 |
| y2=y1-2*k1=5 | k2=0 |
| y3=y2-4*k2=5 | k3=0 |
| y4=y3-k3=5 | k4=0 |
| y5=y4-4*k4=5 | k5=0 |
| y6=y5-7*k5=5 | k6=0 |
| y7=y6-5*k6=5 | k7=0 |
| Y8=y7-3*k7=5 | k8=5 |
соответственно максимально количество баллов, которое студент может набрать за отведенное время равно 10.
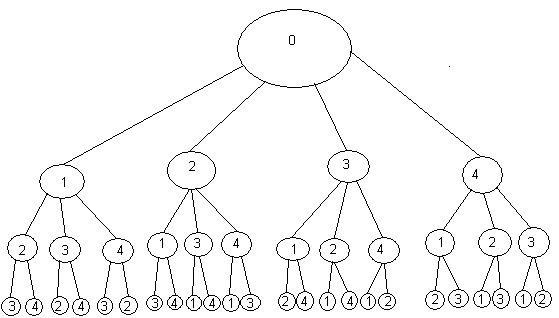
Что произойдет, если типов вопросов будет 4, вместо 8 (см. Приложение Б)?
Этап 4.
![]()
Этап 3.
![]()
Этап 2.
![]()
Этап 1.
![]()
| y1=30 | k1=5 |
| y2=y1-2*k1=20 | k2=3 |
| y3=y2-4*k2=8 | k3=4 |
| y4=y3-k3=4 | k4=3 |
соответственно максимально количество баллов, которое студент может набрать за отведенное время равно 39.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. Таха Х. Введение в исследование операций.–М.: Мир,1985.
2. Кузнецов Ю. Н. Математическое программирование. –М.: Наука,1976.
3. Вентцель Е. С. Исследование операций. –М.: Наука,1976.
4. Вентцель Е. С. Элементы динамического программирования. –М.: Наука,1987.
5. Акоф Р., Сасиени М. Основы исследования операций. –М.: Мир,1971.
6. Вентцель Е. С. Исследование операций: задачи, принципы, методология. –М.: Наука,1988.
7. Карманов В. Т. Математическое программирование. –М.:Наука,1986.
8. Зайченко Ю. П. Исследование операций. –К.: Высшая школа,1985.
9. Аоки М. Введение в методы оптимизации. –М.: Наука,1977.
10. Беллман Р., Дрейфус С. Прикладные задачи динамического программирования. –М.: Наука,1965.
11. Муну М. Математическое программирование. Теория алгоритмов. –М.: Наука,1990.
ПРИЛОЖЕНИЕ А Решение задачи методом динамического программирования
ПРИЛОЖЕНИЕ Б Анализ чувствительности решения
ПРИЛОЖЕНИЕ В Решение задачи симплекс-методом
Похожие работы
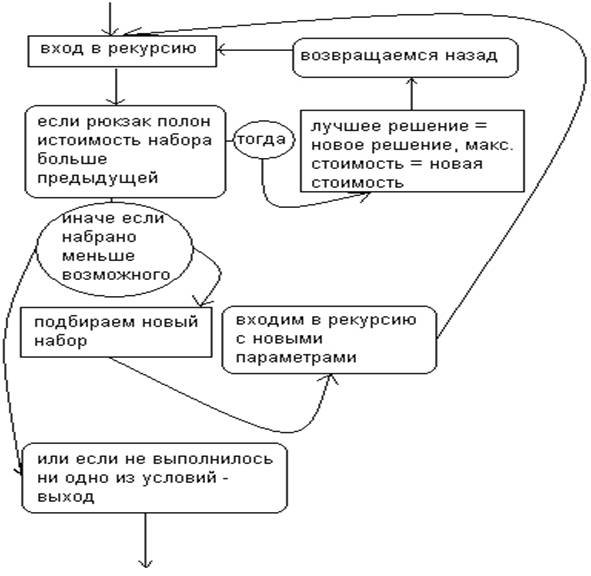
... задачи, то лучше потратить время на построение приближенного алгоритма, чем пытаться построить полиномиальный, или же, если это позволяют условия, использовать алгоритмы с экспоненциальной сложностью работы Глава 2 Методы решения задачи о рюкзаке 2.1 Классификация методов На практике очень часто возникают NP-полные задачи, задач о рюкзаке – одна из них . Конечно надежд, на то что для ...
... 0 505/103 0 792/103 669/103 500/103 Анализ Таблицы 6 позволяет сделать вывод о допустимости и оптимальности базиса XБ4=(x5, x7, x1, x2, x4)T. 3.4 Результат решения задачи планирования производства В результате решения поставленной задачи симплекс-методом получили набор производимой продукции x=(x1, x2, x3, x4, x5)=( 15145/103, 8910/103, 0, 1250/103, 3255/103), который удовлетворяет всем ...
... времени на возню с файлами на дисках или ожидание ввода, не смогут продемонстрировать какое-то впечатляющее увеличение скорости. 2. КЛАССИФИКАЦИЯ ЯЗЫКОВ ПРОГРАММИРОВАНИЯ 2.1. Машинно – ориентированные языки Машинно – ориентированные языки – это языки, наборы операторов и изобразительные средства которых существенно зависят от особенностей ЭВМ (внутреннего языка, структуры памяти и ...
... реакции или вмешательства оператора. Точки диалога по своей природе подразделяются на информационные (для ввода данных) и управляющие (для выбора дальнейшего хода обработки). Принятый в автоматизированной системе маркетинга одежды способ построения человеко-машинного диалога обеспечивает максимальную наглядность, простоту и удобство работы в режиме эксплуатации. 3. Определение емкости, оценка ...



0 комментариев