Навигация
1 FORMAT(I4/(5E15.7))
CALL KRIS(D,3,K,2,0,0.,0.)
END
4.9Результаты тестирования
Графики
вычисленных
путем решения
дифференциального
уравнения
функций приведены
на рисунке 4.
Видно, что они
близки к функциям
![]() и
и ![]() .
.
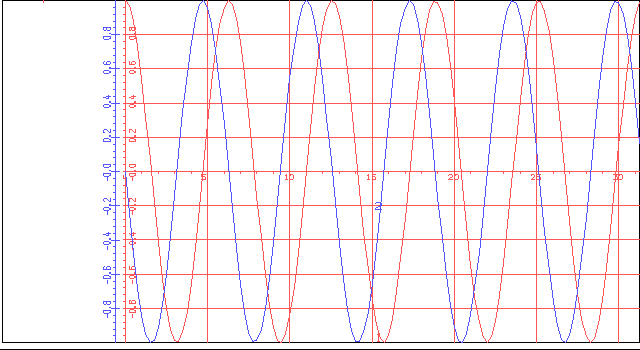
Рисунок 4
Амплитуды
колебаний равны
единице, период
![]() .
.
Выходной файл решения приведен ниже.
T=270 X(270)= 9.810482E-01
0
.1000000E+01 .9994009E+00 .9976879E+00 .9948635E+00 .9930583E+00
.9963406E+00 .9985125E+00 .9995713E+00 .9995162E+00 .9983473E+00
.9960660E+00 .9926749E+00 .9945613E+00 .9972748E+00 .9988768E+00
.9993657E+00 .9987408E+00 .9970031E+00 .9941545E+00 .9925186E+00
.9957730E+00 .9979174E+00 .9989495E+00 .9988685E+00 .9976745E+00
.9953687E+00 .9919540E+00 .9940073E+00 .9966935E+00 .9982686E+00
.9987311E+00 .9980807E+00 .9963180E+00 .9934454E+00 .9919787E+00
.9952052E+00 .9973223E+00 .9983279E+00 .9982209E+00 .9970015E+00
.9946712E+00 .9912329E+00 .9934532E+00 .9961117E+00 .1015252E+00
Значение функции в точке Т=270 отличается от точного примерно на 0,4% , а положительные максимумы отличаются от единицы не более , чем на 0,9% . При этом следует учесть, что в эту погрешность вошла и погрешность процедуры нахождения максимума с шагом, равным шагу интегрирования. Тенденции к затуханию или раскачиванию колебаний нет. Все это доказывает работоспособность алгоритма и программы.
4.10Квадратичная конечно-элементная модель усилителя 4.10.1 Описание алгоритма
Функция этого модуля заключается в том, что по заданной входной величине (обозначим ее Z3 ) выдается или величина U1, определяемая из таблицы 2, или величина U2, определяемая из таблицы 3. Эти таблицы представим в виде одного двухмерного массива W, в первой строке которого запишем табличные значения входной переменной Z3, а во второй и третьей строках - им соответствующие табличные значения переменных U1 и U2 . Значение еще одного входного параметра L ,- номера строки, будет определять, какую выходную переменную вычисляет модель (L=2 или L=3). Выходную переменную модуля обозначим U , а для модуля назначим имя US. Блок - схема алгоритма приведена на рисунке 5.
В цикле с индексом J определяется тот конечный элемент, в области которого находится входная величина Z3 , а затем вычисляется выходная величина по формуле Лагранжа с использованием L-той строки массива W.
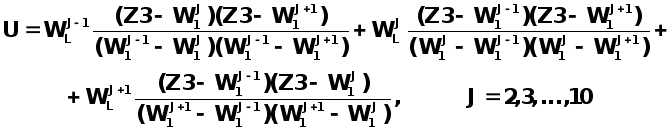
Если значение входной переменной Z3 выходит за пределы таблицы, определяющей характеристику усилителя, выводится сигнал об ошибке.
4.10.2Блок - схема алгоритма модели усилителя
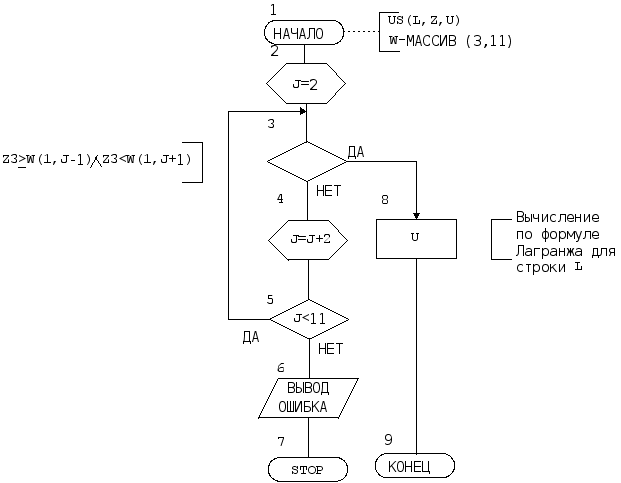
Рисунок 5
4.10.3Подпрограмма - модель усилителя
SUBROUTINE US(L,Z,U)
С Подпрограмма - модель усилителя.
DIMENSION W(3,11)
C характеристики усилителя из таблиц 2 и 3 по столбцам
DATA W /-3.125 ,-0.125 , 3. ,
= -2.85 , -0.1 , 2.75 ,
= -2.475 , -0.075 , 2.4 ,
= -1.78 , -0.05 , 1.73 ,
= -1.025 ,-0.025 , 1. ,
= -0.02 , 0. , 0.02
= 1.025 , 0.025 , -1. ,
= 1.78 , 0.05 , -1.73 ,
= 2.475 , 0.075 , -2.4 ,
= 2.85 , 0.1 , -2.75 ,
= 3.125 , 0.125 , -3. /
C Поиск интервала, заключающего Z3.
DO J=2, 10, 2
IF(Z3.GE.W(1,J-1).AND.Z3.LT. W(1,J+1)) GO TO 8
ENDDO
PRINT*, ‘ ОШИБКА ‘
STOP
C Формула Лагранжа.
8 U=W(L,J-1)*(Z3-W(1,J))*(Z3-W(1,J+1))/
= ((W(1,J-1)- W(1,J))*(W(1,J-1)-W(1,J+1)))+
= W(L,J)*(Z3-W(1,J-1))*(Z3-W(1,J+1))/
= ((W(1,J)-W(1,J-1))*(W(1,J)-W(1,J+1)))+
= W(L,J+1)*(Z3-W(1,J-1))*(Z3-W(1,J))/
= ((W(1,J+1)-W(1,J-1))*(W(1,J+1)-W(1,J)))
RETURN
END
4.10.4Решение тестовой задачи
В качестве тестовой задачи вычислим с малым шагом и построим графики характеристик усилителя.
DIMENSION D(3,1000)
READ*,XN,XK,DX
K=0
DO X=XN,XK,DX
K=K+1
С Вычисление значения входной переменной U1
CALL US(2,X,U1)
С Заполнение строки аргумента U1
D(1,K)=U1
С Вычисление значения выходной переменной усилителя U2.
CALL US(3,X,U2)
С Заполнение строки переменной U2.
D(2,K)=U2
ENDDO
CALL KRIS(D,3,K, 1, 1,0.,0.)
END

Рисунок 6
Из рисунка видно, что характеристика усилителя воспроизводится моделью правильно.
4.11Подпрограмма вычисления правых частей системы уравнений
В
подпрограмме
сохранены
наименования
переменных
модели.
Результаты
вычислений
заносятся, как
это требуют
подпрограммы
шага и управляющего
модуля, в первый
столбец массива
F,
который здесь,
для простоты
объявлен одномерным.
Для передачи
в этот модуль
изменяемого
от эксперимента
к эксперименту
параметра
генератора
![]() в общую область
включена переменная
TAU
.Остальные
переменные
общей области
нужны для связи
главного модуля
с подпрограммой
вывода результатов
шага.
в общую область
включена переменная
TAU
.Остальные
переменные
общей области
нужны для связи
главного модуля
с подпрограммой
вывода результатов
шага.
SUBROUTINE FUN(T,Z,F,N)
С Подпрограмма вычисления правых частей системы уравнений модели автогенератора.
DIMENSION Z(N*4),F(N*4),D(4,15000)
COMMON K,TZ,TAU,D
С Вызов подпрограммы - модели усилителя для вычисления входной величины U1
CALL US(2,Z(3),U1)
A=1/TAU
F(1)= - A*U1
F(2)=A*(Z(1)-5*U1)
F(3)=A*(Z(2)-6*U1)
RETURN
END
4.12Подпрограмма вывода
В подпрограмме сохранены наименования переменных модели.
Для того, чтобы иметь возможность хотя бы качественно, но быстро, оценивать правильность работы модели необходимо осуществить визуализацию решения. Поэтому в модуле вывода на каждом шаге вычислим входную и выходную переменные усилителя и заполним этими данными очередной столбец массива D. В этот же столбец запишем текущие значения времени Т . Массив D передадим через общую область в главный модуль, а оттуда подпрограмме построения графиков KRIS. В автогенераторе некоторое время длится процесс самовозбуждения. Нас интересует процесс установившихся колебаний, поэтому запись данных в массив будем делать только начиная с некоторого момента времени TZ. Эта величина и счетчик точек также включим в общую область.
SUBROUTINE PRIN(T,Z,F,N,IER)
С Подпрограмма вывода результатов шага.
DIMENSION Z(N*4),F(N*4),D(4,15000)
COMMON K,TZ,TAU,D
IF(T.GE.TZ)THEN
K=K+1
С Вычисление значения переменной входа U1.
CALL US(2,Z(3),U1)
C Вычисление значения переменной выхода U2.
CALL US(3,Z(3),U2)
С Заполнение массива.
D(1,K)=T
С Выход усилителя будет изображаться на графиках кривой номер 1.
D(2,K)=U2
С Вход усилителя будет изображаться на графиках кривой номер 2.
D(3,K)=U1
ENDIF
RETURN
END
4.13Главный модуль решения системы уравнений
В главном модуле в соответствие с требованиями подпрограммы метода Рунге - Кутта ARK объявим массивы для решения системы третьего порядка. Имена массивов сохраним такими же, как имена формальных параметров подпрограммы ARK. Зададим нулевые начальные условия и равные для всех интегральных переменных весовые коэффициенты погрешности. Из исходного файла будем вводить:
время начала записи данных в выходной массив TZ ,
параметр ![]() ,
,
время начала интегрирования ТN,
время конца интегрирования ТК,
максимальный шаг интегрирования НМ
задаваемую погрешность ЕР.
DIMENSION Z(12),RAB(9),F(12),D(4,15000)
С Главный модуль решения системы уравнений
EXTERNAL FUN,PRIN
COMMON K,TZ,TAU,D
С Задание начальных условий и весовых коэффициентов погрешности.
DO 1 K=1,3
Z(K)=0.
Похожие работы
... 7. В выводе сравните между собой вычисленное и измеренное значение силы тока и сделайте вывод о выполнении закона Ома. Отчет по лабораторной работе № 1 Исследование цепи переменного тока. выполненной учащим…… школы «Поиск» …………………………………………………………………………………… «…..»……….. 200….г Задание 1. Предварительные расчеты и измерения Емкость конденсатора: С =……… мкФ =………´ 10-6 Ф Индуктивность ...
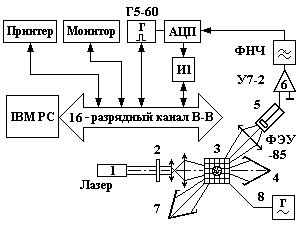
вает разностный сигнал постоянного тока. получаемый вычитанием сигналов постоянного тока 1-го и П-го каналов радиолокатора; Эти сигналы подается на стрелочные приборы; - вырабатывает разностные импульсные сигналы, получаемые вычитанием видеосигналов 1-го и П-го каналов радиолокатора; эти разностные сигналы подавтся на индикаторы ИКО/ИДВ и на индикатор типа "и". В плате ...
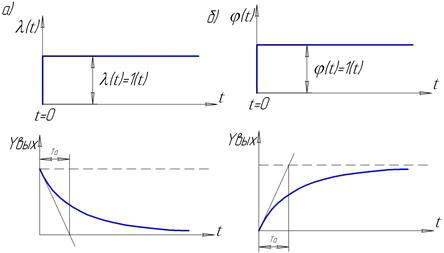
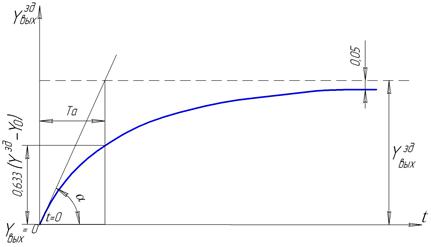
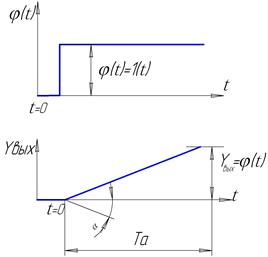
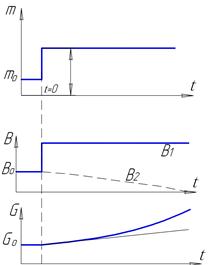
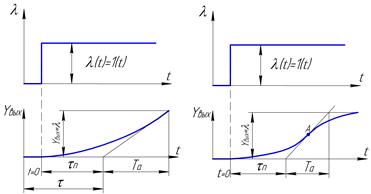
... – объекты, в которых регулируется расход жидкости или газа. Методы графического определения времени разгона Та для многоемкостных ОР приведены на рис. 5 и 6. Импульсные характеристики объектов регулирования Длительное и значительное по величине воздействие, которое приходится наносить для получения разгонных характеристик объекта регулирования, вызывает длительные изменение режима его работы ...
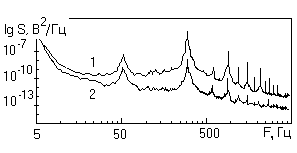
... наиболее полно использовать математические методы теории случайных процессов. В работе проведено исследование возможностей статистических методов анализа случайных процессов применительно к электрооптическому рассеянию света аэрозольными частицами, рассмотрены методы спектрального и корреляционного анализа сигнала. Твердые аэрозольные частицы неправильной формы, взвешенные в воздухе, находятся в ...
0 комментариев