Навигация
1 Z(K+3)=0.33333
READ*,TZ,TAU,TN,TK,HM,EP
K=0
С Решение системы.
CALL ARK(HM,TN,TK,Z,RAB,F,3,EP,FUN,PRIN,IER)
С Вывод результатов в форме графиков и таблиц.
CALL KRIS(D,4,K,2,1,0.,0.)
END
5.ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ АВТОГЕНЕРАТОРА 5.1Пробные решенияПробное решение выполним с параметрами, указанными в таблице 6
Таблица 6
| TZ |
| TN | TK | HM | EP |
| 0 | 1 | 0 | 370 | 1 | 0.0001 |
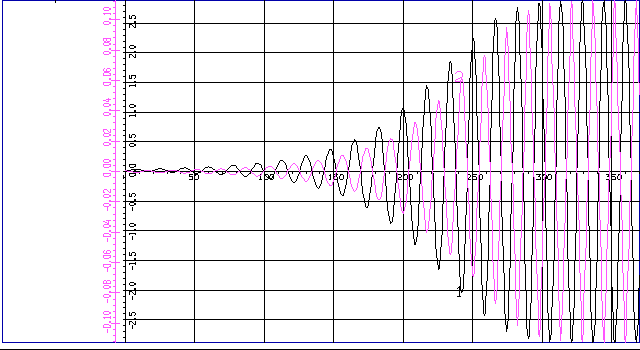
Рисунок 7
Из
рисунка видно,
что возбуждение
автогенератора
длится примерно
20 периодов
колебаний,
период колебания
примерно равен
16с., что составляет
![]() .
.
Второе решение выполним так, чтобы запись началась в режиме установившихся колебаний и длилась около двух периодов. Тогда по таблице решения можно с достаточной точностью установить амплитуду и период колебаний. Данные для второго решения приведены в таблице 7.
Таблица 7
| TZ |
| TN | TK | HM | EP |
| 370 | 1 | 0 | 400 | 1 | 0.0001 |
Графики решения приведены на Рисунке 8, а численные значения в таблице 8. Рисунок показывает, что выходное напряжение автогенератора (кривая 1) достаточно близко к синусоидальному, чего нельзя сказать о входном напряжении усилителя (кривая 2).
Таблица 8
АРГУМЕНТ ФУНКЦИЯ 1 ФУНКЦИЯ 2 ФУНКЦИЯ 3 ФУНКЦИЯ 4 ФУНКЦИЯ 5
370.0 -1.753 .5084E-01 .0000
370.5 -1.291 .3469E-01 .0000
371.0 -.7804 .1970E-01 .0000
371.5 -.2281 .6177E-02 .0000
372.0 .3466 -.8225E-02 .0000
372.5 .9243 -.2303E-01 .0000
373.0 1.476 -.4105E-01 .0000
373.5 1.974 -.5888E-01 .0000
374.0 2.395 -.7481E-01 .0000
374.0 2.395 -.7481E-01 .0000
374.5 2.699 -.9564E-01 .0000
375.0 2.860 -.1103 .0000
375.5 2.885 -.1127 .0000
376.0 2.792 -.1037 .0000
376.5 2.600 -.8794E-01 .0000
377.0 2.324 -.7205E-01 .0000
377.5 1.961 -.5838E-01 .0000
378.0 1.527 -.4280E-01 .0000
378.5 1.038 -.2625E-01 .0000
379.0 .5052 -.1226E-01 .0000
379.5 -.5797E-01 .1948E-02 .0000
380.0 -.6338 .1614E-01 .0000
380.5 -1.202 .3169E-01 .0000
381.0 -1.729 .4996E-01 .0000
381.5 -2.190 .6695E-01 .0000
382.0 -2.559 .8495E-01 .0000
382.5 -2.793 .1038 .0000
383.0 -2.885 .1127 .0000
383.5 -2.849 .1092 .0000
384.0 -2.706 .9619E-01 .0000
384.5 -2.472 .7926E-01 .0000
385.0 -2.152 .6553E-01 .0000
385.5 -1.753 .5082E-01 .0000
386.0 -1.290 .3467E-01 .0000
386.5 -.7795 .1968E-01 .0000
387.0 -.2272 .6154E-02 .0000
387.5 .3476 -.8250E-02 .0000
388.0 .9253 -.2306E-01 .0000
388.5 1.477 -.4108E-01 .0000
389.0 1.975 -.5892E-01 .0000
389.5 2.396 -.7484E-01 .0000
389.5 2.396 -.7484E-01 .0000
390.0 2.699 -.9568E-01 .0000
390.5 2.861 -.1103 .0000
391.0 2.885 -.1127 .0000
391.5 2.791 -.1037 .0000
392.0 2.600 -.8792E-01 .0000
392.5 2.323 -.7203E-01 .0000
393.0 1.960 -.5836E-01 .0000
393.5 1.526 -.4277E-01 .0000
394.0 1.037 -.2622E-01 .0000
394.5 .5042 -.1223E-01 .0000
395.0 -.5907E-01 .1975E-02 .0000
395.5 -.6350 .1617E-01 .0000
396.0 -1.203 .3172E-01 .0000
396.5 -1.730 .4999E-01 .0000
397.0 -2.191 .6699E-01 .0000
397.5 -2.560 .8500E-01 .0000
398.0 -2.793 .1039 .0000
398.5 -2.885 .1127 .0000
399.0 -2.849 .1091 .0000
399.5 -2.705 .9616E-01 .0000
400.0 -2.472 .7922E-01 .0000
Из этой таблицы находим период и амплитуду колебаний выходного напряжения, а также коэффициент усиления, как отношение выходного напряжения ко входному. Результаты заносим в таблицу 10

Рисунок 8
5.2Решение для спектрального анализа выходного напряжения
Выделим один период колебаний и сделаем третье решение.
Таблица 9
| TZ |
| TN | TK | HM | EP |
| 379,5 | 1 | 0 | 395 | 1 | 0.0001 |
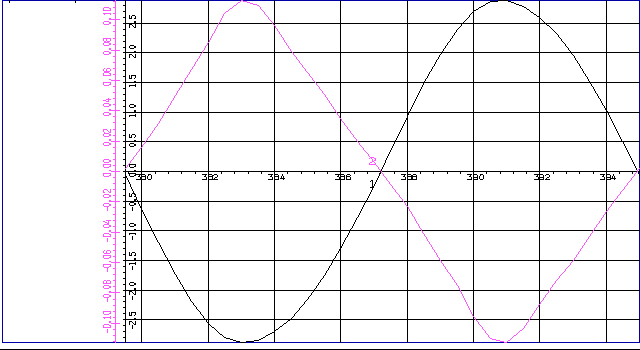
Рисунок 9
Таблица 9
АРГУМЕНТ ФУНКЦИЯ 1 ФУНКЦИЯ 2 ФУНКЦИЯ 3 ФУНКЦИЯ 4 ФУНКЦИЯ 5
379.5 -.5797E-01 .1948E-02 .0000
380.0 -.6338 .1614E-01 .0000
380.5 -1.202 .3169E-01 .0000
381.0 -1.729 .4996E-01 .0000
381.5 -2.190 .6695E-01 .0000
382.0 -2.559 .8495E-01 .0000
382.5 -2.793 .1038 .0000
383.0 -2.885 .1127 .0000
383.5 -2.849 .1092 .0000
384.0 -2.706 .9619E-01 .0000
384.5 -2.472 .7926E-01 .0000
385.0 -2.152 .6553E-01 .0000
385.5 -1.753 .5082E-01 .0000
386.0 -1.290 .3467E-01 .0000
386.5 -.7795 .1968E-01 .0000
387.0 -.2272 .6154E-02 .0000
387.5 .3476 -.8250E-02 .0000
388.0 .9253 -.2306E-01 .0000
388.5 1.477 -.4108E-01 .0000
389.0 1.975 -.5892E-01 .0000
389.5 2.396 -.7484E-01 .0000
389.5 2.396 -.7484E-01 .0000
390.0 2.699 -.9568E-01 .0000
390.5 2.861 -.1103 .0000
391.0 2.885 -.1127 .0000
391.5 2.791 -.1037 .0000
392.0 2.600 -.8792E-01 .0000
392.5 2.323 -.7203E-01 .0000
393.0 1.960 -.5836E-01 .0000
393.5 1.526 -.4277E-01 .0000
394.0 1.037 -.2622E-01 .0000
394.5 .5042 -.1223E-01 .0000
395.0 -.5907E-01 .1975E-02 .0000
5.3Решения для установления зависимостей параметров от
Изменяя величину ![]() ,
делаем решения,
аналогичные
второму, и
результаты,
извлеченные
из выходных
файлов, заносим
в таблицу 10.
,
делаем решения,
аналогичные
второму, и
результаты,
извлеченные
из выходных
файлов, заносим
в таблицу 10.
Таблица 10
| TZ |
| TN | TK | HM | EP | Т | U1MAX | U2MAX | КУС |
| 370 | 1 | 0 | 400 | 1 | 0,0001 | 15,5 | 0,1127 | 2,885 | 25,6 |
| 3200 | 10 | 0 | 3700 | 10 | 0,0001 | 155 | 0,1127 | 2,884 | 25,59 |
| 16000 | 50 | 0 | 20000 | 40 | 0,0001 | 780 | 0,1128 | 2,886 | 25,85 |
| 32000 | 100 | 0 | 36000 | 80 | 0,0001 | 1560 | 0,1129 | 2,886 | 25,62 |
Анализируя
эти результаты,
приходим к
выводу, что
период колебаний
пропорционален
![]() .
.
![]() (
17 )
(
17 )
Амплитуды колебаний и коэффициент усиления практически постоянны. Их незначительные изменения вызваны, скорее всего погрешностями наших численных экспериментов.
6.ПРОГРАММЫ ОБРАБОТКИ РЕЗУЛЬТАТОВ МОДЕЛИРОВАНИЯ 6.1Программа численного интегрирования по методу трапеций
Для
вычисления
амплитуды An n-ой
гармоники 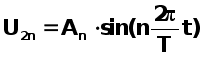 выходного
напряжения от
ее номера n
необходимо
несколько раз
вычислять
определенный
интеграл
выходного
напряжения от
ее номера n
необходимо
несколько раз
вычислять
определенный
интеграл 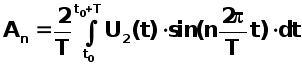 ,
,
Функция
![]() на периоде
на периоде
![]() вычислена нами
и представлена
в таблице 9.
Подынтегральную
функцию получим,
умножая в каждой
точке таблицы
вычислена нами
и представлена
в таблице 9.
Подынтегральную
функцию получим,
умножая в каждой
точке таблицы
![]() величину
величину ![]() на значение
на значение 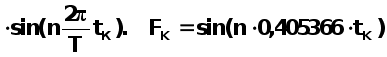 . Применяя формулу
трапеций, интеграл
заменим суммой
. Применяя формулу
трапеций, интеграл
заменим суммой
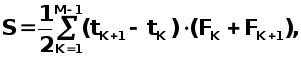 (
18 )
(
18 )
где М=33 ,- количество точек в таблице 9.
Тогда амплитуду n-ой гармоники можно вычислить, как
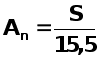 (
19 )
(
19 )
Вычислим в цикле амплитуды девяти гармоник и занесем их в массив D для построения графика с помощью подпрограммы KRIS.
Блок - схема и программа вычисления амплитуд гармоник приведены ниже.
DIMENSION T(200),U2(200),F(200),A(9),D(2,9)
READ*,M,L,(T(K),U2(K),X,Y,K=1,M)
DO N=1,9
DO K=1,M,L
F(K)=U2(K)*SIN(N*0.405366*T(K))
ENDDO
S=0
DO K=1,M-1,L
S=S+(T(K+1)-T(K))*(F(K)+F(K+1))
ENDDO
A(N)=S/15.5
D(1,N)=N
D(2,N)=A(N)
ENDDO
CALL KRIS(D,2,9,1,0,0.,0.)
PRINT16,(N,A(N),N=1,9)
16 FORMAT(I4,E14.6)
END
Изменение шага L позволяет оценить погрешность интегрирования. Переменные X и Y нужны в списке ввода для считывания данных прямо из выходного файла третьего решения.
6.2Блок - схема алгоритма вычисления амплитуд гармоник
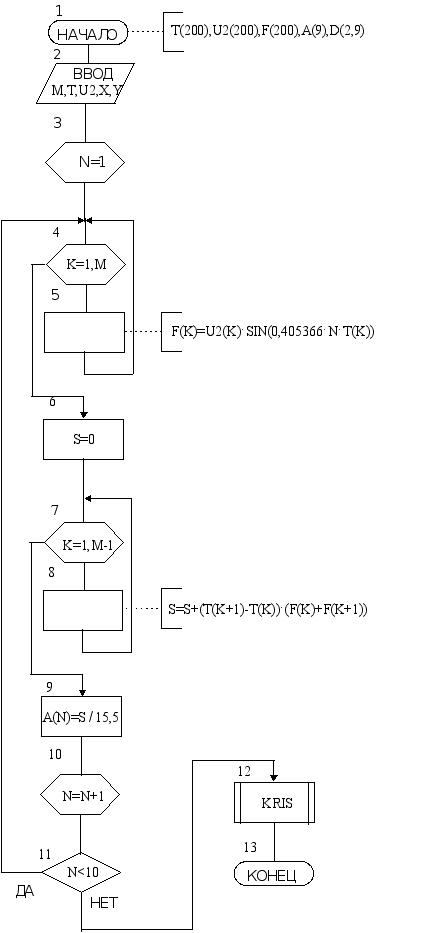
Рисунок 10
6.3Результаты гармонического анализаЗависимость амплитуды гармоники от ее номера приведены в таблицах 11, 12 и на рисунке 11.
Таблица 11
1 .284373E+01
2 .222451E-02
3 .103735E-01
4 .498333E-03
5 -.751302E-02
6 .191248E-03
7 .318412E-02
8 -.107523E-04
9 .145544E-03
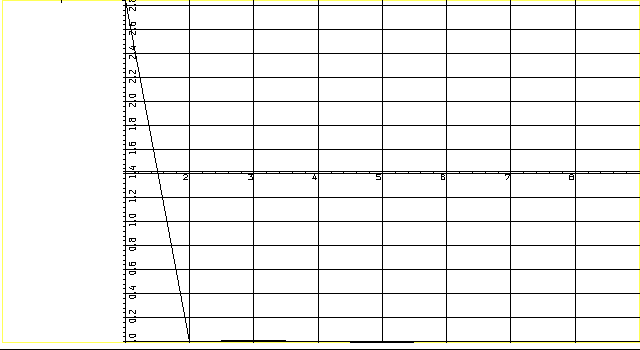
Рисунок 11
Сделаем повторное вычисление интеграла, выбрав из входной таблицы нечетные точки.
Таблица 12
1 .284373E+01
2 .222451E-02
3 .103735E-01
4 .498333E-03
5 -.751302E-02
6 .191248E-03
7 .318412E-02
8 -.107523E-04
9 .145544E-03
Интегрирование проведено с высокой точностью, так как оба решения совпадают.
Четные гармоники практически равны нулю, а наибольшая из нечетных, - третья составляет всего 0,36% от первой. В таких условиях аппроксимация этой характеристики не имеет смысла.
7.ЛИТЕРАТУРА
Б.П. ДЕМИДОВИЧ, И.А. МАРОН, Основы вычислительной математики, «Наука», М., 1966.
Б.П. ДЕМИДОВИЧ, И.А. МАРОН, Э.З. ШУВАЛОВА, Численные методы анализа, «Наука», М., 1967.
И.С. БЕРЕЗИН, Н.П. ЖИДКОВ, Методы вычислений, Физматгиз, 1961.
Н.Н. КАЛИТКИН, Численные методы, «Наука», М., 1978.
Н.С. БАХВАЛОВ, Численные методы, «Наука», М., 1975.
Д. ХИММЕЛЬБЛАУ, Прикладное нелинейное программирование, «Мир», М., 1975.
А.А. ФЕЛЬДБАУМ, А.Д. ДУДЫКИН, А.П. МАНОВЦЕВ, Н.Н. МИРОЛЮБОВ, Теоретические основы связи и управления, Физматгиз, М., 1963.
З.С. БРИЧ, Д.В. КАПИЛЕВИЧ, Н.А. КЛЕЦКОВА, ФОРТРАН 77 для ПЭВМ ЕС, «Финансы и статистика», М., 1991.
П.В. СОЛОВЬЕВ, FORTRAN для персонального компьютера, «ARIST», М., 1991.
Г.Н. РЫБАЛЬЧЕНКО, Численные методы решения задач строительства на ЭВМ, Киев УМК ВО, 1989.
Г. Н. РЫБАЛЬЧЕНКО, Методические указания к курсовой работе по дисциплине «Основы вычислительной математики», Кривой Рог, КТУ, 1997.
Исследование RC-генератора синусоидальных колеб
Похожие работы
... 7. В выводе сравните между собой вычисленное и измеренное значение силы тока и сделайте вывод о выполнении закона Ома. Отчет по лабораторной работе № 1 Исследование цепи переменного тока. выполненной учащим…… школы «Поиск» …………………………………………………………………………………… «…..»……….. 200….г Задание 1. Предварительные расчеты и измерения Емкость конденсатора: С =……… мкФ =………´ 10-6 Ф Индуктивность ...
вает разностный сигнал постоянного тока. получаемый вычитанием сигналов постоянного тока 1-го и П-го каналов радиолокатора; Эти сигналы подается на стрелочные приборы; - вырабатывает разностные импульсные сигналы, получаемые вычитанием видеосигналов 1-го и П-го каналов радиолокатора; эти разностные сигналы подавтся на индикаторы ИКО/ИДВ и на индикатор типа "и". В плате ...
... – объекты, в которых регулируется расход жидкости или газа. Методы графического определения времени разгона Та для многоемкостных ОР приведены на рис. 5 и 6. Импульсные характеристики объектов регулирования Длительное и значительное по величине воздействие, которое приходится наносить для получения разгонных характеристик объекта регулирования, вызывает длительные изменение режима его работы ...
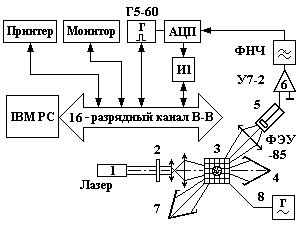
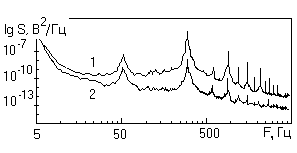
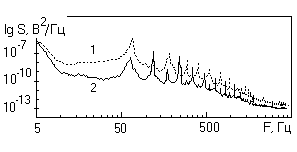
... наиболее полно использовать математические методы теории случайных процессов. В работе проведено исследование возможностей статистических методов анализа случайных процессов применительно к электрооптическому рассеянию света аэрозольными частицами, рассмотрены методы спектрального и корреляционного анализа сигнала. Твердые аэрозольные частицы неправильной формы, взвешенные в воздухе, находятся в ...
0 комментариев