Навигация
Методы кластерного анализа
1.3. Методы кластерного анализа.
Сегодня существует достаточно много методов кластерного анализа. Остановимся на некоторых из них (ниже приводимые методы принято называть методами минимальной дисперсии).
Пусть Х - матрица наблюдений: Х = (Х1, Х2,..., Хu) и квадрат евклидова расстояния между Х и Хj определяется по формуле:
![]()
1) Метод полных связей.
Суть данного метода в том, что два объекта, принадлежащих одной и той же группе (кластеру), имеют коэффициент сходства, который меньше некоторого порогового значения S. В терминах евклидова расстояния d это означает, что расстояние между двумя точками (объектами) кластера не должно превышать некоторого порогового значения h. Таким образом, h определяет максимально допустимый диаметр подмножества, образующего кластер.
2) Метод максимального локального расстояния.
Каждый объект рассматривается как одноточечный кластер. Объекты группируются по следующему правилу: два кластера объединяются, если максимальное расстояние между точками одного кластера и точками другого минимально. Процедура состоит из n - 1 шагов и результатом являются разбиения, которые совпадают со всевозможными разбиениями в предыдущем методе для любых пороговых значений.
3) Метод Ворда.
В этом методе в качестве целевой функции применяют внутригрупповую сумму квадратов отклонений, которая есть ни что иное, как сумма квадратов расстояний между каждой точкой (объектом) и средней по кластеру, содержащему этот объект. На каждом шаге объединяются такие два кластера, которые приводят к минимальному увеличению целевой функции, т.е. внутригрупповой суммы квадратов. Этот метод направлен на объединение близко расположенных кластеров.
4) Центроидный метод.
Расстояние между двумя кластерами определяется как евклидово расстояние между центрами (средними) этих кластеров:
d2ij = (X –Y)Т(X –Y) Кластеризация идет поэтапно на каждом из n–1 шагов объединяют два кластера G и , имеющие минимальное значение d2ij Если n1 много большеn2, то центры объединения двух кластеров близки друг к другу и характеристики второго кластера при объединении кластеров практически игнорируются. Иногда этот метод иногда называют еще методом взвешенных групп.
1.4 Алгоритм последовательной кластеризации.
Рассмотрим Ι = (Ι1, Ι2, … Ιn) как множество кластеров {Ι1}, {Ι2},…{Ιn}. Выберем два из них, например, Ι и Ι j, которые в некотором смысле более близки друг к другу и объединим их в один кластер. Новое множество кластеров, состоящее уже из n-1 кластеров, будет:
{Ι1}, {Ι2}…, {Ι , Ι j}, …, {Ιn}.
Повторяя процесс, получим последовательные множества кластеров, состоящие из (n-2), (n-3), (n–4) и т.д. кластеров. В конце процедуры можно получить кластер, состоящий из n объектов и совпадающий с первоначальным множеством Ι = (Ι1, Ι2, … Ιn).
В качестве меры расстояния возьмем квадрат евклидовой метрики d j2. и вычислим матрицу D = {di j2}, где di j2 - квадрат расстояния между
Ι и Ι j:
| Ι1 | Ι2 | Ι3 | …. | Ιn | |
| Ι1 | 0 | d122 | d132 | …. | d1n2 |
| Ι2 | 0 | d232 | …. | d2n2 | |
| Ι3 | 0 | …. | d3n2 | ||
| …. | …. | …. | |||
| Ιn | 0 |
Пусть расстояние между Ιi и Ιj будет минимальным:
d j2 = min {di j2, i j}. Образуем с помощью Ιi и Ιj новый кластер
{Ιi , Ι j}. Построим новую ((n-1), (n-1)) матрицу расстояния
| {Ιi , Ι j} | Ι1 | Ι2 | Ι3 | …. | Ιn | |
| {Ιi ; Ι j} | 0 | di j21 | di j22 | di j23 | …. | di j2n |
| Ι1 | 0 | d122 | d13 | …. | d12n | |
| Ι2 | 0 | di j21 | …. | d2n | ||
| Ι3 | 0 | …. | d3n | |||
| Ιn | 0 |
(n-2) строки для последней матрицы взяты из предыдущей, а первая строка вычислена заново. Вычисления могут быть сведены к минимуму, если удастся выразить di j2k,k = 1, 2,…, n; (k i j) через элементы первоначальной матрицы.
Исходно определено расстояние лишь между одноэлементными кластерами, но надо определять расстояния и между кластерами, содержащими более чем один элемент. Это можно сделать различными способами, и в зависимости от выбранного способа мы получают алгоритмы кластер анализа с различными свойствами. Можно, например, положить расстояние между кластером i + j и некоторым другим кластером k, равным среднему арифметическому из расстояний между кластерами i и k и кластерами j и k:
di+j,k = Ѕ (di k + dj k).
Но можно также определить di+j,k как минимальное из этих двух расстояний:
di+j,k = min (di k + dj k).
Таким образом, описан первый шаг работы агломеративного иерархического алгоритма. Последующие шаги аналогичны.
Довольно широкий класс алгоритмов может быть получен, если для перерасчета расстояний использовать следующую общую формулу:
di+j,k = A(w) min(dikdjk) + B(w) max(dik djk), где
A(w) = 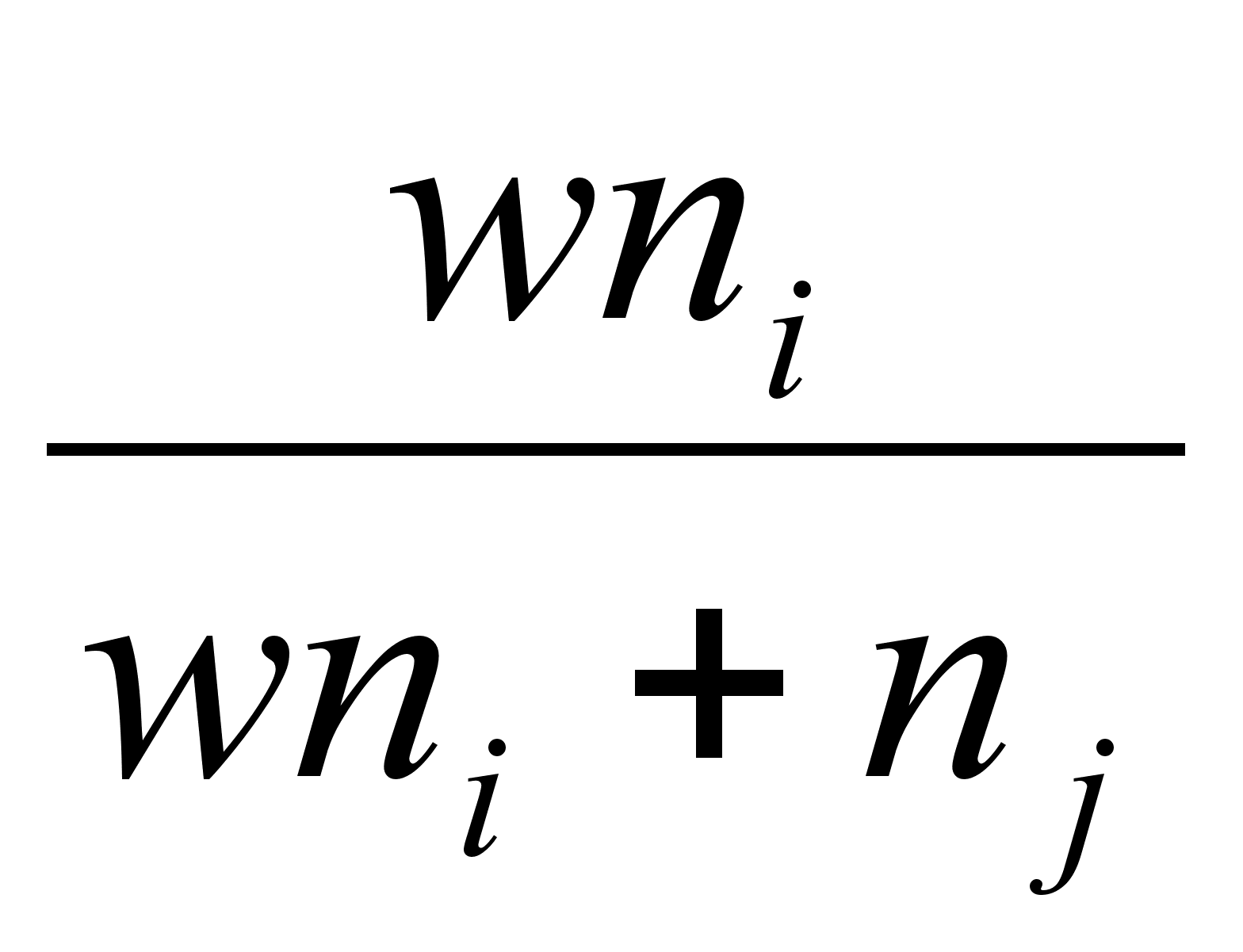 ,
если
dik
djk
,
если
dik
djk
A(w) = 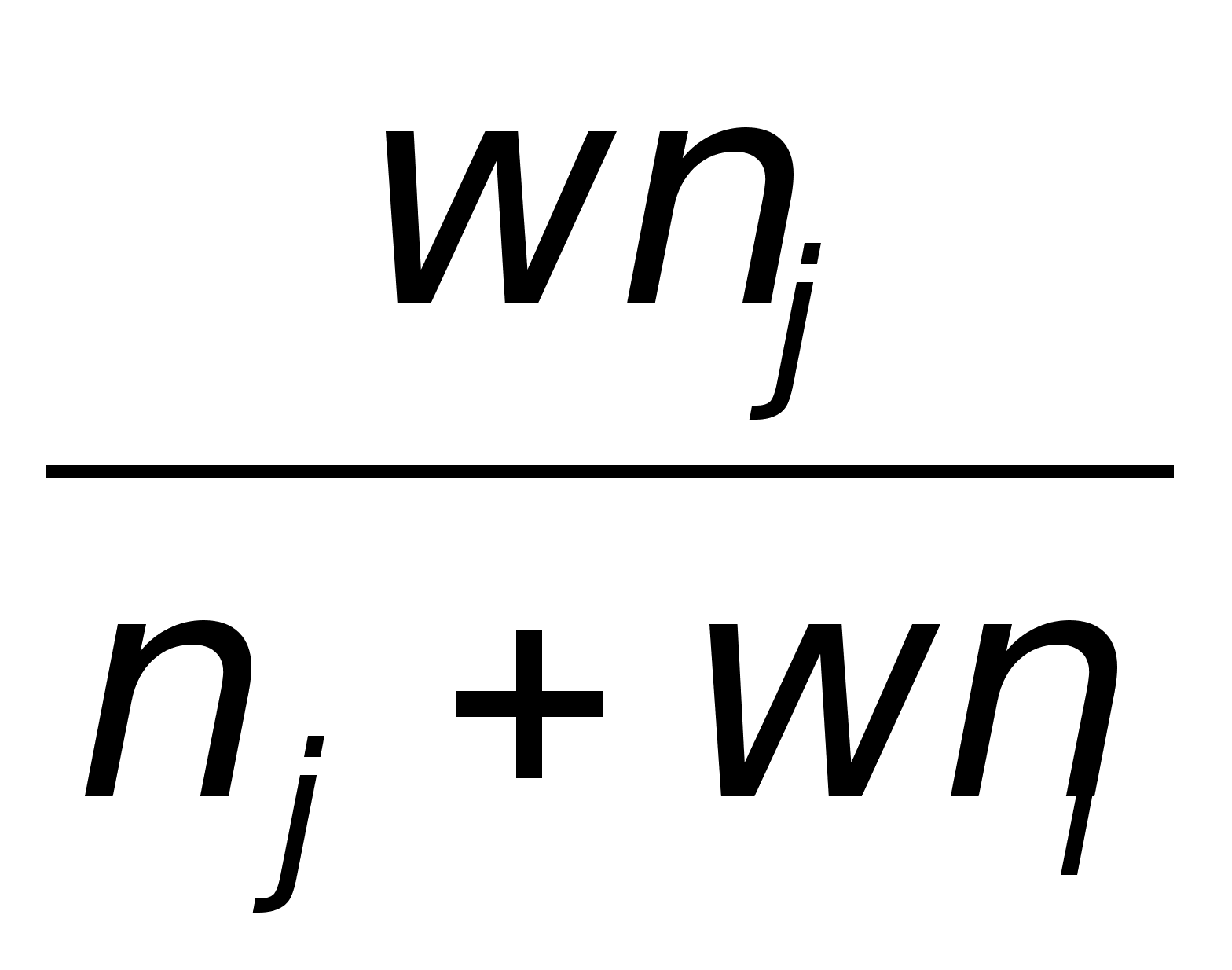 ,
если
dik
djk
,
если
dik
djk
B(w) =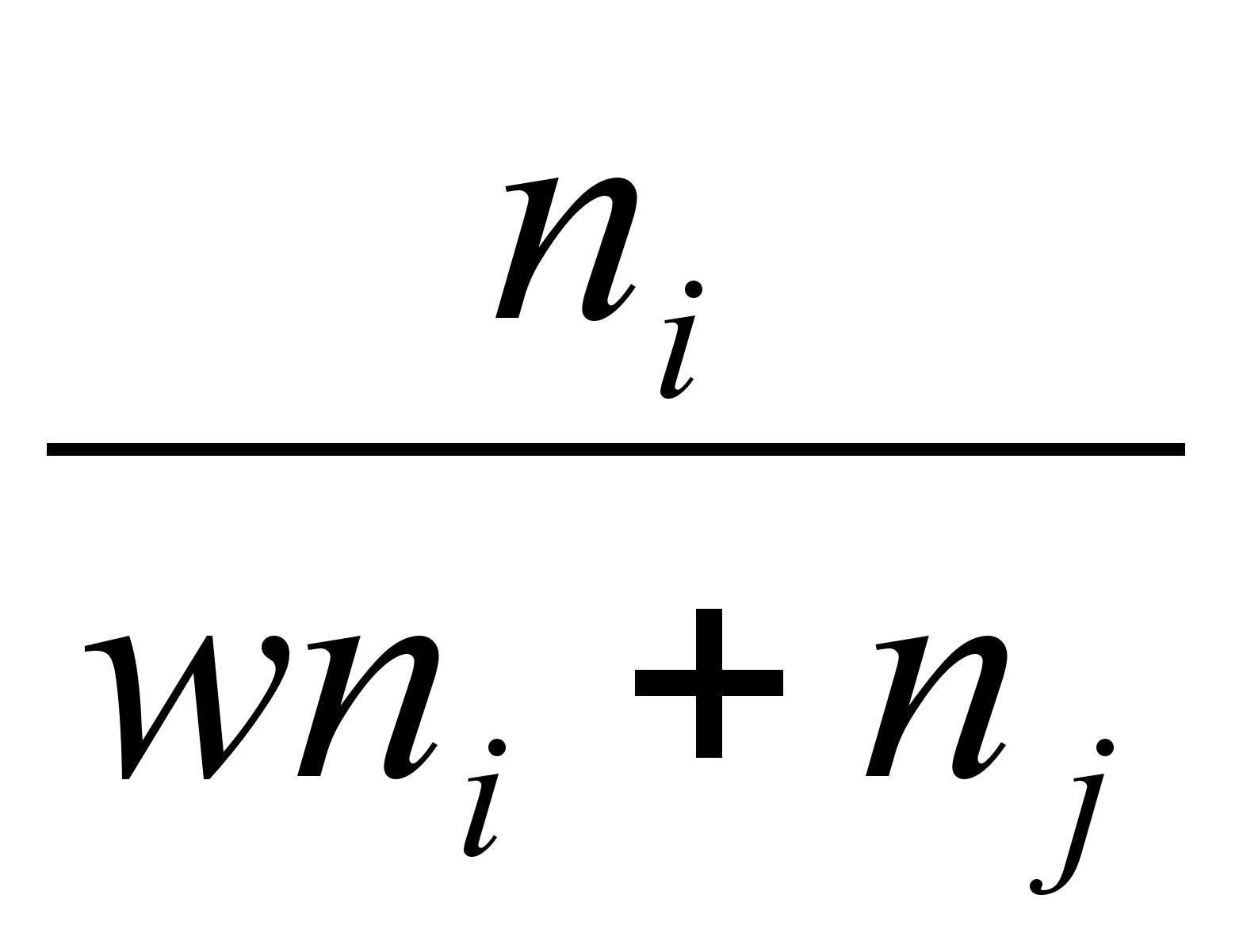 ,
если dk
djk
,
если dk
djk
B(w) = 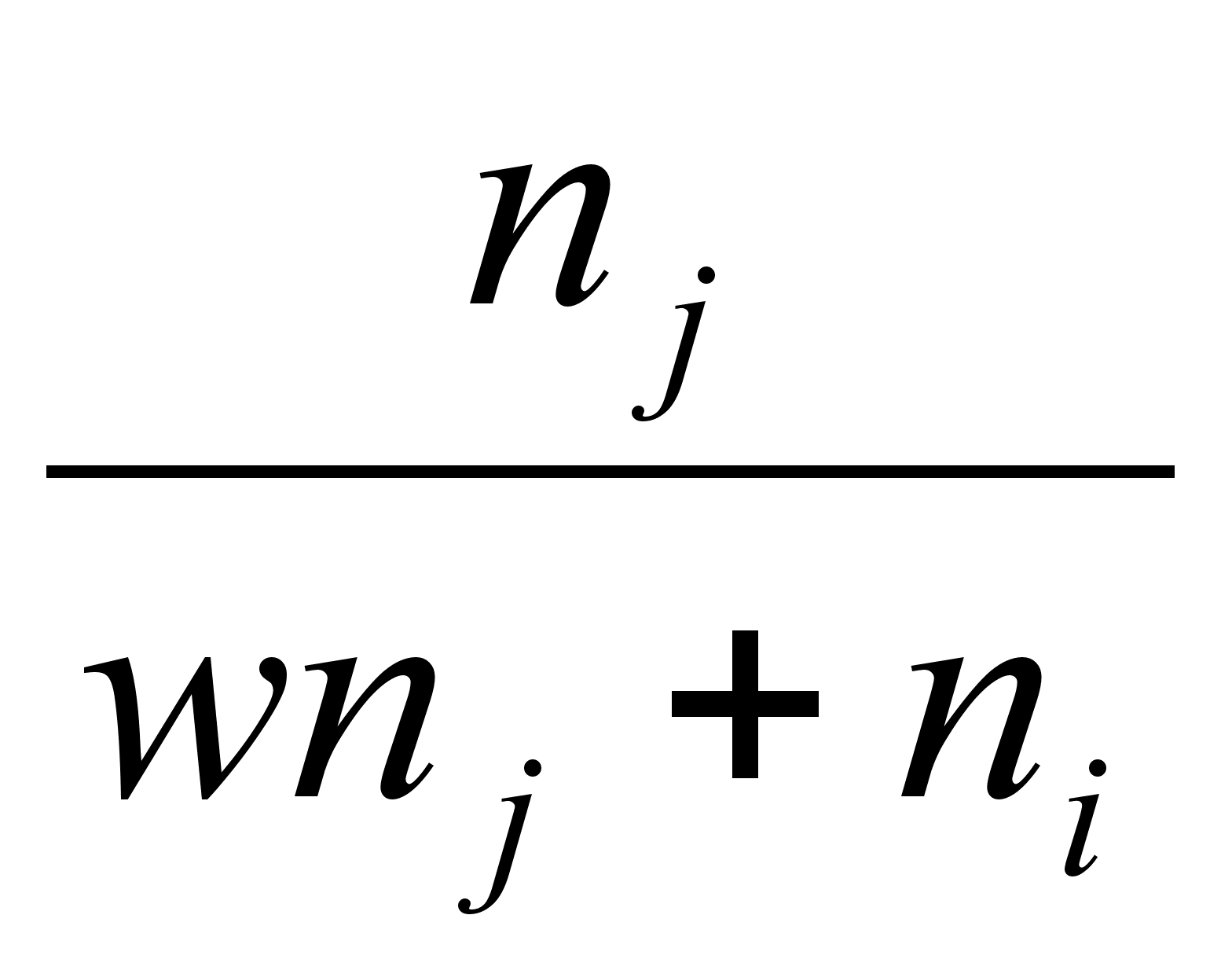 ,
если
dik djk
,
если
dik djk
где ni и nj - число элементов в кластерах i и j, а w – свободный параметр, выбор которого определяет конкретный алгоритм. Например, при w = 1 мы получаем, так называемый, алгоритм «средней связи», для которого формула перерасчета расстояний принимает вид:
di+j,k
= 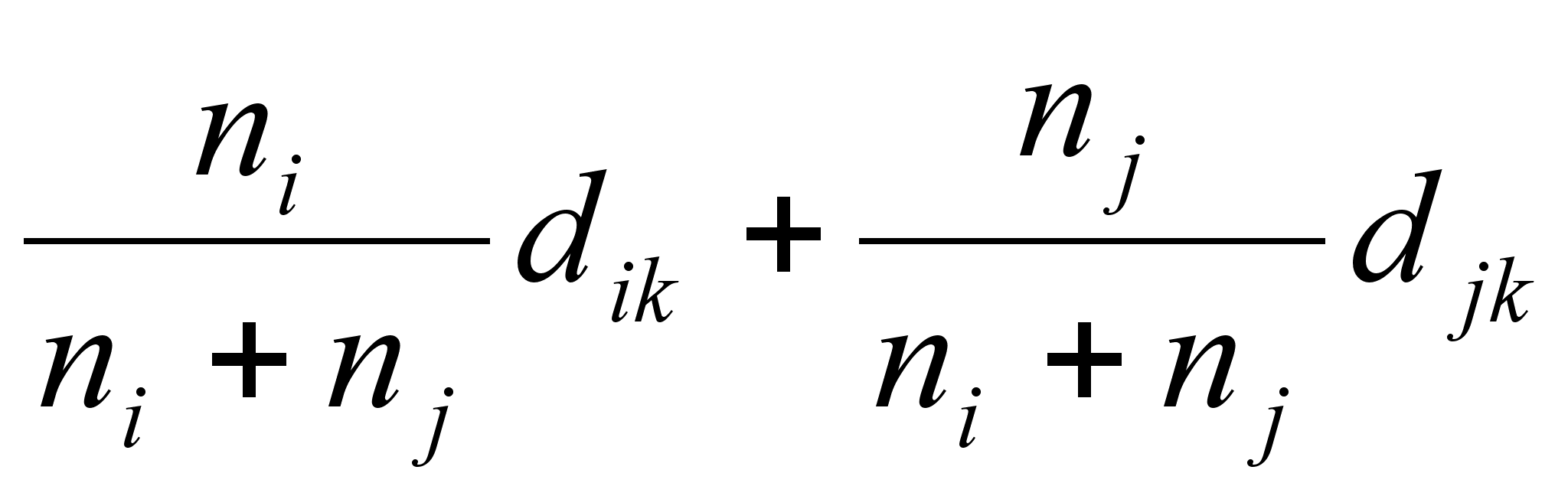
В данном случае расстояние между двумя кластерами на каждом шаге работы алгоритма оказывается равным среднему арифметическому из расстояний между всеми такими парами элементов, что один элемент пары принадлежит к одному кластеру, другой - к другому.
Наглядный смысл параметра w становится понятным, если положить w . Формула пересчета расстояний принимает вид:
di+j,k = min (d,k djk)
Это будет так называемый алгоритм «ближайшего соседа», позволяющий выделять кластеры сколь угодно сложной формы при условии, что различные части таких кластеров соединены цепочками близких друг к другу элементов. В данном случае расстояние между двумя кластерами на каждом шаге работы алгоритма оказывается равным расстоянию между двумя самыми близкими элементами, принадлежащими к этим двум кластерам.
Довольно часто предполагают, что первоначальные расстояния (различия) между группируемыми элементами заданы. В некоторых задачах это действительно так. Однако, задаются только объекты и их характеристики и матрицу расстояний строят исходя из этих данных. В зависимости от того, вычисляются ли расстояния между объектами или между характеристиками объектов, используются разные способы.
В случае кластер анализа объектов наиболее часто мерой различия служит либо квадрат евклидова расстояния
![]()
(где xih, xjh - значения h-го признака для i-го и j-го объектов, а m - число характеристик), либо само евклидово расстояние. Если признакам приписывается разный вес, то эти веса можно учесть при вычислении расстояния
![]()
Иногда в качестве меры различия используется расстояние, вычисляемое по формуле:
![]()
которые называют: "хэмминговым", "манхэттенским" или "сити-блок" расстоянием.
Естественной мерой сходства характеристик объектов во многих задачах является коэффициент корреляции между ними
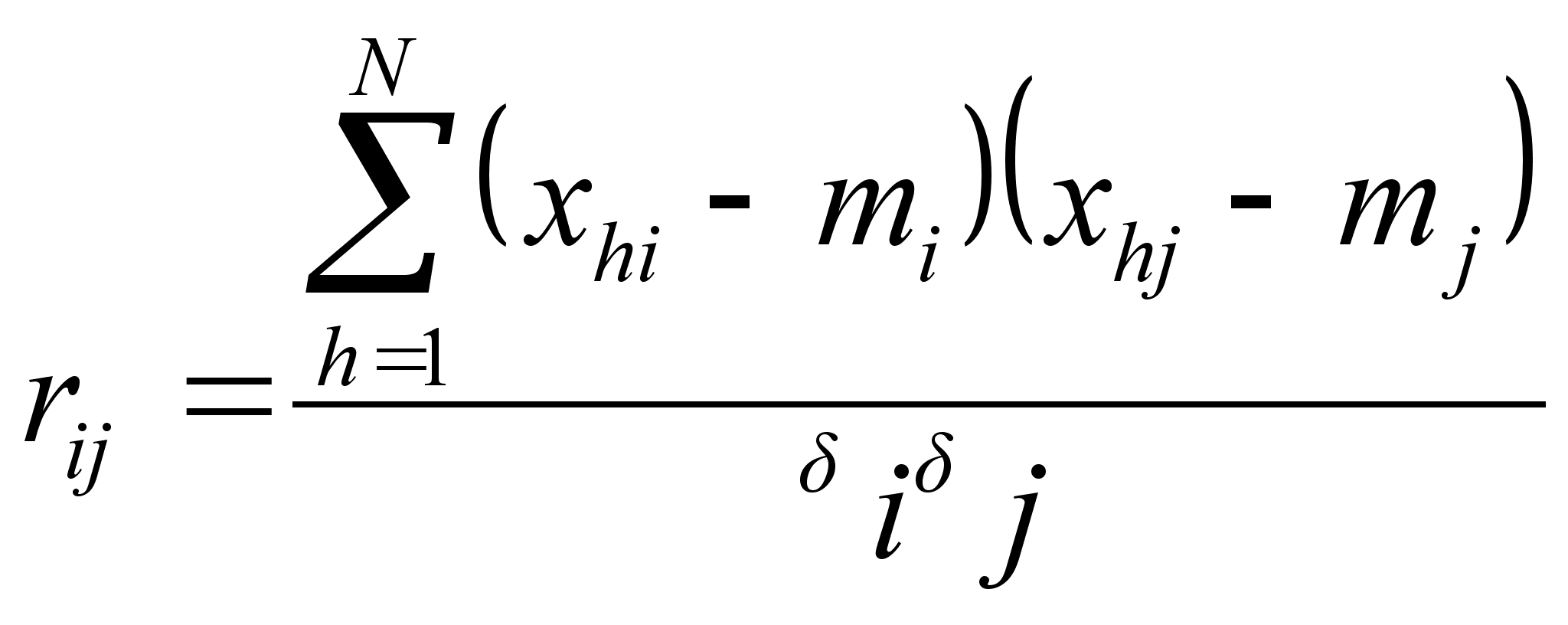
где mi ,mj ,i ,j - соответственно средние и среднеквадратичные отклонения для характеристик i и j. Мерой различия между характеристиками может служить величина 1 - r. В некоторых задачах знак коэффициента корреляции несуществен и зависит лишь от выбора единицы измерения. В этом случае в качестве меры различия между характеристиками используется 1 - ri j
Похожие работы
... предварительно нормируются, т.е. выражаются через отношение этих значений к некоторой величине, отражающей определенные свойства данного показателя. Нормирование исходных данных для кластерного анализа иногда проводится посредством деления исходных величин на среднеквадратичное отклонение соответствующих показателей. Другой способ сводиться к вычислению, так называемого, стандартизованного вклада ...
... пятого кластера стали Санкт-Петербург, Свердловская область. А вот шестой кластер состоит лишь из одного региона России- Республики Ингушетии. Для создания качественного представления о социально-экономическом положении (различиях в имущественном обеспечении и неравенстве в доходах) очень полезно будет рассмотреть таблицу окончательных кластерных центров. Таблица 9 «Окончательные кластерные ...
... . Работа имеет три раздела: В первой главе характеризируются и рассматриваются основные принципы анализа капиталовложений. Вторая глава представляет собой анализ эффективности инвестиционных проектов. Третья глава состоит из рассмотрения проблем оптимизации капиталовложений. РАЗДЕЛ 1. ОСНОВНЫЕ ПРИНЦИПЫ АНАЛИЗА ИНВЕСТИЦИОННЫХ ПРОЕКТОВ 1.1. Характеристика видов инвестиционных проектов ...
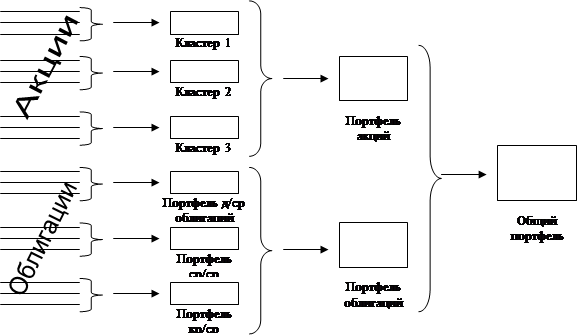
... играет большую роль. Как правило, данные нормализуют вычитанием среднего и делением на стандартное отклонение, так что дисперсия оказывается равной единице. 2. Кластерный анализ в портфельном инвестировании Общеизвестно, что изменение курсовой стоимости и дивидендов различных ценных бумаг не только в России, но и во всем ...

0 комментариев