Навигация
Имеет один корень, если a = 0
1. имеет один корень, если a = 0.
2. имеет два действительных корня Z1,2=![]() , если a > 0.
, если a > 0.
3. не имеет действительных корней, если a < 0. Но имеет два комплексных корня.
Запишем число a в виде a = (– 1)×(– a) = i2×![]() = i2×(
= i2×(![]() )2. Тогда уравнение Z2 = a запишется в виде:
Z2 – i2×(
)2. Тогда уравнение Z2 = a запишется в виде:
Z2 – i2×(![]() )2 = 0
)2 = 0
т.е.
(Z – i×![]() )(Z + i×
)(Z + i×![]() ) = 0
) = 0
Следовательно, уравнение имеет два корня: Z1,2 = ![]() i×
i×![]()
Введенное понятие корня из отрицательного числа позволяет записать корни любого квадратного уравнения с действительными коэффициентами
a×Z2 + b×Z + c = 0
По известной общей формуле
Z1,2=![]() (10)
(10)
Итак, при любых действительных a(a![]() 0), b, c корни уравнения можно находить по формуле 10. При это если дискриминант, т.е. подкоренное выражение в формуле 10
0), b, c корни уравнения можно находить по формуле 10. При это если дискриминант, т.е. подкоренное выражение в формуле 10
D = b2 – 4×a×c
положителен , то уравнение a×Z2 + b×Z + c = 0 два действительных различных корня. Если D = 0, то уравнение a×Z2 + b×Z + c = 0 имеет один корень. Если D < 0, то уравнение a×Z2 + b×Z + c = 0 имеет два различных комплексных корня.
Комплексные корни квадратного уравнения обладают такими же свойствами, как и известные нам свойства действительных корней.
Сформулируем основные из них:
Пусть Z1,Z2 – корни квадратного уравнения a×Z2 + b×Z + c = 0, a![]() 0. Тогда справедливы свойства:
0. Тогда справедливы свойства:
1. Теорема Виета: Z1 + Z2 = –![]()
Z1×Z2 = ![]()
2. При всех комплексных Z справедлива формула
a×Z2 + b×Z + c = a×(Z – Z1)×(Z – Z2)
Пример 5:
Z2 – 6·Z + 10 = 0
Д = b2 – 4·a·c
Д = 62 – 4·10 = – 4
– 4 = i2·4
Z1,2 = 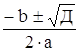
Z1,2 =![]()
Ответ: Z1 = Z2 = 3 + i
Пример 6:
3·Z2 +2·Z + 1 = 0
Д = b2 – 4·a·c
Д = 4 – 12 = – 8
Д = –1·8 = 8·i2
Z1,2 = 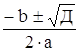 =
= 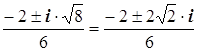
Z1,2 =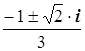
Z1 = – (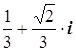 )
)
Z2 = –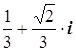
Ответ: Z1 = Z2 = –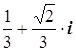
Пример 7:
Z4 – 8·Z2 – 9 = 0
Z2 = t
t2 – 8·t – 9 = 0
Д = b2 – 4·a·c = 64 + 36 = 100
t1,2 = 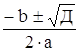 =
= ![]() = 4
= 4![]()
t1 = 9 t2 = – 1
Z2 = 9 Z2 = – 1
Z1,2 =![]() 3 Z =
3 Z = ![]()
Z3,4 =![]() i
i
Ответ: Z1,2 =![]() 3, Z3,4 =
3, Z3,4 =![]() i
i
Пример 8:
Z4 + 2·Z2 – 15 = 0
Z2 = t
t2 + 2·t – 15 = 0
Д = b2 – 4·a·c = 4 + 60 = 64
t1,2 = 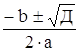 =
= ![]() = –1
= –1![]() 4
4
t1 = – 5 t2 = 3
Z2 = – 5 Z2 = 3
Z2 = – 1·5 Z3,4 =![]()
![]()
Z2 = i2·5
Z1,2 =![]() i
i![]()
Ответ: Z1,2 =![]() i
i![]() , Z3,4 =
, Z3,4 =![]()
![]()
Пример 9:
Z2 = 24 – 10·i
Пусть Z = X + Y·i
(X + Y·i)2 = X2 + 2·X·Y·i –Y2
X2 + 2·X·Y·i – Y2 = 24 – 10·i
|
|
Y = – ![]()
X2 – ![]() = 24
= 24
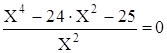 умножим на X2
умножим на X2![]() 0
0
X4 – 24·X2 – 25 = 0
X2 = t
t2 – 24·t – 25 = 0
t1·t2 = – 25
t1 + t2 = 24
t1 = 25 t2 = – 1
X2 = 25 X2 = – 1 — нет решений
X1,2 = ![]() 5
5
X1 = 5 X2 = – 5
Y1 = – ![]() Y2 =
Y2 = ![]()
Y1 = – 1 Y2 = 1
Тогда:
Z1,2 =![]() (5 – i)
(5 – i)
Ответ: Z1,2 =![]() (5 – i)
(5 – i)
ЗАДАЧИ:
|
|
| |
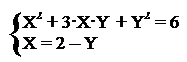
( 2 – Y)2 + 3·( 2 – Y)·Y + Y2 = 6
4 – 4·Y + Y2 + 6·Y – 3·Y2 + Y2 = 6
–Y2 + 2Y – 2 = 0 /–1
Y2 – 2Y + 2 = 0
Д = b2 – 4·a·c = 4 – 8 = – 4
– 4 = – 1·4 = 4· i2
Y1,2 = 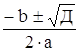 =
= ![]() = 1
= 1![]() i
i
Y1 = 1– i Y2 = 1 + i
|
Ответ: {1 + i ; 1– i}
{1– i ; 1 + i}
|
|
|
|
— Возведем в квадрат
— Возведем в куб
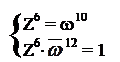
w10×![]() 12 = 1
12 = 1
w10×![]() 10 ×
10 ×![]() 2 = 1
2 = 1
(w×![]() )10×
)10×![]() 2 = 1
2 = 1
(![]() )10×
)10×![]() 2 = 1
2 = 1
т.к. w = A + B×i
![]() = A – B×i
= A – B×i
w×![]() = (A + B×i)·( A – B×i) = A2 – (B×i)2 = A2 + B2 =
= (A + B×i)·( A – B×i) = A2 – (B×i)2 = A2 + B2 = ![]() 2 = w×
2 = w×![]()
т.е. ![]() 20·
20·![]() 2 = 1
2 = 1
Возьмем модуль от обоих частей последнего уравнения:
![]() 20·
20·![]() 2 = 1
2 = 1
![]() 22 = 1
22 = 1
т.е.
![]() = 1
= 1
Тогда из уравнения получим
![]() 2 = 1
2 = 1
т.е.
![]() =
= ![]() 1
1
w1 = 1 w2 = –1
Подставим эти значения в первое уравнение данной системы и найдем численное значение Z
1) w1 = 1
Z6 = 1
1 = 1·( cos(2pk) + i·sin(2pk)), kÎZ
Z = r×(cosj + i×sinj)
r6×(cos6j + i×sin6j) = cos(2pk) + i·sin(2pk), kÎZ
r6 = 1 6j = 2pk
r = 1 j = ![]() , kÎZ
, kÎZ
Z = cos![]() + i·sin
+ i·sin![]() , kÎZ
, kÎZ
k = 0,1,2...
k = 0
Z1 = cos0+ i×sin0 = 1 + 0 = 1
Z1 = 1
k = 1
Z2 = cos![]() + i·sin
+ i·sin![]() =
= 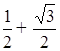 i =
i = 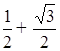 i
i
Z2 =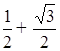 i
i
k = 2
Z3 = cos![]() + i·sin
+ i·sin![]() = –
= –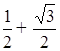 i
i
Z3 = –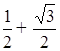 i
i
k = 3
Z4 = cosp + i·sinp = –1 + 0 = –1
Z4 = –1
k = 4
Z5 = cos![]() + i·sin
+ i·sin![]() = –
= –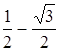 i
i
Z5 = –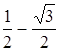 i
i
k = 5
Z6 = cos![]() + i·sin
+ i·sin![]() =
= 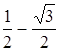 i
i
Z6 = 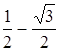 i
i
Ответ: Z1 = 1, Z2 =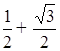 i, Z3 = –
i, Z3 = –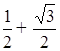 i, Z4 = –1, Z5 = –
i, Z4 = –1, Z5 = –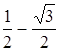 i, Z6 =
i, Z6 = 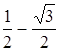 i
i
2) w2 = –1
Z6 = –1
–1 = 1·( cos(p + 2pk) + i·sin(p + 2pk)), kÎZ
Пусть Z = r×(cosj + i×sinj), тогда данное уравнение запишется в виде:
r6×(cos6j + i×sin6j) = cos(p + 2pk) + i·sin(p + 2pk), kÎZ
r6 = 1 6j = p + 2pk
r = 1 j = ![]() , kÎZ
, kÎZ
Z = cos(![]() ) + i·sin(
) + i·sin(![]() ), kÎZ
), kÎZ
k = 0,1,2...
k = 0
Z1 = cos![]() + i·sin
+ i·sin![]() =
= 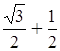 i
i
Z1 =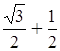 i
i
k = 1
Z2 = cos(![]() ) + i·sin(
) + i·sin(![]() ) = 0 + i = i
) = 0 + i = i
Z2 = i
k = 2
Z3 = cos(![]() ) + i·sin(
) + i·sin(![]() ) = –
) = –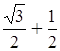 i
i
Z3 = –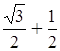 i
i
k = 3
Z4 = cos(![]() ) + i·sin(
) + i·sin(![]() ) = –
) = –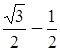 i
i
Z4 = –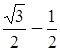 i
i
k = 4
Z5 = cos(![]() ) + i·sin(
) + i·sin(![]() ) = 0 – i = – i
) = 0 – i = – i
Z5 = – i
k = 5
Z6 = cos(![]() ) + i·sin(
) + i·sin(![]() ) =
) = 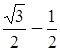 i
i
Z6 =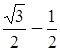 i
i
Ответ: Z1 =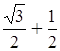 i , Z2 = i, Z3 = –
i , Z2 = i, Z3 = –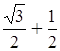 i , Z4 = –
i , Z4 = –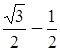 i, Z5 = – i, Z6 =
i, Z5 = – i, Z6 =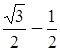 i
i
3)
Доказать, что сумма двух комплексных чисел не превосходит сумму модулей этих чисел.
1 СПОСОБ:
Пусть Z1=X+Y×i и Z2=U+V×i
Доказать что:
![]()
![]()
Предположим противоположное:
![]() >
>![]() / т.к. корень существует только из неотрицательного числа, то можно возвести в квадрат обе части неравенства.
/ т.к. корень существует только из неотрицательного числа, то можно возвести в квадрат обе части неравенства.
X2+2·X·U+U2+Y2+2·Y·V+V2
> X2+Y2+U2+V2+2·![]()
2·(X·U+Y·V) > 2·![]()
Если мы предположили верно, то X·U+Y·V > 0, а поэтому возведем в квадрат:
X2·U2+2·XU·Y·V+Y2·V2 > X2·U2 + X2·V2+Y2·U2+Y2·V2
2·X·Y·V·U > X2·V2+Y2·U2
X2·V2+Y2·U2 – 2·X·Y·V·U < 0
(X·V + Y·U)2 < 0
Это невозможно, т.к. A2![]() 0, значит полученное нами неравенство неверно.
0, значит полученное нами неравенство неверно.
![]()
что и требовалось доказать
2 СПОСОБ:
|
|
Пусть Z1 и Z2– два произвольных комплексных числа. Z1– соответствует точке A, Z2– соответствует точке B.
В силу неравенства треугольника
![]() т.е.
т.е.
![]()
Что и требовалось доказать.
[S1]
Похожие работы
... и ЭДС. В расчёте можно оперировать и действующими значениями величин – ; ; . Символический метод, основанный на изображении векторов комплексными числами введён Штейнмецом, у нас развит ?????????. Связь комплексных амплитуд тока и напряжения в пассивных элементах электрической цепи Законы Кирхгофа для токов и напряжений, представленных комплексными амплитудами ...
... учащихся, школьную документацию, сделать выводы о степени усвоения данного понятия. Подвести итог об исследовании особенностей математического мышления и процесса формирования понятия комплексного числа. Описание методов. Диагностические: I этап. Беседа проводилась с учителем математики, которая в 10Є классе преподает алгебру и геометрию. Беседа состоялась по истечении некоторого времени с начала ...
... 1. Точки М и N — середины диагоналей АС и BD четырехугольника ABCD. (Рис.1)Доказать, что |AB|2+|BC|2+|CD|2+|DA|2 = |AC|2+|BD|2+4|MN|2.Решение. Пусть точкам A, В, С, D, М, N соответствуют комплексные числа а, b, с, d, т, п.Так как m = и n = , то |AB|2+|BC|2+|CD|2+|DA|2 |AC|2+|BD|2+4|MN|2 .Равенство доказано.Задача 2. Доказать, что если в плоскости параллелограмма ABCD существует такая точка М, ...
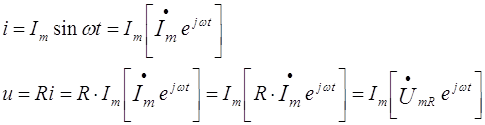
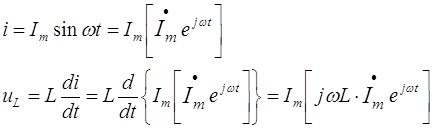
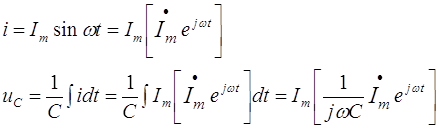
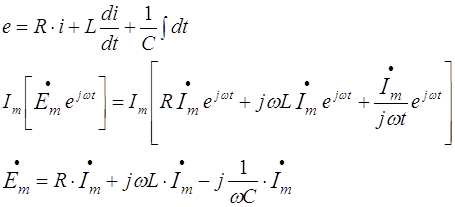
0 комментариев