Навигация
События А и В называются несовместными, если А ∩ В = Æ
1. События А и В называются несовместными, если А ∩ В = Æ.
2. События А1, А2 , … Аn называются попарно несовместными, если для любых i ≠ j, 1 £ i,j £ n, события Аiи Аj несовместны.
3. Говорят, что событие А влечет событие В, и пишут А Í В, если всегда, как только происходит событие А, происходит и событие В. На языке теории множеств это означает, что любой элементарный исход, входящий в А, одновременно входит и в событие В.
Вероятность на дискретном пространстве элементарных исходовПредположим, что мы имеем дело с дискретным пространством элементарных исходов, то есть пространством, состоящим из конечного или счетного числа элементов:
Ω = {ω1, ω2 , … ωn , … }.
Определение 6. Поставим каждому элементарному исходу ωi Î Ω в соответствие число p(ωi ) Î [0,1] так, что
Назовем число p(ωi) вероятностью элементарного исхода ωi . Вероятностью события А Í Ω называется число
равное сумме вероятностей элементарных исходов, входящих в множество А.
Замечание 4. Позднее, познакомившись с аксиоматикой теории вероятностей, мы зададим вероятности событий непосредственно, а не через вероятности элементарных исходов. Тем более, что сложением вероятностей элементарных исходов можно получить лишь вероятность события, состоящего не более чем из счетного числа элементарных исходов (иначе само понятие суммирования не определено). Но на дискретном пространстве элементарных исходов определить вероятности событий так, как это сделано в определении 6, всегда возможно.
Перечислим очевидные в случае дискретного пространства элементарных исходов свойства вероятности, которые мы скоро докажем сразу в общем случае.
1. 0 £ Р(А) £ 1;
2. Р(Ω) = 1;
3. Р(Æ) = 0;
4. Р(Ō) = 1 - Р(О);
5. если А и В несовместны, то Р(А U В) = Р(А) + Р(В);
6. в общем же случае Р(А U В) = Р(А) + Р(В) - Р(А ∩ В);
7. если А Í В, то Р(А) £ Р(В).
Классическое определение вероятностиПредположим, что мы имеем дело с пространством элементарных исходов, состоящим из конечного числа N элементов: Ω = {ω1, ω2, … ωN}. Более того, предположим, что из каких-либо соображений мы можем считать элементарные исходы равновозможными. Тогда вероятность любого из них принимается равной 1/ N.
Эти соображения чаще всего не имеют отношения к математической модели и основаны на какой-либо симметрии в эксперименте (симметричная монета, хорошо перемешанная колода карт, правильная кость). Либо мы можем заранее считать исходы эксперимента равновозможными, но тогда рано или поздно все равно возникнет вопрос о соответствии такой математической модели реальному эксперименту.
Если событие А = {![]() } состоит из k элементарных исходов, то вероятность этого события равняется
} состоит из k элементарных исходов, то вероятность этого события равняется
![]()
отношению k / N:
где символом │А│ обозначено число элементов конечного множества А.
Определение 7.
Говорят, что эксперимент удовлетворяет классическому определению вероятности (или классической вероятностной схеме), если пространство элементарных исходов состоит из конечного числа │А│ = N равновозможных исходов.
В этом случае вероятность любого события А вычисляется по формуле
называемой классическим определением вероятности. Эта формула читается так: «вероятность события А равна отношению числа исходов, благоприятствующих событию А, к общему числу исходов».
Замечание 5. Полезно помнить классическую формулировку Якоба Бернулли: «Вероятность есть степень достоверности и отличается от нее как часть от целого». (Ars Conjectandi, 1713 г.)
Замечание 6. Мы видим теперь, что подсчет вероятности в классической схеме сводится к подсчету числа «шансов» (элементарных исходов), благоприятствующих какому-либо событию, и общего числа шансов. Как правило, это делается с помощью формул комбинаторики.
Рассмотрим описанные в параграфе 1.1 урновые схемы. Напомним, что речь идет об извлечении k шариков из урны, содержащей n шариков. При этом три схемы: с возвращением и с учетом порядка, без возвращения и с учетом порядка, а также без возвращения и без учета порядка удовлетворяют классическому определению вероятности.
Общее число элементарных исходов в этих схемах подсчитано в теоремах 4, 2, 3 и равно, соответственно,![]()
Четвертая же схема — схема выбора с возвращением и без учета порядка — имеет заведомо неравновозможные исходы.
Пример 6. Рассмотрим, скажем, выбор двух шариков из двух или, что то же самое, дважды подбросим монету. Если учитывать порядок, то исходов получится 4, и все они равновозможны, то есть имеют вероятность по 1/4:
(герб, герб), (решка, решка), (решка, герб), (герб, решка).
Если порядок не учитывать, то следует объявить два последних исхода одним и тем же результатом эксперимента, и получить три исхода вместо четырех: выпало два герба, либо две решки, либо один герб и одна решка.
При этом первые два исхода имеют вероятность 1/4, а последний — вероятность 1/4+1/4=1/2.
Гипергеометрическое распределениеПример 7.
 Из урны, в которой n1 белых и n-n1 чёрных шаров, наудачу, без возвращения вынимают kшаров, k<n. Термин «наудачу» означает, что появление любого набора из k шаров равно возможно. Найти вероятность того, что будет выбрано ровно k1 белых и k - k1 чёрных шаров.
Из урны, в которой n1 белых и n-n1 чёрных шаров, наудачу, без возвращения вынимают kшаров, k<n. Термин «наудачу» означает, что появление любого набора из k шаров равно возможно. Найти вероятность того, что будет выбрано ровно k1 белых и k - k1 чёрных шаров.
Заметим, что при k1 > n1 или k - k1 > n - n1 искомая вероятность равна 0, так как соответствующее событие невозможно. Пусть k1 < n1 и k - k1 < n - n1. Результатом эксперимента является набор из k шаров. При этом можно не учитывать или учитывать порядок следования шаров.
1. Выбор без учета порядка. Общее число элементарных исходов есть число k –элементных подмножеств множества, состоящего из n элементов, то есть ![]() (по теореме 3).
(по теореме 3).
Обозначим через A событие, вероятность которого требуется найти. Событию A благоприятствует появление любого набора, содержащего k1 белых шаров и k - k1 черных.
Число благоприятных исходов равно произведению (по теореме 1) числа способов выбрать k1 белых шаров из n1 и числа способов выбрать k - k1 черных шаров из n - n1:
![]()
Вероятность события A равна:
2. Выбор с учетом порядка. Общее число элементарных исходов есть число способов разместить n элементов на k местах![]() (по теореме 2).
(по теореме 2).
При подсчете числа благоприятных исходов нужно учесть, как число способов выбрать нужное число шаров, так и число способов расположить эти шары среди k. Можно, скажем, посчитать число способов выбрать k1 мест среди k (равное
В рассмотренной задаче мы сопоставили каждому набору из k1 белых и k-k1черных шаров вероятность получить этот набор при выборе k шаров из урны, содержащей n1белых и n-n1черных шаров:
Определение 8. Соответствие или следующий набор вероятностей
Называется гипергеометрическим распределением.
Раздел 2. Геометрическая вероятность 2.1 Что это такое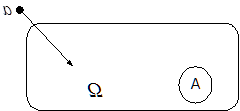 Рассмотрим какую-нибудь область Ω в Rm ,(на прямой, на плоскости, в пространстве). Предположим, что «мера» Ω (длина, площадь, объем, соответственно) конечна. Пусть случайный эксперимент состоит в том, что мы наудачу бросаем в эту область точку а. Термин «наудачу» здесь означает, что вероятность попадания точки в любую часть А Í Ω не зависит от формы или расположения А внутри Ω, а зависит лишь от «меры» области.
Рассмотрим какую-нибудь область Ω в Rm ,(на прямой, на плоскости, в пространстве). Предположим, что «мера» Ω (длина, площадь, объем, соответственно) конечна. Пусть случайный эксперимент состоит в том, что мы наудачу бросаем в эту область точку а. Термин «наудачу» здесь означает, что вероятность попадания точки в любую часть А Í Ω не зависит от формы или расположения А внутри Ω, а зависит лишь от «меры» области.
Определение 9. Эксперимент удовлетворяет условиям «геометрического определения вероятности», если его исходы можно изобразить точками некоторой области Ω в Rm так, что вероятность попадания точки в любую А Í Ω не зависит от формы или расположения А внутри Ω, а зависит лишь от меры области А (и, следовательно, пропорциональна этой мере):
«Мерой» мы пока будем называть длину, площадь, объем и т.д.
Если для точки, брошенной в область Ω, выполнены условия геометрического определения вероятности, то говорят, что точка равномерно распределена в области Ω.
Пример 8. Точка наудачу бросается на отрезок [0,1]. Вероятность точке попасть в точку {0,5} равна нулю, так как мера множества, состоящего из одной точки («длина точки»), есть 0. Вместе с тем попадание в точку {0,5} не является невозможным событием — это один из элементарных исходов эксперимента.
2.2 Задача о встречеПример 9. Два лица Х и У условились встретиться в определенном месте между двумя и тремя часами дня. Пришедший первым ждет другого в течении 10 минут, после чего уходит. Чему равна вероятность встречи этих лиц, если каждый из них может прийти в любое время в течение указанного часа независимо от другого?
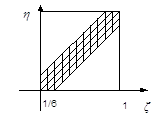 |
Будем считать интервал с 14 до 15 часов дня отрезком [0,1] длиной 1 час. Пусть ξ («кси») и η («эта») — моменты прихода Х и У (точки отрезка [0,1]).Все возможные результаты эксперимента — множество точек квадрата со стороной 1:
Ω = {( ξ , η): 0 £ ξ £1 0 £ η £1 }=[0,1]x[0,1]
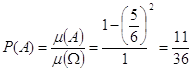 |
Можно считать, что эксперимент сводится к бросанию точки наудачу в квадрат. При этом благоприятными исходами являются точки множества A = {( ξ , η): │ξ - η│ £ 1/6 } (10 минут = 1/6 часа). То есть попадание в множество A наудачу брошенной в квадрат точки означает, что Х и У встретятся.
Тогда вероятность встреч и равна
2.3 Задача БюффонаПример 10. На плоскости начерчены параллельные прямые, находящиеся друг от друга на расстоянии 2a. На плоскость наудачу брошена игла длины 2l < 2a. Какова вероятность того, что игла пересечет одну из прямых?
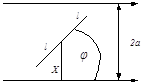 Поймем, что означает здесь «наудачу брошена игла». Возможные положения иглы (отрезка) на плоскости полностью определяются положением середины иглы и углом поворота иглы относительно какого-либо направления. Причем две эти переменные (положение центра и угол поворота) меняются независимо друг от друга. Обозначим через хÎ[0, a] расстояние от середины иглы до ближайшей прямой, а φ Î [0, π] —
Поймем, что означает здесь «наудачу брошена игла». Возможные положения иглы (отрезка) на плоскости полностью определяются положением середины иглы и углом поворота иглы относительно какого-либо направления. Причем две эти переменные (положение центра и угол поворота) меняются независимо друг от друга. Обозначим через хÎ[0, a] расстояние от середины иглы до ближайшей прямой, а φ Î [0, π] —
угол между каким-то направлением прямых и иглой. Множество возможных положений иглы целиком определяется выбором наудачу точки из прямоугольника Ω = [0,π] x [0,a]. Игла пересекает ближайшую прямую, если координаты выбранной наудачу точки удовлетворяют неравенству: х £. l sin φ
Площадь области А Í Ω, точки которой удовлетворяют такому неравенству, равна
И так как μ(Ω) = aπ, то искомая вероятность равна 2.4 Парадокс Бертрана
Пример 11 ( Josef Bertrand, “Calcul des Probabilites", 1888).
В круге единичного радиуса наудачу выбирается хорда. Какова вероятность того, что ее длина будет больше, чем длина стороны вписанного в круг правильного треугольника?
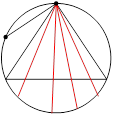 Есть по крайней мере три способа «выбрать наудачу хорду в круге». 1. Зафиксируем одну точку (конец хорды) на окружности и выберем наудачу на окружности другую точку (второй конец хорды). Здесь Ω = [0, 2π], а благоприятными являются положения второй точки на интервале [2π/3, 4π/3] (хорды, помеченные на рисунке красным цветом). Вероятность получить «длинную» хорду равна 1/3.
Есть по крайней мере три способа «выбрать наудачу хорду в круге». 1. Зафиксируем одну точку (конец хорды) на окружности и выберем наудачу на окружности другую точку (второй конец хорды). Здесь Ω = [0, 2π], а благоприятными являются положения второй точки на интервале [2π/3, 4π/3] (хорды, помеченные на рисунке красным цветом). Вероятность получить «длинную» хорду равна 1/3.
 2. Существует ровно одна хорда, для которой данная точка в круге является серединой (кроме того случая, когда брошенная наудачу точка попадет в центр круга. Но поскольку вероятность этого события равна нулю, то учет или неучет такого события не влияет на итоговую вероятность). Можно поэтому выбирать наудачу хорду, бросая наудачу точку (середину хорды) в круг. Здесь Ω — круг радиуса 1, μ(Ω) = π, а благоприятными являются положения середины хорды внутри вписанного в треугольник круга (радиусом 1/2).Вероятность получить «длинную» хорду равна отношению площадей кругов, то есть 1/4.
2. Существует ровно одна хорда, для которой данная точка в круге является серединой (кроме того случая, когда брошенная наудачу точка попадет в центр круга. Но поскольку вероятность этого события равна нулю, то учет или неучет такого события не влияет на итоговую вероятность). Можно поэтому выбирать наудачу хорду, бросая наудачу точку (середину хорды) в круг. Здесь Ω — круг радиуса 1, μ(Ω) = π, а благоприятными являются положения середины хорды внутри вписанного в треугольник круга (радиусом 1/2).Вероятность получить «длинную» хорду равна отношению площадей кругов, то есть 1/4.
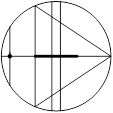
3. Наконец, можно ограничиться рассмотрением только хорд, перпендикулярных какому-либо диаметру (остальные могут быть получены поворотом). То есть эксперимент может состоять в выборе середины хорды наудачу на диаметре круга — отрезке длиной 2. Благоприятными являются положения середины хорды на отрезке длиной 1. Искомая вероятность для такого эксперимента равна 1/2.
В чем причина разницы в ответах на, казалось бы, один и тот же вопрос? На самом деле формулировка задач и не корректна с математической точки зрения. «Выбор наудачу хорды в круге» может быть по-разному описан с помощью геометрического определения вероятности (что мы и сделали). То есть этот «эксперимент» можно по-разному описать с помощью выбора наудачу точки в некоторой области.
Слово «эксперимент» взято в кавычки не напрасно: сказав «в круге наудачу выбирается хорда», мы еще не описали физического эксперимента. Действительно, каждому из трех предложенных способов выбора хорд можно сопоставить конкретный физический эксперимент (всякий раз другой).
Так что парадокс исчезает сразу, как только получен ответ на вопрос: что значит «в круге наудачу выбирается хорда»?
Заканчивая обсуждение понятия геометрической вероятности, сделаем очень важное для дальнейшего замечание.
Замечание 7. Если даже эксперимент удовлетворяет геометрическому определению вероятности, далеко не для всех множеств А Í Ω вероятность может быть вычислена как отношение меры А к мере Ω. Причиной этого является существование так называемых «неизмеримых» множеств, то есть множеств, мера которых не существует.
А если не для всех подмножеств Ω мы можем определить их вероятности, следует сузить класс множеств, называемых «событиями», оставив в этом классе только те множества, для которых мы можем определить вероятность.
В следующей главе мы займемся построением (вслед за Андреем Николаевичем Колмогоровым) аксиоматики теории вероятностей: познакомимся с понятиями σ-алгебры (или поля) событий, вероятностной меры, вероятностного пространства.
Раздел 3. Аксиоматика теории вероятностей 3.1 σ -алгебра событийПусть Ω — пространство элементарных исходов некоторого случайного эксперимента (то есть, вообще говоря, множество произвольной природы). Мы собираемся определить набор подмножеств Ω, которые будут называться событиями, и затем задать вероятность как функцию, определенную только на множестве событий.
То есть событиями мы будем называть не любые подмножества Ω, а лишь подмножества из некоторого «множества подмножеств» Ψ. При этом необходимо позаботиться, чтобы это множество Ψ подмножеств Ω было «замкнуто» относительно введенных в параграфе 1.2 операций над событиями, то есть чтобы объединение, пересечение, дополнение событий (то есть элементов Ψ) снова давало событие (то есть элемент Ψ ).
Определение 10. Множество Ψ, состоящее из подмножеств множества Ω, (не обязательно всех!) называется σ - алгеброй событий, или σ – алгеброй подмножеств Ω, если выполнены следующие условия:
(A1) Ω Î Ψ (σ -алгебра событий содержит достоверное событие);
(A2) если ![]() , то
, то ![]() (вместе с любым событием σ -алгебра содержит противоположное событие);
(вместе с любым событием σ -алгебра содержит противоположное событие);
(A3) если А1, А2… Î Ψ, то
![]()
(вместе с любым конечным или счетным набором событий σ -алгебра содержит их объединение).
Условия (A1)–(A3) часто называют «аксиомами σ - алгебры».
Проверим, что этого набора аксиом достаточно для замкнутости множества Ψ относительно других операций над событиями.
Вместо первой аксиомы достаточно предположить, что Ψ не пусто, т.е. содержит хоть один элемент.
Свойство 1. Æ Î Ψ (σ -алгебра событий содержит невозможное событие).
Доказательство. По (A1), Ω Î Ψ, но Æ = Ω/ Ω = ¬ Ω Î Ψ в силу (A2).
Свойство 2. При выполнении (A1),(A2) свойство (A3) эквивалентно свойству (A4)
(A4) если А1, А2… Î Ψ, то
![]()
(вместе с любым конечным или счетным набором событий σ -алгебра содержит их пересечение).
Доказательство. Докажем, что при выполнении (A1),(A2) из (A3) следует (A4).
Если А1, А2… Î Ψ, то при всех i = 1, 2,… по свойству (A2) выполнено ![]()
Тогда из (A3) следует, что
![]()
и, по (A2), дополнение к этому множеству также принадлежит Ψ, то есть
![]()
Но, в силу формул двойственности,
![]()
Доказательство в обратную сторону выглядит совершенно аналогично.
Свойство 3. Если А, ВÎ Ψ , то А\ ВÎ Ψ
Пример 12. Пусть Ω = {1, 2, 3, 4, 5, 6}— пространство элементарных исходов (например, при бросании игрального кубика). Следующие наборы подмножеств Ω являются σ -алгебрами (доказать!):
1. Ψ = { Ω , Æ} ={ {1, 2, 3, 4, 5, 6},Æ }— тривиальная σ -алгебра.
2. Ψ = { Ω , Æ,{1},¬{1}} ={ {1, 2, 3, 4, 5, 6},Æ,{1},{2, 3, 4, 5, 6} }.
3. Ψ = { Ω , A,¬A} ={ {1, 2, 3, 4, 5, 6},Æ, A,¬A }., где A — произвольное подмножество Ω (в предыдущем примере A ={1} ).
Итак, мы определили специальный класс Ψ подмножеств пространства элементарных исходов Ω, названный σ -алгеброй событий, причем применение счетного числа любых операций (таких, как объединение, пересечение, дополнение) к множествам из Ψ снова дает множество из Ψ (не выводит за рамки этого класса). Множества АÎ Ψ мы и назвали «событиями».
Определим теперь понятие «вероятности» как функции, определенной на множестве событий (то есть функции, которая каждому событию ставит в соответствие число). А чтобы читателю сразу стало понятно, о чем пойдет речь, добавим: вероятность мы определим как неотрицательную нормированную меру, заданную на σ -алгебре Ψ подмножеств Ω.
3.2 Вероятность как нормированная мераОпределение 11.
Пусть Ω — некоторое множество и Ψ — σ -алгебра его подмножеств. Функция μ: Ψ → R U {∞} называется мерой на (Ω, Ψ), если она удовлетворяет условиям:
(M1) Для любого множества А Î Ψ его мера неотрицательна: μ(А)≥ 0.
(M2) Для любого счетного набора попарно непересекающихся множеств А1, А2… Î Ψ мера их объединения равна сумме их мер:
(«счетная аддитивность» или «σ -аддитивность»). Иначе говоря, мера есть неотрицательная, счетно-аддитивная функция множеств.
Определение 12.
Пусть Ω — некоторое множество и Ψ — σ -алгебра его подмножеств. Мера μ: Ψ → R называется нормированной, если μ(Ω) = 1. Другое название нормированной меры — «вероятность» или «вероятностная мера».
То же самое еще раз и подробно:
Определение 13.
Пусть Ω — пространство элементарных исходов и Ψ — σ -алгебра его подмножеств (событий). Вероятностью или вероятностной мерой на (Ω, Ψ), называется функция P Ψ → R, обладающая свойствами:
(P1) Для любого события А Î Ψ выполняется неравенство P(А)≥ 0;
(P2) Для любого счетного набора попарно несовместных событий А1, А2… Î Ψ имеет место равенство
![]()
(P3) Вероятность достоверного события равна единице: P(Ω) = 1.
Свойства (P1)–(P3) часто называют «аксиомами вероятности».
Определение 14.
Тройка (Ω, Ψ,Р), в которой Ω — пространство элементарных исходов, Ψ — σ -алгебра его подмножеств и P — вероятностная мера на Ψ, называется вероятностным пространством.
Выпишем свойства вероятности:
0. ![]()
1. Для любого конечного набора попарно несовместимых событий А1, А2… Î Ψ имеет место равенство
![]()
2. ![]()
3. Если ![]() , то
, то ![]()
4. Если ![]() , то
, то ![]()
5. ![]()
6. ![]()
7. ![]()
8. ![]()
9. ![]() (2)
(2)
Пример 13. Кубик подбрасывается один раз. Известно, что выпало более трех очков. Какова при этом вероятность того, что выпало четное число очков?
В данном случае пространство элементарных исходов состоит из трех равновозможных элементарных исходов: Ω = {4, 5, 6}, и событию A = {выпало четное число очков} благоприятствуют 2 из них: A = {4, 6}. Поэтому P(A) = 2/3.
Посмотрим на этот вопрос с точки зрения первоначального эксперимента. Пространство элементарных исходов при одном подбрасывании кубика состоит из шести точек: Ω = {1, 2, 3, 4, 5, 6} . Слова «известно, что выпало более трех очков» означают, что в эксперименте произошло событие B = {4, 5, 6},. Слова «какова при этом вероятность того, что выпало четное число очков?» означают, что нас интересует, в какой доле случаев при осуществлении B происходит и А. Вероятность события А, вычисленную в предположении, что нечто о результате эксперимента уже известно (событие B произошло), мы будем обозначать через P(A/B)
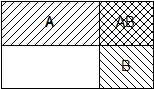 |
Мы хотим вычислить отношение числа исходов, благоприятствующих А внутри B (то есть благоприятствующих одновременно A и B), к числу исходов, благоприятствующих B.
Определение 15. Условной вероятностью события А, при условии, что произошло событие В, называется число
Будем считать, что условная вероятность определена только в случае, когда P(В) > 0.
Следующее свойство называется "теоремой умножения":
Теорема 6. P(A∩B) = P(B)P(A\B) = P(A)P(B\A), если соответствующие условные вероятности определены (то есть если P(В) > 0, P(A) > 0).
Теорема умножения для большего числа событий:
Теорема 7. P(A1 ∩ A2 ∩…∩ An) = P(A1) P(A2\A1) P(A3 \A1 ∩A2)… P(An \A1∩…∩An-1)если соответствующие условные вероятности определены.
4.2 НезависимостьОпределение 16. События A и B называются независимыми, если P(A∩B) = P(A)P(B)
Пример 14.
1. Точка с координатами ξ, η бросается наудачу в квадрат со стороной 1. Доказать, что для любых х, у ÎR события A = { ξ <x} и B= { η <y} независимы.
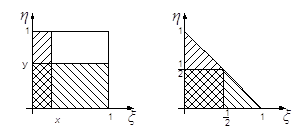 |
2. Точка с координатами ξ, η бросается наудачу в треугольник с вершинами (1,0), (0,0) и (0,1). Доказать, что события A = { ξ <1/2} и B= { η <1/2} зависимы.
Похожие работы
... мышц и скоростью их сокращения, между спортивным достижением в одном и другом виде спорта и так далее. Теперь можно составить содержание элективного курса «Основы теории вероятностей и математической статистики» для классов оборонно-спортивного профиля. 1. Комбинаторика. Основные формулы комбинаторики: о перемножении шансов, о выборе с учетом порядка, перестановки с повторениями, размещения с ...
... случайная величина приобрела статус полноценного математического понятия, ей необходимо дать строго формализованное определение. Это было сделано в конце 20-х годов А.Н. Колмогоровым в небольшой статье, посвященной аксиоматике теории вероятностей, а затем в подробностях изложено в его знаменитой книге «Основные понятия теории вероятностей». Подход Колмогорова стал теперь общепринятым, поскольку он ...
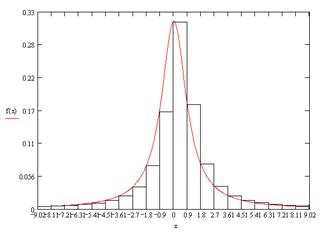
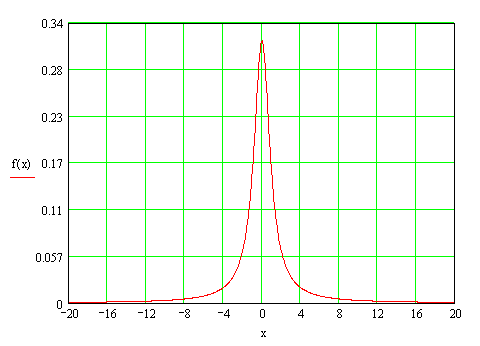
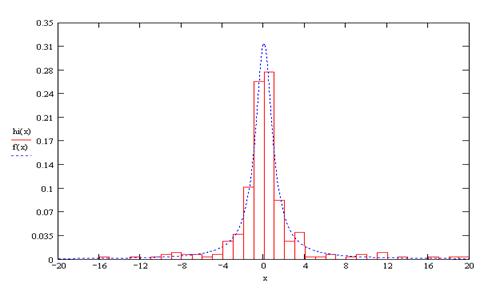
... 400 интервалов). Решение: Построим график плотности распределения по закону Коши (): Рис.2. График распределения Коши. Необходимо разбить интервал от –20 до 20 на n подинтервалов (в данном случае n=40) и вычислить вероятность попадания на каждый из этих подинтервалов. После этого составить массив [a1,aj], так чтобы a1=0, a , случайно сгенерировать значение числа «b» из промежутка от 0 ...
... , причём i – заводпоставляет mi% изделий (i = 1, 2, 3). Среди изделий i – го завода n1% первосортных. Куплено одно изделие. Оно оказалось первосортным. Определить вероятность того, что купленное изделие выпущено i – заводом. m1 = 60 m2 = 20 m3 = 20 n1 = 70 n2 = 80 n3 = 90 Пусть: H1 – поставил первый завод H2 – поставил второй завод H3 – поставил третий завод Пусть: ...



0 комментариев