Навигация
Координаты и компоненты в-ра
17. Координаты и компоненты в-ра
Обозначаем в прямоугольной декартовой системе координат положительные направления осей OX,OY,OZ единичными в-рами : i, j, k, попарно ортогональными и равными единице.
Найдутся числа x,y,z, для которых:
а = xi+yj+zk (2) Эта ф-ла наз. разложением в-ра по орто-базису
Эти в-ры называются ортонормированным базисом. Для каждого в-ра а разложение по орто-базису единственно, т. е. коэффициенты x,y,z в разложении в-ра а по векторам i,j,k определены однозначно. Эти коэффициенты наз координатами в-ра а, они совпадают с координатами z,y,x т. А
a={x,y,z} это означает, что в-р однозначно задается упорядоченной тройкой своих коэффициентов
В-ры xi, yj, zk, сумма которых = а, называются компонентами в-ры а. Два в-ра а и в равны тогда и только тогда, когда равны все их компоненты.
Радиус-вектором в т. М(x,y,z) называется вектор r=xi+yj+zk, идущий из начала коорд т. О в т. М
Линейные операции над в-рами в координатах.
Имеем 2 в-ра а={x1,y1,z1} b={x2,y2,z2}, таких, что а=x1i+y1j+z1k, b=x2i+y2j+xz2k
сумма будет:
a+b=(x1+x2)I+(y1+y2)j+(z1+z2)k
a+b={x1+x2, y1+y2, z1+z2}
при сложении в-ров их координаты попарно складываются. Для вычитания так же.
С×а={Cx1,Cy1,Cz1}
при умножении на число, все его координаты умножаются на это число.
В-ры а и в коллинеарны тогла и только тогда, когда их координаты пропорциональны.
18. Проекция в-ра на ось
Прямая l, с заданным на ней направлением называется осью.
Величиной направленного отрезка Ав на оси l наз. число, обозначаемое: (АВ) и равное длине отрезка АВ, взятом со знаком +, если напр АВ совп с напр. прямой и со знаком – если не совп.
Проекцией в-ра АВ на ось l наз величина, направленного отрезка СД, построенного опусканием перпендикуляров из в-ра АВ на ось l, обозн: PrlAB=(СД)
Свойства проекции:
1 Проекция в-ра АВ на какую-либо ось l = произведению длины в-ра на косинус угла между осью и этим в-ром.
PrlAB=|AB|×cosa
2 Проекция на ось l в-ра С×а =С× Prlа, С- произв. число.
3 Проекция суммы в-ров на какую либо ось = сумме проекции в-ров на эту же ось
19. Скалярное пр-е в-ра
20. Векторное пр-е в-ра
21. Смешанное пр-е в-ров
22. Деление отрезка в данном отношении
т М ¹ В делит отрезок [АВ] в отношении l, если АМ = l× АВ. Т. М расположена на Ав при этом, если
1 М внутренняя точка АВ, то l >0 (случайц внутреннего деления)
2 М=А, l = 0
3 М лежит вне Ав, l <0 (случай внешнего деления)
Других вариантов расположения т. М быть не может, и ни водном из вариантов l ¹ -1
Если А(r1), B(r2), M(r) – точки пространства и М – делит АВ в отн l, тогда:
![]() это соотношение в координатной форме имеет вид: для А(x1,y1,z1), B(x2,y2,z2) и M(x,y,z)
это соотношение в координатной форме имеет вид: для А(x1,y1,z1), B(x2,y2,z2) и M(x,y,z)
![]()
![]()
![]()
![]() Если М – середина АВ, то l =1Коорд x,y,z середины отрезка АВ выглядят так:
Если М – середина АВ, то l =1Коорд x,y,z середины отрезка АВ выглядят так:
![]()
![]()
Если т А В принадлежат плоскости ОХУ, то аппликата т А и В и М = 0 и задачу решают первые 2 ф-лы ,а если А и В М лежат на плоскости ОХ, тор первой ф-лой.
23. Нормальное уравнение прямой. Общее уравнение прямой
Если взять на плоскости фиксированную точку О и какую-либо прямую L, то положение этой прямой относительно плоскости будет определено если задать расстояние от нее до т. О, т. е. длину р отрезка ОТ, перпендикуляра из т. О на эту прямую; и единичный вектор n0=1 – перпендикулярный прямой L и направленный из начальной т. О к этой прямой.
Когда текущая т. М движется по прямой L, радиус вектор-r меняется так, что проекция на направление n0 будет постоянной и равной р:
![]() это соотношение выполняется для каждой точки прямой L и нарушается когда т. М лежит вне ее.
это соотношение выполняется для каждой точки прямой L и нарушается когда т. М лежит вне ее.
Заметив, что:![]() это можно записать так:
это можно записать так:
![]() (2) полученное ур-е наз. нормальным (нормированным) уравнением прямой в векторной форме. Радиус в-р r – произвольной точки прямой наз. текущим радиус в-ром прямой.
(2) полученное ур-е наз. нормальным (нормированным) уравнением прямой в векторной форме. Радиус в-р r – произвольной точки прямой наз. текущим радиус в-ром прямой.
Выбрав на плоскости Декартову систему координат и поместив ее начало в т. О, в-ры r, n0 можно записать так:
n0={cosj, sinj}; r={x,y}
уравнение (2) примет вид:
![]() (3) это нормальное уравнение прямой в координатной форме, относительно прямых х и у; оно явл ур-ем 1 степени, тем самым в Декартовой прямоугольной системе всякое положение прямой определяется ур-ем 1 степени относительно переменных х и у верно и обратное.
(3) это нормальное уравнение прямой в координатной форме, относительно прямых х и у; оно явл ур-ем 1 степени, тем самым в Декартовой прямоугольной системе всякое положение прямой определяется ур-ем 1 степени относительно переменных х и у верно и обратное.
Уравнение Ax+By+C=0 (4) называется общим уравнением прямой А2+В2 ¹ 0
если домножить его на постоянный множитель m, положа:
m×А= cosj, m×В= sinj, m×С = -р, где:
![]()
называется нормирующим множителем.
И уравнение получается нормальным .Общее уравнение (4) определяет прямую как множество точек М плоскости декартовы координаты которых удовлетворяют этому уравнению.
![]() Нормальный в-р прямой - всякий ненулевой (не обязательно- единичный) в-р перпендикулярный этой прямой. Вектор n = {A,B} будет нормальным вектором прямой, заданной ур-ем (4), таким оборазом коэффициенты А и В при текущих координатах х и у являются координатами нормального в-ра этой прямой. Все отсальный нормальные в-ры прямой можно получить умножая в-р n на произвольное ¹ 0 число.
Нормальный в-р прямой - всякий ненулевой (не обязательно- единичный) в-р перпендикулярный этой прямой. Вектор n = {A,B} будет нормальным вектором прямой, заданной ур-ем (4), таким оборазом коэффициенты А и В при текущих координатах х и у являются координатами нормального в-ра этой прямой. Все отсальный нормальные в-ры прямой можно получить умножая в-р n на произвольное ¹ 0 число.
24. Уравнение прямой на плоскости , проходящей через заданную точку перпендикулярно заданному направлению.
Для того, чтобы найти ур-е прЯмой L, проходящей через т. М0, заданную радиус-вектором r0={x0,y0}, перпендикулярную вектору n={A,B}, проведем радиус-вектор r={x,y} в произвольной т. М этой прямой
в-р М0М = r-r0 лежит на прямой L, а значит перпендикулярен в-ру n, поэтому их скалярное пр-е = 0
(r-r0)× n = 0 (8) равенство справедливо для всех т. М принадлежащих прямой и нарушается, если точка на прямой не лежит. Ур-е (8) явл в-рным уравнением исходной прямой выражая это произв, через коорд в-ров получим ур-е прямой в коорд форме:
A(x-x0)+B(y-y0)=0 (9)
25. Исследование уравнения прямой неполные ур-я прямой..
Если хотя бы один из коэффициентов А, В, С ур-я Ах+Ву+С=0 равен 0, ур-е наз. неполным. По виду уравнения прямой можно судить о ее положении на плоксоти ОХУ. Возможны случаи:
1 С=0 L: Ax+By=0 т. О(0,0) удовлетворяет этому уравнению значит прямая проходит через начало координат
![]() 2 А=0 L: Ву+С=0 - нормальный в-р n={0,B} перпендикулярен оси ОХ отсюда следует, что прямая параллельна ось ОХ
2 А=0 L: Ву+С=0 - нормальный в-р n={0,B} перпендикулярен оси ОХ отсюда следует, что прямая параллельна ось ОХ
![]() 3 В = 0 L: Ay+C=0 0 - номральный в-р n={А,0} перпендикулярен оси ОY отсюда следует, что прямая параллельна ось ОУ
3 В = 0 L: Ay+C=0 0 - номральный в-р n={А,0} перпендикулярен оси ОY отсюда следует, что прямая параллельна ось ОУ
4 А=0, С=0 L: By=0Ûy=0ÛL=OX
5 B=0, C=0 L: Ax=0Ûx=0ÛL=OY
6 A ¹ 0, В ¹ 0, С ¹ 0 L; - не проходит через начало координат и пересекает обе оси.
26. Уравнение прямой с угловым коэффициентом
Если общее уравнение прямой, при В ¹ 0 переписать в виде:
![]() и приравняв:
и приравняв:
![]() и
и ![]() получим ур-е с угловым коэффициентом
получим ур-е с угловым коэффициентом
у=кх+b (10), где число к = tga, a - величина угла наклона прямой к оси ОХ, угол, отсчитываемый в направлении противоположном движению часовой стрелки от положительного направления оси ОХ до данной прямой.
В случае L||ОХ, или L=OX, a=0
В случае L||ОY, или L=OY, a=П/2 и угловой коэффициент не существует.
Похожие работы
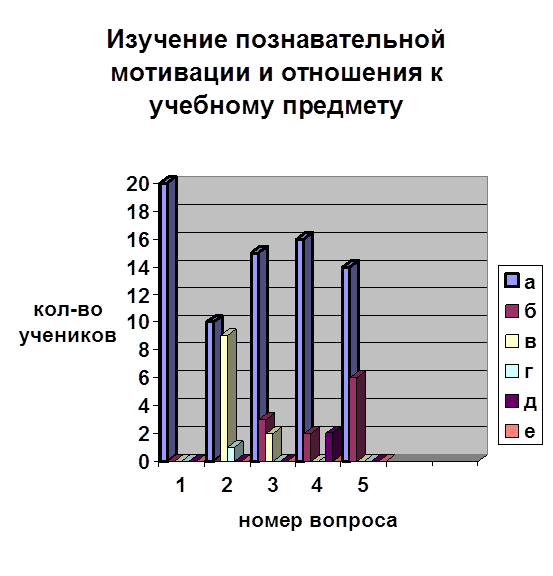
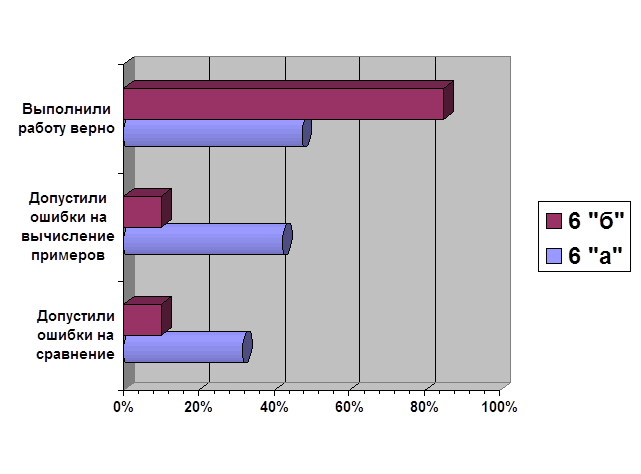
... дидактических игр на уроках математики, анализ игровой деятельности Изучив теоретические материалы по развитию мотивации познавательной деятельности, у автора возникло желание и интерес реализации этого на практике. Для того чтобы доказать или опровергнуть, что использование дидактических игр на уроках математики активизирует познавательную деятельность учащихся, автором работы в 6 «б» ...



0 комментариев