Навигация
Ур-е прямой, проход через данную т., с данным угловым коэфф. Ур-е прямой проход через две данные точки
27. Ур-е прямой, проход через данную т., с данным угловым коэфф. Ур-е прямой проход через две данные точки.
Если прямая задана т М0(х0, у0) и угловым коэффициентом к, тогда на основании ур-я (10) можно получить ур-е искомой прямой:
у-у0=к(х-х0) (11)
Ур-е прямой проходящей через две заданных точки
Зададим прямую точками М1(х1,у1) и М2(х2,у2), х1 ¹ х2. М1 и М2 принадлежат прямой, откуда следует:
у-у1=к(х-х1) для М1и у-у2=к(х-х2) для М2
откуда:
(12) Эта ф-ла позволяет вычисли ть угловой коэффициент, зная коорд двух точек.
Если у1 ¹ у2, то подставляя к из ф-лы (12) в равенство: у-у1=к(х-х1), получаем:
![]() (13) Искомое уравнении прямой, проход через две заданных точки.
(13) Искомое уравнении прямой, проход через две заданных точки.
28. Расстояние от точки до прямой на плоскости
Расстоянием от т. М* до прямой L наз. длину отрезка М*N – перпендикуляра L^ опущенного из т. М* на эту прямую.
Если М*(х*, у*) – заданная точка,
а ![]() - нормальное ур-к прямой L, то расстояние от М* до L выч. по ф-ле:
- нормальное ур-к прямой L, то расстояние от М* до L выч. по ф-ле:
d=d(M*,L)=|x*cosj+y*sinj-p| (14)
d=d(M*,L)=|rx×n0 -p|
обозначим через d(M*,L)= rx×n0 –p= x*cosj+y*sinj-p т. е.: d(M*,L)= |d|
по знаку d можно судить о расположении точек О и М*, относительно прямой L:
Если О и М* расположены по разные стороны относительно прямой, то d > 0 , если по одну сторону – то d<0. Величина d называется отклонением т. М* от прямой L.
Если прямая задана общим уравнением, то расстояние вычисляется по ф-ле:
![]()
29. Уравнение прямой в отрезках
Рассматривая общее ур-е прямой, при А,В,С ¹ 0, переписав его в виде:
![]() и положив
и положив
а = - С/A в = - С/В получим ур-е прямой в отрезках:
![]() (16)
(16)
Для нахождения т. М1 пересечения прямой (16) с осью ОХ достаточно решить систему уравнений:
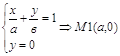
для пересечения с осью ОУ получаем:
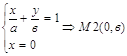
Параметры а и в в(16) определяют величину отрезков Ом1 и ОМ2, отсекаемых прямой от осей координат.
30. каноническое уравнение прямой
Ненулевой в-р коллинеарный прямой называется ее направляющим в-ром.
Из аксиом следует, что через заданную точку проходит только одна прямая с заданным направляющим в-ром.
Прямая L, с направл. в-ром S проходящая через т. М0(х0, у0). проходит через т. М(х,у) тогда и только тогда, когда в-ры М0М и S 0 коллинеарны т. е. М0М=tS, t'R) (17) Это ур-е наз векторным уравнением прямой.
Если М0(х0, у0), М(х,у) – текущие точки прямой L; S={m,n} – направляющий вектор прямой , тогда в-р М0М = {x-x0, y-y0}
Записав условия коллинеарности из (17) в векторной форме получим: x-x0=tm, y-y0=tn или:
![]() (18) Ур-е наз. каноническим ур-ем прямой на плоскости.
(18) Ур-е наз. каноническим ур-ем прямой на плоскости.
![]() Обозначает лишь пропорциональность и в случае, когда m = 0 или n = 0 равносильно ур-ям: х-х0=0 или у-у0=0 соответственно.
Обозначает лишь пропорциональность и в случае, когда m = 0 или n = 0 равносильно ур-ям: х-х0=0 или у-у0=0 соответственно.
31. ![]() Параметрическое уравнение прямой на плоскости.
Параметрическое уравнение прямой на плоскости.
Представляет собой другую форму записи ур-я (17)
пусть r=ОМ, а r0=OM0 – радиус в-ры точек М и М0 относительно начала координат, тогда М0М = r-r0 и ур-е (17) зап. в виде: r=r0+tS, t'R
или в координатной форме, в системе ОХУ:
![]() (20), t'R
(20), t'R
ур-я (19) и (20) наз параметрическими уравнениями прямой на плоскости в векторной и координатной формах.
32. Угол между двумя прямыми на плоскости.
Условия параллельности и перпендикулярности двух прямых на плоскости
а) прямые L1 L2 заданы общими уравнениями
L1:=А1х+В1у+С1=0, А12+В12>0
L2:=А2х+В2у+С2=0, А22+В22>0
j(угол между ними)= углу между их нормальными в-рами n1 ={A1,B1} и n2={A2,B2}
оттуда вытекает, что
![]()
L1|| L2 Û n1 || n2Û n1 = ln2
A1=lA2, B1=lB2
![]()
L1 ^ L2 Û n1 ^ n2Û n1×n2 =0 Û
Û A1×A2+B1×B2=0
б) прямые заданы каноническим уравнением
угол между ними равен углу между их направляющими векторами:
S1={m1,n1} S2{m2,n2} поэтому:
![]() L1|| L2 Û S1 || S2
L1|| L2 Û S1 || S2
![]()
L1 ^ L2 Û S1 ^ S2 Û S1×S2=0 Û
m1×m2+n1×n2=0
в) прямые заданы ур-ем с угловым коэффициентом
L1:= у=к1х+в1
L2:= у=к2х+в2
за угол между прямыми принимаемся наименьший угол на который нужно повернуть прямую L1 против часовой стрелки до совмещения с прямой L2 вокруг т. пересечения прямых.
Через a1 и a2 обоз углы наклона прямых L1 и L2 к оси ОХ
Угол между прямыми j= a2- a1
![]()
tga1=k1, tga2=k2
![]()
L1|| L2 Û a1 = a2 (j=0) Û k1=k2
L1 ^ L2 Û j=П/2
k2= -1/k1
Похожие работы
... дидактических игр на уроках математики, анализ игровой деятельности Изучив теоретические материалы по развитию мотивации познавательной деятельности, у автора возникло желание и интерес реализации этого на практике. Для того чтобы доказать или опровергнуть, что использование дидактических игр на уроках математики активизирует познавательную деятельность учащихся, автором работы в 6 «б» ...
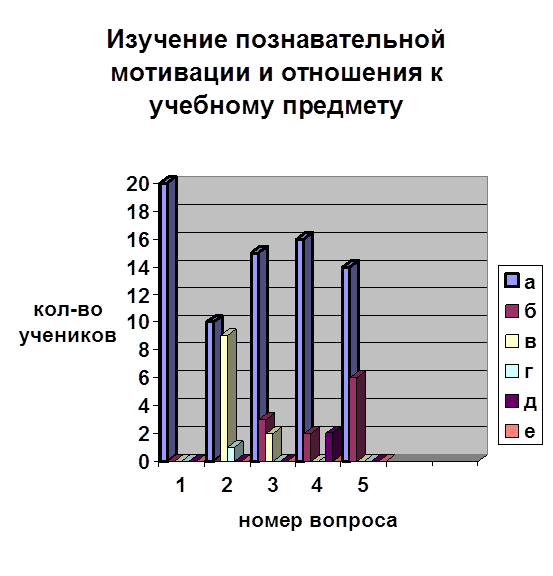



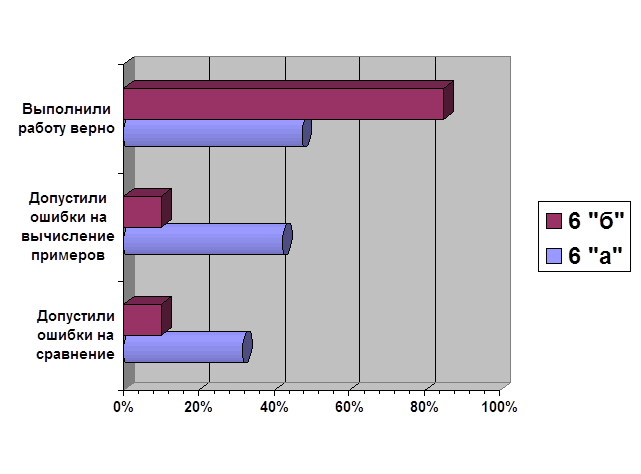
0 комментариев