Навигация
1. Имеем
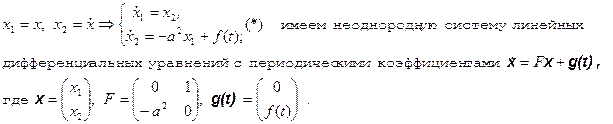
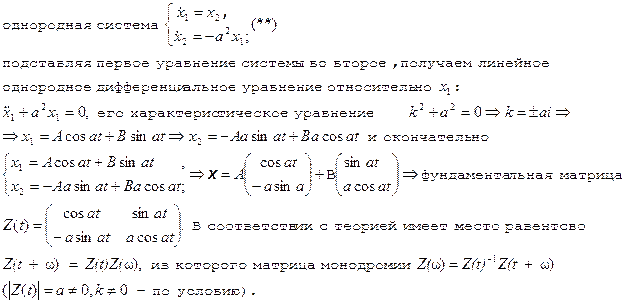
2. Для применения теоремы 2 нам необходимо составить матрицу монодромии однородной системы и все собственные значения этой матрицы должны быть отличны от единицы; для начала найдем фундаментальную матрицу для однородной системы, соответствующей неоднородной системе (*):
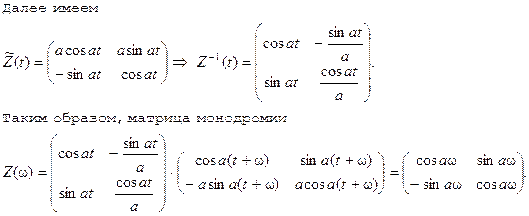
3. Находим мультипликаторы однородной системы:
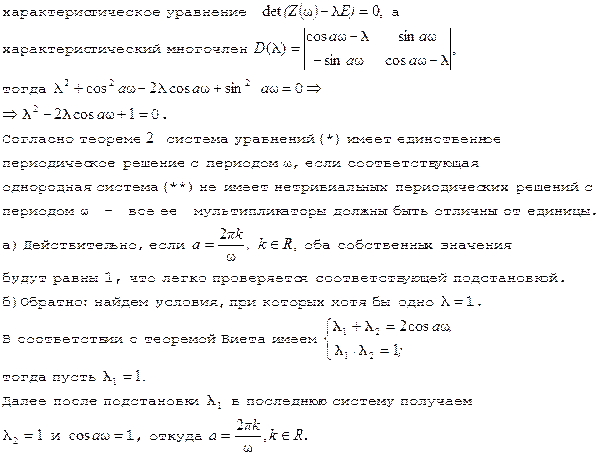
![]() Итак, если
Итак, если
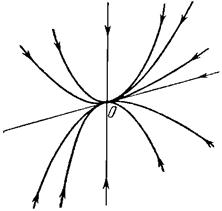
все мультипликаторы системы уравнений (**) отличны от единицы.Таким образом, выполнены все условия теоремы 2. Из этого следует, что система (*),а значит и исходное дифференциальное уравнение, имеет единственное периодическое решение с периодом ω.
Задача решена.
Пример 2: Показать, что линейное уравнение второго порядка
![]()
при a≠2πk/ω (kÎR) имеет единственное периодическое решение с периодом ω (см. пример 1); при a=±2π/ω не имеет периодических решений с периодом ω, а при a=2πk/ω (k — любое целое число, не равное ±1 и 0) все его решения — периодические с периодом ω.
Решение.
Очевидно, что здесь необходимо воспользоваться теоремой 2 и замечанием к ней. Решение данного примера необходимо разбить на 3 части (для каждого из условий). Поскольку при нахождении матрицы монодромии в предыдущем примере мы свободный член исходного дифференциального уравнения не использовали и учитывая одинаковые правые части дифференциальных уравнений обоих примеров, можно будет сразу воспользоваться некоторыми выкладками примера 1.
Итак, матрица монодромии имеет следующий вид:
![]() 1.[a≠2πk/ω (kÎR)] Как мы установили в примере 1, любое линейное уравнение вида при указанных ограничениях действительно имеет единственное периодическое решение с периодом ω.
1.[a≠2πk/ω (kÎR)] Как мы установили в примере 1, любое линейное уравнение вида при указанных ограничениях действительно имеет единственное периодическое решение с периодом ω.
2-3.[a=±2π/ω; a=2πk/ω (k — любое целое число, не равное ±1 и 0)]
При данных значениях а однородная система (**) из 1-го примера имеет нетривиальное периодическое решение с периодом ω, тогда в соответствии с замечанием к теореме 2 линейная неоднородная система уравнений, соответствующая заданному дифференциальному уравнению , может или вообще не иметь периодических решений с периодом ω (для случая 2 необходимо установить несовместность системы уравнений (13)), или иметь несколько периодических решений с периодом ω (для случая 3 необходимо установить, что система уравнений (13) имеет бесконечное множество решений).
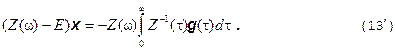 Сначала мы будем случаи 2 и 3 рассматривать совместно:
Сначала мы будем случаи 2 и 3 рассматривать совместно:
Система уравнений (13):
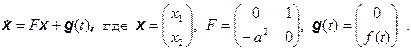 Неоднородная система, соответствующая заданному дифференциальному уравнению:
Неоднородная система, соответствующая заданному дифференциальному уравнению:

Далее решать систему будем отдельно для каждого заданного значения а:
если в системе (***) справа будет получена нулевая матрица, то она имеет множество решений, если нет – не имеет их вообще.
2. Подставляем в систему (***)a=±2π/ω:
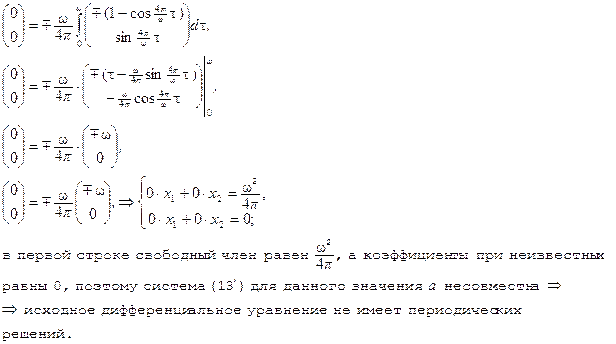
![]()
3. Подставляем в систему (***)a=2πk/ω (k — любое целое число, не равное ±1 и 0):
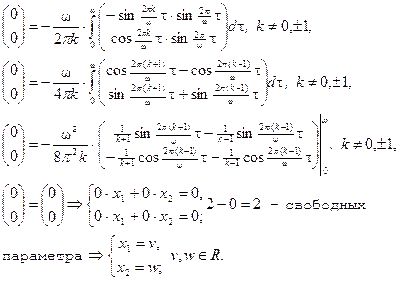
Таким образом,система (13') имеет бесконечное множество решений для данных значений а Þ исходное дифференциальное уравнение имеет несколько линейно независимых периодических решений с периодом ω.
Замечание. Отдельно стоит рассмотреть случай, когда а=0 (этому случаю соответствует k=0, если a=2πk/ω).
Если а=0, то матрицы, обратной фундаментальной матрице системы (**), не существует, отсюда сразу следует несовместность системы (13'), а значит исходное линейное уравнение второго порядка не имеет периодических решений.
Задача решена.
[1]
Похожие работы
... начальным условиям . Пусть — характеристическое уравнение для определения мультипликаторов. Так как , то оно принимает вид , где . 2. Устойчивость решений систем дифференциальных уравнений. 2.1. Устойчивость по Ляпунову. Вводя определение устойчивости по Лагранжу и Пуассону в пункте 1.3, описывались свойства одной отдельно взятой траектории. Понятие устойчивости по Ляпунову характеризует ...
... шаг интегрирования ; tp – время интегрирования трех точечным методом прогноза и коррекции , ta – время интегрирования по методу Адамса-Башфорта , NU – массив начальных условий . Данная процедура способна производить решения систем линейных дифференциальных уравнений произвольного размера , на произвольном промежутке времени интегрирования . Вычисленные данные записываются в файлы prandcom*.df . ...
... была построена теория вложения функциональных пространств, которые в настоящее время носят название пространств Соболева. А.Н. Тихоновым была построена теория некорректных задач. Выдающийся вклад в современную теорию дифференциальных уравнений внесли российские математики Н.Н. Боголюбов, А.Н. Колмогоров, И.Г. Петровский, Л.С. Понтрягин, С.Л. Соболев, А.Н. Тихонов и другие. Влияние на развитие ...
... , является важнейшей вспомогательной научно-технической задачей . Целью данной курсовой работы является разработка алгоритма решения систем линейных дифференциальных уравнений первого порядка пяти точечным методом прогноза и коррекции Адамса-Башфорта . 1. ПОСТАНОВКА ЗАДАЧИ Рассмотрим произвольную систему линейных дифференциальных уравнений первого порядка : ...
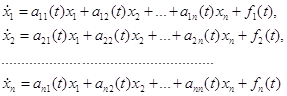
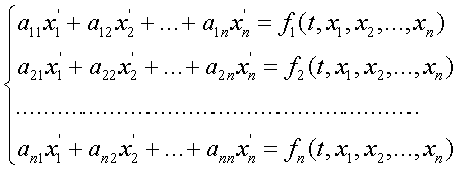
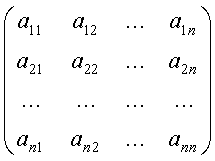
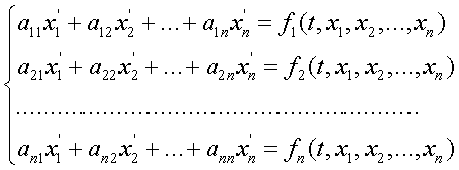
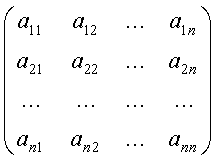
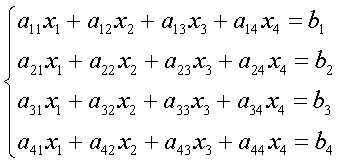
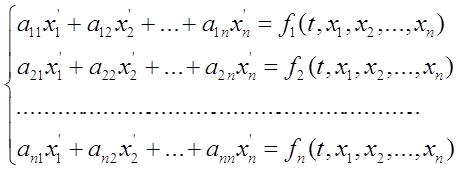

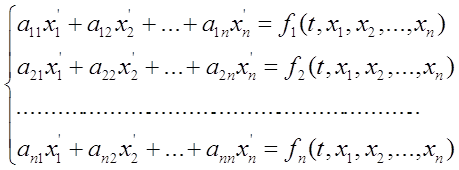
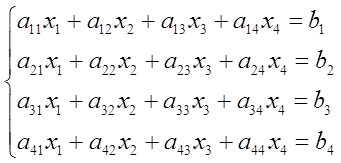
0 комментариев