Навигация
Численное дифференцирование и интегрирование
4. Численное дифференцирование и интегрирование
Если функция f(x) заданна аналитически ее первообразная F(x) является элементарной функцией, то 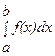 вычисляется по формуле Ньютона-Лейбница:
вычисляется по формуле Ньютона-Лейбница:  В тех случаях, когда функция f(x) задана аналитически, но ее первообразная не является элементарной функцией или отыскать ее сложно, а также в случае, когда функция f(x) задана графически или таблично, для вычисления
В тех случаях, когда функция f(x) задана аналитически, но ее первообразная не является элементарной функцией или отыскать ее сложно, а также в случае, когда функция f(x) задана графически или таблично, для вычисления 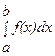 применяются приближенные методы.
применяются приближенные методы.
Постановка задачи численного интегрирования
Задача численного интегрирования функции заключается в вычислении определенного интеграла на основании ряда значений подынтегральной функции. Численное вычисление однократного интеграла называется механической квадратурой. Обычный прием механической квадратуры состоит в том, что данную функцию f(x) на рассматриваемом отрезке [a, b] заменяют интерполирующей или аппроксимирующей функцией φ(x) простого вида, а затем приближенно полагают: 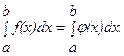 Функция φ(x) должна быть такова, чтобы интеграл
Функция φ(x) должна быть такова, чтобы интеграл 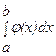 вычислялся непосредственно. Если функция f(x) заданна аналитически, то ставится вопрос об оценке погрешности. Пусть для функции y=f(x) известны в n+1 точках x0, x1, x2, …, xn отрезка [a, b] соответствующие значения f(xi)=yi
(i=0, 1, 2, …, n). Требуется приближенно найти
вычислялся непосредственно. Если функция f(x) заданна аналитически, то ставится вопрос об оценке погрешности. Пусть для функции y=f(x) известны в n+1 точках x0, x1, x2, …, xn отрезка [a, b] соответствующие значения f(xi)=yi
(i=0, 1, 2, …, n). Требуется приближенно найти 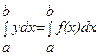 По заданным значениям yi построим полином Лагранжа
По заданным значениям yi построим полином Лагранжа 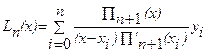 , где
, где
Пn+1(x)=(x-x0)(x-x1)…(x-xn), причем Ln(xi)=yi
(i=0, 1, 2, …, n). Заменяя функцию f(x) полиномом Ln(x), получим равенство 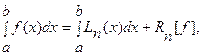 где Rn[f] – ошибка квадратурной формулы. Отсюда получаем приближенную квадратурную формулу
где Rn[f] – ошибка квадратурной формулы. Отсюда получаем приближенную квадратурную формулу
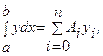 где
где 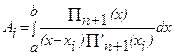 (i=0, 1, 2, …, n). Для вычисления Ai заметим, что
(i=0, 1, 2, …, n). Для вычисления Ai заметим, что
1) коэффициенты Ai при данном расположении узлов не зависят от выбора функции f(x);
2) для полинома степени n полученная формула – точная, так как тогда Ln(x)=f(x); следовательно, формула 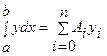 - точная при y=xk (k=0, 1, 2, …, n), т.е. Rn[xk]=0 при k=0, 1, …, n. Полагая y=xk
(k=0, 1, 2, …, n), получим линейную систему из n+1 уравнений
- точная при y=xk (k=0, 1, 2, …, n), т.е. Rn[xk]=0 при k=0, 1, …, n. Полагая y=xk
(k=0, 1, 2, …, n), получим линейную систему из n+1 уравнений 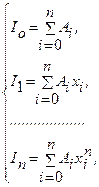 - где
- где 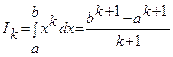 (k=0, 1, …, n), из которой можно определить коэффициенты A0, A1, …, An.
(k=0, 1, …, n), из которой можно определить коэффициенты A0, A1, …, An.
Составные квадратурные формулы
Приведем ряд простейших квадратурных формул, используемых в практике численного интегрирования функции f(x) на некотором интервале [a, b], разбитого на n равных отрезков точками a0=a, a1=a+h, a2=a+2h, …, an=a+nh+b, где n=0,1, …, k и ![]() Положим f(xn)=yn=f(a+nh).
Положим f(xn)=yn=f(a+nh).
Формула прямоугольников: 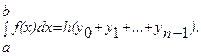
Погрешность формулы определяется выражением
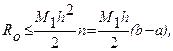 где
где ![]()
Формула трапеций: 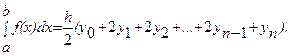
Погрешность формулы определяется выражением
![]() где
где ![]()
Формула Симпсона: 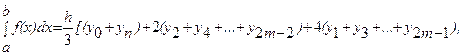 где
где ![]()
Погрешность формулы определяется выражением
![]() где
где ![]()
Если длина интервала [a, b] велика для применения простейших квадратурных формул, то поступают следующим образом:
1) интервал [a, b] разбивают точками xi, ![]() на n интервалов по некоторому правилу;
на n интервалов по некоторому правилу;
2) на каждом частичном интервале [xi, xi+1] применяют простейшую квадратурную формулу, находят приближенное значение интеграла 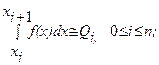
3) из полученных выражений Qi составляют (отсюда и название составная формула) квадратурную формулу для всего интервала [a, b];
4) абсолютную погрешность R составной формулы находят суммированием погрешностей Ri на каждом частичном интервале.
Похожие работы
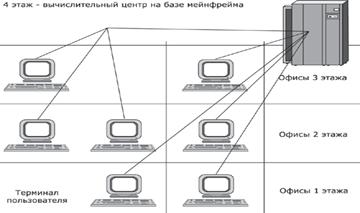
... в какой-то степени являлись прообразом современных компьютерных сетей (рис.1.2), а соответствующее системное программное обеспечение — прообразом сетевых операционных систем. Рис. 1.2 Многотерминальная система — прообраз вычислительной сети Многотерминальные централизованные системы уже имели все внешние признаки локальных вычислительных сетей, однако по существу ими не являлись, так как ...
... ; - показывать, за счет каких структурных особенностей достигается увеличение производительности различных вычислительных систем; с этой точки зрения, классификация может служить моделью для анализа производительности. 1.12 Классификация Дазгупты Одним из последних исследований по классификации архитектур, по-видимому, является работа С. Дазгупты, вышедшая в 1990 году. Автор ...
... ? 8. Какими программами можно воспользоваться для устранения проблем и ошибок, обнаруженных программой Sandra? Раздел 3. Автономная и комплексная проверка функционирования и диагностика СВТ, АПС и АПК Некоторые из достаточно интеллектуальных средств вычислительной техники, такие как принтеры, плоттеры, могут иметь режимы автономного тестировании. Так, автономный тест принтера запускается без ...
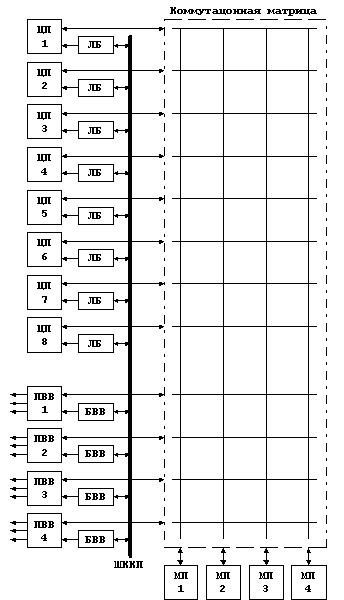
... процесса, а либо вообще не сказываются на работе МПВК, либо вызывают постепенную деградацию вычислительной мощности. Меры по обеспечению отказоустойчивости свои для каждого компонента МПВК. Отказы оперативной памяти были рассмотрены выше. Отказы в коммутационной матрице также как и отказы оперативной памяти целесообразно маскировать применением кодов, корректирующих ошибки. Наиболее сложны для ...
0 комментариев