Навигация
Приближенные методы решения дифференциальных уравнений с частными производными
6. Приближенные методы решения дифференциальных уравнений с частными производными
Кроме обычных дифференциальных уравнений существуют так называемые дифференциальные уравнения с частными производными. Далее они будут рассмотрены более подробно.
Классификация дифференциальных уравнений второго порядка
Рассмотрим уравнение второго порядка 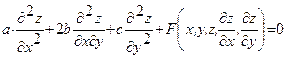 , где
, где ![]() - функции
- функции ![]() и
и ![]() . Говорят, что указанное уравнение в области
. Говорят, что указанное уравнение в области ![]() принадлежит гиперболическому типу, если в этой области
принадлежит гиперболическому типу, если в этой области ![]() . Если
. Если ![]() , то уравнение в области
, то уравнение в области ![]() принадлежит параболическому типу. Если
принадлежит параболическому типу. Если ![]() , то уравнение принадлежит эллиптическому типу.
, то уравнение принадлежит эллиптическому типу.
Уравнение 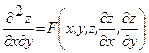 называется каноническим уравнением гиперболического типа.
называется каноническим уравнением гиперболического типа.
Уравнение 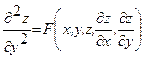 называется каноническим уравнением параболического типа.
называется каноническим уравнением параболического типа.
Уравнение 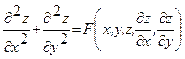 называется каноническим уравнением эллиптического типа.
называется каноническим уравнением эллиптического типа.
Дифференциальное уравнение ![]() называется уравнением характеристик уравнения
называется уравнением характеристик уравнения 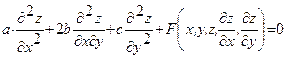 .
.
Если последнее уравнение гиперболического типа, то уравнение характеристик имеет два интеграла: ![]() т.е. существуют два семейства вещественных характеристик.
т.е. существуют два семейства вещественных характеристик.
С помощью замены переменных ![]() ,
, ![]() дифференциальное уравнение
дифференциальное уравнение 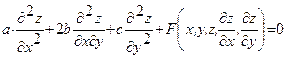 приводится к каноническому виду:
приводится к каноническому виду: 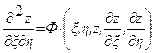 . Для уравнения параболического типа оба семейства характеристик совпадают, т.е. уравнение характеристик дает лишь один интеграл
. Для уравнения параболического типа оба семейства характеристик совпадают, т.е. уравнение характеристик дает лишь один интеграл ![]() .
.
В этом случае осуществляем замену переменных ![]() ,
, ![]() , где
, где ![]() — какая-нибудь функция, для которой
— какая-нибудь функция, для которой ![]() . После замены переменных получаем уравнение
. После замены переменных получаем уравнение 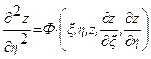 . Для уравнения эллиптического типа интегралы уравнения характеристик имеют вид
. Для уравнения эллиптического типа интегралы уравнения характеристик имеют вид ![]() , где
, где ![]() и
и ![]() — вещественные функции.
— вещественные функции.
Полагая ![]() и
и ![]() , приводим уравнение
, приводим уравнение 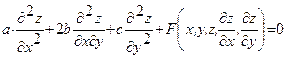 к виду
к виду  .
.
Постановка краевых задач
Классическим решением краевой задачи называются всяка функция, удовлетворяющая дифференциальному уравнению в каждой точке внутри области задания этого уравнения и непрерывная в рассматриваемой области, включая границу. Соответствующую постановку краевой задачи называют классической. Существует несколько таких задач:
Задача Коши для бесконечной области. Рассмотрим эту задачу на примереуравнения колебания струны и уравнения теплопроводности.
Рассмотрим процесс колебания тонкой бесконечной струны под действием непрерывно распределенной внешней силы с плотностью f. Предположим, что сила действует в одной плоскости – плоскости колебания струны (x, u), а струна является гибкой упругой нитью. Пусть величина натяжения, возникающая в струне вследствие ее изгиба, подчиняется закону Гука, а сами колебания достаточно малы. Тогда величина смещения u (x, t) удовлетворяет уравнению колебания струны: ![]() . Для однозначности процесса необходимо задать еще начальное смещение и начальное распределение скоростей. Математически это соответствует заданию начальных условий:
. Для однозначности процесса необходимо задать еще начальное смещение и начальное распределение скоростей. Математически это соответствует заданию начальных условий: ![]() . Требуется найти классическое решение уравнения, удовлетворяющие начальным условиям. Сформулированная таким образом задача называется задачей Коши для гиперболического уравнения.
. Требуется найти классическое решение уравнения, удовлетворяющие начальным условиям. Сформулированная таким образом задача называется задачей Коши для гиперболического уравнения.
Исследуем теперь процесс распределения температуры в тонком бесконечном стержне. Предполагается, что тепловой поток подчиняется закону Фурье, а изменение температуры тела пропорционально количеству теплоты, сообщаемой телу. Предположим, что внутри стержня может выделяться и поглощаться теплота, характеризуемая плотностью тепловых источников f. Тогда распределение температуры в стержне описывается уравнением теплопроводности: ![]() . Для однозначного задания процесса необходимо указать начальное распределение температуры. Это соответствует заданию начального условия:
. Для однозначного задания процесса необходимо указать начальное распределение температуры. Это соответствует заданию начального условия: ![]() . Требуется найти классическое решение уравнения, удовлетворяющие начальным условиям. Сформулированная таким образом задача называется задачей Коши для параболического уравнения.
. Требуется найти классическое решение уравнения, удовлетворяющие начальным условиям. Сформулированная таким образом задача называется задачей Коши для параболического уравнения.
режим распределения температуры в ограниченной тонкой пластине произвольной формы с гладкой границей. Пусть функция u(x, y) выражает температуру каждой точки пластины. При обычных законах распространения тепла функция u(x, y) удовлетворяет уравнению Пуассона: ![]() , где функция а задает плотность тепловых источников пластины. В случае отсутствия источника (f=0) данное уравнение называется уравнением Лапласа:
, где функция а задает плотность тепловых источников пластины. В случае отсутствия источника (f=0) данное уравнение называется уравнением Лапласа: ![]() . Для однозначного описания процесса необходимо задать тепловой режим на границе пластины. Это может быть сделано с помощью задания распределения температуры на границе или распределения теплового потока. Возможен также режим теплового равновесия излучающего тела с окружающей средой.
. Для однозначного описания процесса необходимо задать тепловой режим на границе пластины. Это может быть сделано с помощью задания распределения температуры на границе или распределения теплового потока. Возможен также режим теплового равновесия излучающего тела с окружающей средой.
В зависимости от теплового режима на границе получаются три граничных условия для функции u(x, y). Пусть Г – граница рассматриваемой области D – определения уравнения Лапласа. Математическая формулировка граничных условий может быть задана в следующем виде:
граничное условие I рода: ![]() ;
;
граничное условие II рода: ![]() ;
;
граничное условие III рода: ![]() .
.
Производная берется по внешней нормали к кривой Г; λ>0 – коэффициент теплопроводности; φ0, φ1, φ2 – заданные на Г функции, причем φ2 есть произведение коэффициента теплопроводности на температуру внешней среды, соприкасающейся с телом.
Таким образом, краевая задача заключается в том, чтобы найти классическое решение уравнения Пуассона или Лапласа, удовлетворяющее одному из граничных условий.
Смешанная краевая задача. Рассмотрим задачу распространения тепла в тонкомстержне единичной длины. Поместим один из концов в точку x=0, а другой – в точку x=1. Распределение температуры в таком стержне в течение некоторого интервала времени 0<t<T описывается уравнением ![]() , с начальным условием
, с начальным условием ![]() , а для единственности решения в этом случае необходимо еще задать температурный режим на концах стержня. Это можно сделать с помощью граничных условий, аналогичных тем, которые были сформулированы для уравнений Пуассона и Лапласа.
, а для единственности решения в этом случае необходимо еще задать температурный режим на концах стержня. Это можно сделать с помощью граничных условий, аналогичных тем, которые были сформулированы для уравнений Пуассона и Лапласа.
Граничное условие I рода (на конце стержня x=0 заданна температура): ![]() .
.
Граничное условие II рода (на конце стержня x=0 задан тепловой поток): ![]() .
.
Граничное условие III рода: ![]() .
.
Для другого конца стержня x=1 правые части граничных условий заменяются соответственно на ψ0(t), ψ1(t), ψ2(t). Заметим, что начальное и граничное условия должны удовлетворять так называемым условиям сопряжения, т.е. при условии I рода u0(0)=φ0(0), при условии II рода u0x(0)=φ1(0), при условии III рода -u0x(0)+λu0(0)=φ2(0). Аналогичные условия сопряжения должны выполнятся и на другом конце стержня x=1.
Сформулируем одну из возможных краевых задач. Найти классическое решение уравнения ![]() , удовлетворяющее начальному условию
, удовлетворяющее начальному условию ![]() и следующим граничным условиям
и следующим граничным условиям ![]() . Эта задача обычно называется первой краевой задачей для уравнения теплопроводности. Соответственно краевые задачи с граничными условиями II роди или III называются второй и третьей краевой задачей для уравнения теплопроводности.
. Эта задача обычно называется первой краевой задачей для уравнения теплопроводности. Соответственно краевые задачи с граничными условиями II роди или III называются второй и третьей краевой задачей для уравнения теплопроводности.
Метод конечных разностей (метод сеток)
Численные методы, основанные на разностной аппроксимации производных называется разностным методом, методом конечных разностей или методом сеток.
Пусть заданно линейное дифференциальное уравнение, записанное в символическом виде: ![]() . Здесь u – искомое решение уравнения; L – некоторый дифференциальный оператор, сокращенно обозначающий соответствующую дифференциальную операцию; f – правая часть уравнения (заданная функция).
. Здесь u – искомое решение уравнения; L – некоторый дифференциальный оператор, сокращенно обозначающий соответствующую дифференциальную операцию; f – правая часть уравнения (заданная функция).
Для единственного решения данного уравнения к нему необходимо присоединить краевые условия: ![]() .
.
Разностный метод решения этих двух задач можно представить в виде двух этапов:
построение разностной схемы, аппроксимирующей данную непрерывную задачу; получение решения разностной задачи и оценка погрешности этого решения.Для построения разностной схемы первым шагом является замена области ![]() непрерывного изменения аргументов областью дискретного их изменения – сеточной областью
непрерывного изменения аргументов областью дискретного их изменения – сеточной областью ![]() , т.е.множеством точек (xn, ym), называемых узлами сетки. Для квадрата
, т.е.множеством точек (xn, ym), называемых узлами сетки. Для квадрата ![]() сеточную область можно построить следующим образом. Проведем прямые
сеточную область можно построить следующим образом. Проведем прямые ![]() . Множество точек пересечения этих прямых и составит сеточную область, а сами точки образуют узлы сетки. Всякая функция
. Множество точек пересечения этих прямых и составит сеточную область, а сами точки образуют узлы сетки. Всякая функция ![]() , определенная на ссеке
, определенная на ссеке ![]() , называется сеточной функцией и обозначается
, называется сеточной функцией и обозначается ![]() .
.
Второй шаг в построении разностной схемы состоит в аппроксимации дифференциального выражения Lu некоторым разностным выражением, а функцию непрерывного аргумента f – сеточной функцией, т.е. в построение некоторого разностного аналога для данного уравнения, при данных краевых условиях.
Такая аппроксимация приводит к системе алгебраических уравнений относительно значений некоторой сеточной функции ![]() . Эту систему можно записать в следующем виде:
. Эту систему можно записать в следующем виде:
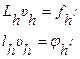
Где Lh и φh – разностные операторы, аппроксимирующие соответственно L и l; υh – искомая сеточная функция, аппроксимирующая решение u; fh, φh – заданные сеточные функции, аппроксимирующие f и φ.
Совокупность разносных уравнений, аппроксимирующих исходную задачу – есть разностная схема. Рассмотрим их подробнее на примерах уравнения теплопроводности и колебания струны.
Разностные схемы для решения уравнения теплопроводности (параболический тип)
Рассмотрим первую краевую задачу для уравнения теплопроводности в прямоугольнике ![]() . Требуется найти непрерывное в
. Требуется найти непрерывное в ![]() решение задачи:
решение задачи:
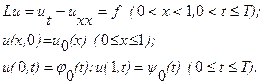
В области ![]() введем прямоугольную равномерную сетку
введем прямоугольную равномерную сетку ![]() {xn, tk} с шагом h=1/N по координате x и с шагом τ=T/M по координате t:
{xn, tk} с шагом h=1/N по координате x и с шагом τ=T/M по координате t:
![]() .
.
Производные левой части уравнения ![]() аппроксимируем следующим разностными выражениями:
аппроксимируем следующим разностными выражениями: 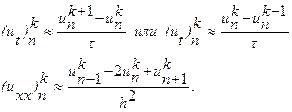
В соответствии с данной аппроксимацией построим два разностных аналога уравнения ![]() с неизвестной сеточной функцией υhτ:
с неизвестной сеточной функцией υhτ: 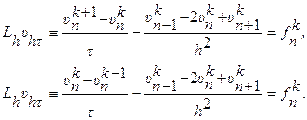
Здесь ![]() - значение некоторой сеточной функции fhτ, соответствующей правой части уравнения
- значение некоторой сеточной функции fhτ, соответствующей правой части уравнения ![]() . Для первой разностной схемы
. Для первой разностной схемы ![]() , а для второй -
, а для второй - ![]() .
.
Начальное и граничное условия для первой краевой задачи аппроксимируются точно: 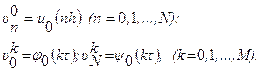
Для второй и третьей краевых задач граничные условия аппроксимируются на основе разностных выражений.
Полагая r=τ/h2 получим ![]() - для первой разностной схемы,
- для первой разностной схемы, ![]() - - для второй разностной схемы.
- - для второй разностной схемы.
Анализ показывает, что погрешность аппроксимации схем есть ![]() .
.
Разностные схемы для решения уравнения колебания струны (гиперболический тип)
Рассмотрим первую краевую задачу для уравнения колебания струны в прямоугольнике ![]() . Требуется найти непрерывное в
. Требуется найти непрерывное в ![]() решение задачи:
решение задачи:

Применение метода конечных разностей к решению задачи по существу мало чем отличается от его применения к уравнению теплопроводности. Область ![]() покрывается сеткой
покрывается сеткой ![]() . Отличие заключается в приближении второй производной по переменной t:
. Отличие заключается в приближении второй производной по переменной t:
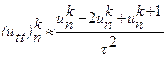 .
.
Разностная аппроксимация принимает вид
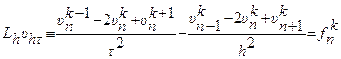 .
.
Начальные условия аппроксимируются следующим образом: 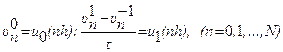 .
.
Граничные условия аппроксимируются точно так же, как и для уравнения теплопроводности: ![]() .
.
Значение ![]() является фиктивным неизвестным, которое можно определить по формуле:
является фиктивным неизвестным, которое можно определить по формуле: ![]() , где γ=τ/h.
, где γ=τ/h.
Анализ показывает, что погрешность аппроксимации схем есть ![]() .
.
Список литературы
Демидович Б.П., Марон И.А. Основы вычислительной математики. Наука, 1970. Минкова Р.М., Вайсбурд Р.А. Методы вычислительной математики. УПИ, 1981. Боглаев Ю.П. Вычислительная математика и программирование. Высшая школа, 1990. Кацман Ю.Я. Прикладная математика. Численные методы. ТПУ, 2000.Похожие работы
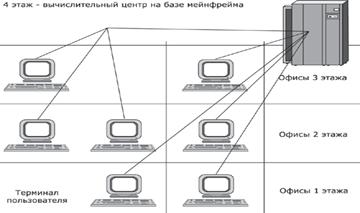
... в какой-то степени являлись прообразом современных компьютерных сетей (рис.1.2), а соответствующее системное программное обеспечение — прообразом сетевых операционных систем. Рис. 1.2 Многотерминальная система — прообраз вычислительной сети Многотерминальные централизованные системы уже имели все внешние признаки локальных вычислительных сетей, однако по существу ими не являлись, так как ...
... ; - показывать, за счет каких структурных особенностей достигается увеличение производительности различных вычислительных систем; с этой точки зрения, классификация может служить моделью для анализа производительности. 1.12 Классификация Дазгупты Одним из последних исследований по классификации архитектур, по-видимому, является работа С. Дазгупты, вышедшая в 1990 году. Автор ...
... ? 8. Какими программами можно воспользоваться для устранения проблем и ошибок, обнаруженных программой Sandra? Раздел 3. Автономная и комплексная проверка функционирования и диагностика СВТ, АПС и АПК Некоторые из достаточно интеллектуальных средств вычислительной техники, такие как принтеры, плоттеры, могут иметь режимы автономного тестировании. Так, автономный тест принтера запускается без ...
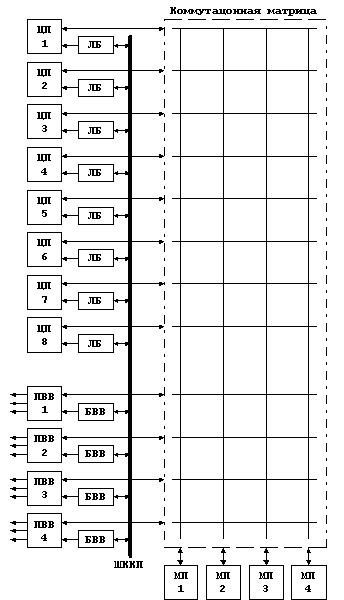
... процесса, а либо вообще не сказываются на работе МПВК, либо вызывают постепенную деградацию вычислительной мощности. Меры по обеспечению отказоустойчивости свои для каждого компонента МПВК. Отказы оперативной памяти были рассмотрены выше. Отказы в коммутационной матрице также как и отказы оперативной памяти целесообразно маскировать применением кодов, корректирующих ошибки. Наиболее сложны для ...
0 комментариев