Навигация
План чтения лекции по учебной дисциплине «Математические методы»
Юридический техникум Рассмотрено и одобрено ПЦК
г. Кропоткин программирования
Председатель ПЦК
Покалицына О.В.
План
чтения лекции по учебной дисциплине
«Математические методы»
Раздел № 2. Линейное программирование.
Тема № 2.2. Основная задача линейного программирования.
Занятие №
Место проведения: аудитория.
Литература:
1. Венцель Е.С. Исследование операций. Задач, принципы, методология. – М.: Наука, 1980.
2. Шелобаев С.И. Математические методы и модели в экономике, финансах, бизнесе. – М.:ЮНИТИДАНА, 2001
Учебные вопросы и расчет времени
| №п/п | Учебные вопросы | Время, мин | Методические указания |
| 1. 2. | Основная задача ЛП (ОЗЛП). Существование решения. |
1. Вводная часть. Организационный момент. План занятия. Основные требования.
2. Основная часть.
1. Основная задача ЛП (ОЗЛП).
Любую задачу линейного программирования можно свести к стандартной форме, так называемой «основной задаче линейного программирования» (ОЗЛП), которая формируется так: найти неотрицательные значения переменные x1, x2, …, xn, которые удовлетворяли бы условиям – равенствам:
a11 x1 + a12 x2 + … +a1n xn = b1,
a21 x1 + a22 x2 + … +a2n xn = b2, (6.1.)
………………………………..
am1 x1 +am2 x2 + … +amn xn = bm.
и обращали бы в максимум линейную функцию этих переменных:
![]() (6.2.)
(6.2.)
Случай, когда L надо обратить не в максимум, а в минимум, легко сводится к простому: изменить знак L на обратный (максимизировать не L, а L`=-L). Кроме того, от любых условий – неравенств можно перейти к условиям – равенствам ценой введения некоторых новых «дополнительных» переменных. Пусть требуется найти неотрицательные значения переменных x1,x2,x3, удовлетворяющие ограничениям – неравенствам
![]() (6.3.)
(6.3.)
![]()
и обращающие в максимум линейную функцию от этих переменных:
![]() (6.4.)
(6.4.)
Начнём с того, что приведём условия (6.3.) к стандартной форме, так, чтобы знак неравенства был ³, а справа стоял нуль. Получим:
![]() (6.5.)
(6.5.)
![]()
А теперь обозначим левые части неравенств (6.5.) соответственно через y1 и y2:
![]() (6.6.)
(6.6.)
![]()
Из условий (6.5.) и (6.6.) видно, что новые переменные y1, y2 также должны быть неотрицательными.
Какая же теперь перед нами стоит задача? Найти неотрицательные значения переменных x1,x2,x3,y1,y2 такие, чтобы они удовлетворяли условиям – равенствам (6.6.) и обращали в максимум линейную функцию этих переменных (то, что в L не входит дополнительные переменные y1, y2, неважно: можно считать, что они входят, но с нулевыми коэффициентами). Перед нами – основная задача линейного программирования (ОЗЛП). Переход к ней от первоначальной задачи с ограничениями – неравенствами (6.3.) «куплен» ценой увеличения числа переменных на два (число неравенств).
2. Существование решения ОЗЛП и способы его нахождения.
Рассмотрим основную задачу линейного программирования (ОЗЛП): найти неотрицательные значения переменных x1, x2, …, xn, удовлетворяющие m условиям – равенствам:
a11 x1+a12 x2+…+a1n xn=b1,
a21 x1+a22 x2+…+a2n xn=b2, (7.1.)
…………………………...
am1 x1+am2 x2+…+amn xn=bm
и обращающие в максимум линейную функцию этих переменных:
![]() (7.2.)
(7.2.)
Для простоты предположим, что все условия (7.1.) линейно независимы (r=m), и будем вести рассуждения в этом предположении.
Назовём ДОПУСТИМЫМ решением ОЗЛП всякую совокупность неотрицательных значений x1, x2, …, xn, удовлетворяющую условиям (7.1.).
ОПТИМАЛЬНЫМ назовём то из допустимых решений, которое обращает в максимум функцию (7.2.).
Требуется найти оптимальное решение. Всегда ли эта задача имеет решение? Нет, не всегда.
Похожие работы
... xij, удовлетворяющих поставленным ограничениям. Клетки с не нулевыми перевозками называются базисными, а с нулевыми – свободными. В зависимости от соотношения между запасами и заявками транспортная задача называется сбалансированной или несбалансированной. Сбалансированная ТЗ: Несбалансированная ТЗ: Для сбалансированной ТЗ ограничения принимают вид равенств, то есть получаем m+n ограничений, ...
... , финансах, бизнесе. – М.:ЮНИТИДАНА, 2001 Учебные вопросы и расчет времени №п/п Учебные вопросы Время, мин Методические указания 1. 2. 3. 4. Введение. Оптимальное решение. Основные понятия и определения оптимизации. Постановка задачи оптимизации в общей форме. 1. Вводная часть. Организационный момент. План занятия. Основные требования. 2. Основная часть. ...
... Основная часть. 1. Задача линейного программирования (ЗЛП). Термин линейное программирование появился в Америке в середине 40-х годов (первая американская работа по частной задаче линейного программирования опубликована в 1941 г.). В Советском Союзе исследования в этой области начались ранее. В конце 30-х годов целый ряд существенных результатов по линейному программированию был установлен ...
... . 4 1 - 3 9 Статистическое изучение динамики правовых явлений (ряды динамики в правовой статистике). 4 - - 4 10 Статистические методы изучения взаимосвязей. Комплексный статистический анализ. 4 - - 4 ИТОГО: 40 6 2 32 2.3 Учебная программа дисциплины Содержание лекционного курса Тема 1. Общее понятие статистики и ее отраслей. Современная организация статистики в ...
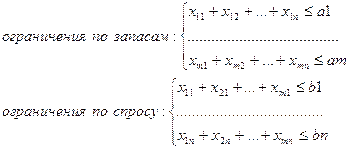
0 комментариев