Навигация
Понятие величины и её измерения в математике
1.2. Понятие величины и её измерения в математике.
Длина, площадь, масса, время, объём - величины. Первоначальное знакомство с ними происходит в начальной школе, где величина наряду с числом является ведущим понятием.
ВЕЛИЧИНА - это особое свойство реальных объектов или явлений, и особенность заключается в том, что это свойство можно измерить, то есть назвать количество величины, которые выражают одно и тоже свойство объектов, называются величинами одного рода или однородными величинами. Например, длина стола и дли на комнаты - это однородные
величины. Величины - длина, площадь, масса и другие обладают рядом свойств.
1)Любые две величины одного рода сравнимы: они либо равны, либо одна меньше (больше) другой. То есть, для величин одного рода имеют место отношения «равно», «меньше», «больше» и для любых величин и справедливо одно и только одно из отношений: Например, мы говорим, что длина гипотенузы прямоугольного треугольника больше, чем любой катет данного треугольника; масса лимона меньше, чем масса арбуза; длины противоположных сторон прямоугольника равны.
2)Величины одного рода можно складывать, в результате сложения получится величина того же рода. Т.е. для любых двух величин а и b однозначно определяется величина a+b, её называют суммой величин а и b. Например, если a-длина отрезка AB, b - длина отрезка ВС (рис.1), то длина отрезка АС, есть сумма длин отрезков АВ и ВС;
. 3)Величину умножают на действительное число, получая в результате величину того же рода. Тогда для любой величины а и любого неотрицательного числа x существует единственная величина b= x а, величину b называют произведением величины а на число x. Например, если a - длину отрезка АВ умножить на
x= 2, то получим длину нового отрезка АС .(Рис.2)
4) Величины данного рода вычитают, определяя разность величин через сумму:
разностью величин а и b называется такая величина с, что а=b+c. Например, если а - длина отрезка АС, b - длина отрезка AB, то длина отрезка ВС есть разность длин отрезков и АС и АВ.
5) Величины одного рода делят, определяя частное через произведение величины на число; частным величин а и b-называется такое неотрицательное действительное число х, что а= х b. Чаще это число - называют отношением величин а и b и записывают в таком виде: a/b = х. Например, отношение длины отрезка АС к длине отрезка АВ равно 2.(Рис №2).
6) Отношение «меньше» для однородных величин транзитивно: если А<В и В<С, то А<С. Так, если площадь треугольника F1 меньше площади треугольника F2 площадь треугольника F2 меньше площади треугольника F3, топлощадь треугольника F1 меньше площади треугольника F3. Величины, как свойства объектов, обладают ещё одной особенностью - их можно оценивать количественно. Для этого величину нужно измерить. Измерение - заключается в сравнении данной величины с некоторой величиной того же рода, принятой за единицу. В результате измерения
получают число, которое называют численным значением при выбранной единице.
Процесс сравнения зависит от рода рассматриваемых величин: для длин он один, для площадей - другой, для масс- третий и так далее. Но каким бы ни был этот процесс, в результате измерения величина получает определённое численное значение при выбранной единице.
Вообще, если дана величина а и выбрана единица величины e, то в результате измерения величины а находят такое действительное число x, что а=x e. Это число x называют численным значением величины а при единице е. Это можно записать так: х=m (a).
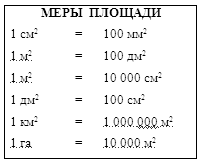
Согласно определению любую величину можно представить в виде произведения некоторого числа и единицы этой величины. Например, 7 кг = 7 1 кг, 12 см =12 1 см, 15ч =15 1 ч. Используя это, а также определение умножения величины на число, можно обосновать процесс перехода от одной единицы величины к другой. Пусть, например, требуется выразить 5/12ч в минутах. Так как, 5/12ч = 5/12 60мин = (5/12 60)мин = 25мин.
Величины, которые вполне определяются одним численным значением, называются скалярными величинами. Такими, к примеру, являются длина, площадь, объём, масса и другие. Кроме скалярных величин, в математике рассматривают ещё векторные величины. Для определения векторной величины необходимо указать не только её численное значение, но и направление. Векторными величинами являются сила, ускорение, напряжённость электрического поля и другие.
В начальной школе рассматриваются только скалярные величины, причём такие, численные значения которых положительны, то есть положительные скалярные величины.
Измерение величин позволяет свести сравнение их к сравнению чисел, операции над величинами к соответствующим операциям над числами.
1/.Если величины а и b измерены при помощи единицы величины e, то отношения между величинами a и b будут такими же, как и отношения между их численными значениями, и наоборот.
![]() a=b m (a)=m (b),
a=b m (a)=m (b),
![]() a>b m (a)>m (b),
a>b m (a)>m (b),
![]() a<b m (a)<m (b).
a<b m (a)<m (b).
Например, если массы двух тел таковы, что а=5 кг, b=3 кг, то можно утверждать, что масса а больше массы b поскольку 5>3.
2/ Если величины а и b измерены при помощи единицы величины e, то, чтобы найти численное значение суммы a+b достаточно сложить
численные значения величин а и b. а+b= c m (a+b) = m (a) + m (b). Например, если а = 15 кг, b=12 кг, то а+b=15 кг + 12 кг = (15+12) кг = 27кг
З/ Если величины а и b таковы, что b= x а, где x -положительное действительное число, и величина а, измерена при помощи единицы величины e, то чтобы найти численное значение величины b при единице e, достаточно число x умножить на число m (а):b=x a m (b)=x m (a).
Например, если масса а в 3 раза больше массы b .т.е. b= За и а = 2 кг, то
b= За=3 (2 кг) = (3 2) кг = 6кг.
Рассмотренные понятия - объект, предмет, явление, процесс, его величина, численное значение величины, единица величины - надо уметь вычленять в текстах и задачах.
Например, математическое содержание предложения «Купили 3 килограмма яблок» можно описать следующим образом: в предложении рассматривается такой объект, как яблоки, и его свойство - масса; для измерения массы использовали единицу массы - килограмм; в результате измерения получили число 3 -численное значение массы яблок при единице массы - килограмм.
Рассмотрим определения некоторых величин и их измерений.
Длина отрезка и её измерение.
Длиной отрезка называется положительная величина, определённая для каждого отрезка так что:
1/ равные отрезки имеют разные длины;
2/ если отрезок состоит из конечного числа отрезков, то его длина равна сумме длин этих отрезков.
Рассмотрим процесс измерения длин отрезков. Из множества отрезков выбирают какой-нибудь отрезок e и принимают его за единицу длины. На отрезке а от одного из его концов откладывают последовательно отрезки равные e, до тех пор, пока это возможно. Если отрезки, равные e отложились n раз и конец последнего совпал с концом отрезка e, то говорят, что значение длины отрезка а есть натуральное число n, и пишут: а = ne. Если же отрезки, равные e, отложились n раз и остался ещё остаток, меньший e, то на нём откладывают отрезки равные e =1/10e. Если они отложились точно n раз, то тогда а=n, n e и значение длины отрезка а есть конечная десятичная дробь. Если же отрезок e отложился n раз и остался ещё остаток, меньший e , то на нём откладывают отрезки, равные e =1/100e. Если представить этот процесс бесконечно продолженным, то получим, что значение длины отрезка а есть бесконечная десятичная дробь.
Итак, при выбранной единице, длина любого отрезка выражается действительным числом. Верно и обратное; если дано положительное действительное число n, n , n , ... то взяв его приближение с определённой
точностью и проведя построения, отражённые в записи этого числа, получим отрезок, численное значение длины которого, есть дробь: n ,n ,n …
Площадь фигуры и её измерение.
Понятие о площади фигуры имеет любой человек: мы говорим о площади комнаты, площади земельного участка, о площади поверхности, которую надо покрасить, и так далее. При этом мы понимаем, что если земельные участки одинаковы, то площади их равны; что у большего участка площадь больше; что площадь квартиры слагается из площади комнат и площади других её помещений.
Это обыденное представление о площади используется при её определении в геометрии, где говорят о площади фигуры. Но геометрические фигуры устроены по-разному, и поэтому когда говорят о площади, выделяют особый класс фигур. Например, рассматривают площади многоугольников и других ограниченных выпуклых фигур, или площадь круга, или площадь поверхности тел вращения и так далее. В начальном курсе математики рассматриваются только площади многоугольников и ограниченных выпуклых плоских фигур. Такая фигура может быть составлена из других. Например, фигура F, (рис.4), составлена из фигур F1, F2, F3. Говоря, что фигура составлена (состоит) из фигур F1, F2,…,Fn, имеют в виду, что она является их объединением и любые две данные фигуры не имеют общих внутренних точек. Площадью фигуры называется неотрицательная величина, определённая для каждой фигуры так, что:
I/ равные фигуры имеют равные площади;
2/ если фигура составлена из конечного числа фигур, то её площадь равна сумме их площадей. Если сравнить данное определение с определением длины отрезка, то увидим, что площадь характеризуется теми же свойствами, что и длина, но заданы они на разных множествах: длина - на множестве отрезков, а площадь - на множестве плоских фигур. Площадь фигуры F обозначать S(F). Чтобы измерить площадь фигуры, нужно иметь единицу площади. Как правило, за единицу площади принимают площадь квадрата со стороной, равной единичному отрезку e, то есть отрезку, выбранному в качестве единицы длины. Площадь квадрата со стороной e обозначают e . Например, если длина стороны единичного квадрата m, то его площадь m .
Измерение площади состоит в сравнении площади данной фигуры с площадью единичного квадрата e. Результатом этого сравнения является такое число x, что S(F)=x e .Число x называют численным значением площади при выбранной единице площади.
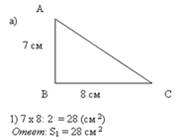
Так, если единицей площади является см, то площадь фигуры, приведённой на рисунке 5, равна 5см.
Рассмотрим один из приёмов, опирающихся непосредственно на определение площади, является измерение площади при помощи палетки- сетки квадратов, нанесённый на прозрачный материал.
Допустим, на фигуру F . площадь которой надо измерить, наложена сетка квадратов со стороной e. Тогда по отношению к этой фигуре можно выделить квадраты двух видов:
1/ квадраты, которые целиком лежат внутри фигуры F.
2/ квадраты, через которые проходит контур фигуры, и которые лежат частью вне фигуры F.
Пусть квадратов первого вида окажется m, а квадратов второго вида n. Тогда, очевидно, площадь фигуры F будет удовлетворять условию.
m <S(F)<(m+n) . Числа m и m+n будут приближёнными численными значениями измеряемой площади: первое число с недостатком, второе - с избытком.
Как видим, что палетка позволяет измерить площадь фигуры лишь с невысокой точностью. Чтобы получить более точный результат, можно уплотнить первоначальную сеть квадратов, разделив каждый из них на более мелкие квадраты. Можно, например, построить сеть квадратов со стороной e =1/10e.
В результате мы с большой точностью получим другие приближенные значения площади фигуры F.
Описанный процесс можно продолжить. Возникает вопрос: существует ли такое действительное число, которое больше всякого приближённого результата измерения, взятого с избытком, и которое может быть точным численным значением измеряемой площади? В математике доказано, что при выбранной единице площади такое число существует для всякой площади, оно единственно и удовлетворяет свойствам 1 и 2.
Масса и её измерение.
Масса - одна из основных физических величин. Понятие массы тела тесно связано с понятием веса-силы, с которой тело притягивается Землёй. Поэтому вес тела зависит не только от самого тела. Например, он различен на разных широтах: на полюсе тело весит на 0,5 % больше, чем на экваторе. Однако при своей изменчивости вес обладает особенностью: отношение весов двух тел в любых условиях остаётся неизменным. При измерении веса тела путём сравнения его с весом другого выявляется новое свойство тел, которое называется массой. Представим, что на одну из чашек рычажных весов положили какое-нибудь тело, а на другую чашку положили второе тело b. При этом возможны случаи:
1) Вторая чашка весов опустилась, а первая поднялась так, что они оказались в результате на одном уровне. В этом случае говорят, что весы находятся в равновесии, а тела а и b имеют равные массы.
2) Вторая чашка весов так и осталась выше первой. В этом случае говорят, что масса тела а больше массы тела b.
3) Вторая чашка опустилась, а первая поднялась и стоит выше второй. В этом случае говорят, что масса тела а меньше тела b.
С математической точки зрения масса - это такая положительная величина, которая обладает свойствами:
1) Масса одинакова у тел, уравновешивающих друг друга на весах;
2) Масса складывается, когда тела соединяются вместе: масса нескольких тел, вместе взятых равна сумме их масс. Если сравнить данное определение с определениями длины и площади, то увидим, что масса характеризуется теми же свойствами, что длина и площадь, но задана на множестве физических тел.
Измерение массы производится с помощью весов. Происходит это следующим образом. Выбирают тело e, масса которого принимается за единицу. Предполагается, что можно взять и доли этой массы. Например, если за единицу массы взят килограмм, то в процессе измерения можно использовать такую его долю, как грамм: 1г= 0,01кг.
На одну чашку весов кладут тело, массу тела кого того измеряют, а на другую – тела, выбранные в качестве единицы массы, то есть гири. Этих гирь должно быть столько, чтобы они уравновесили первую чашку весов. В результате взвешивания получается численное значение массы данного тела при выбранной единице массы. Это значение приближённое. Например, если масса тела равна 5 кг 350 г, то число 5350следует рассматривать как значение массы данного тела ( при единице массы – грамм). Для численных значений массы справедливы все утверждения, сформулированные для длины, то есть сравнение масс, действия над ними сводятся к сравнению и действиям над численными значениями масс (при одной и той же единице массы).
Основная единица массы - килограмм. Из этой основной единицы образуются другие единицы массы: грамм, тонна и другие.
Промежутки времени и их измерение.
Понятие времени более сложное, чем понятие длины и массы. В обыденной жизни время - это то, что отделяет одно событие от другого. В математике и физике время рассматривают как скалярную величину,
потому что промежутки времени обладают свойствами, похожими на свойства длины, площади, массы.
Промежутки времени можно сравнивать. Например, на один и тот же путь пешеход затратит больше времени, чем велосипедист.
Промежутки времени можно складывать. Так, лекция в институте длится столько же времени, сколько два урока в школе.
Промежутки времени измеряют. Но процесс измерения времени отличается от измерения длины, площади или массы. Для измерения длины можно многократно использовать линейку, перемещая её с точки на точку. Промежуток времени, принятый за единицу, может быть использован лишь один раз. Поэтому единицей времени должен быть регулярно повторяющийся процесс. Такой единицей в Международной системе единиц названа секунда. Наряду с секундой используются и другие единицы времени: минута, час, сутки, год, неделя, месяц, век. Такие единицы, как год и сутки, были взяты из природы, а час, минута, секунда придуманы человеком.
Год - это время обращения Земли вокруг Солнца. Сутки - это время обращения Земли вокруг своей оси. Год состоит приблизительно из 365 суток. Но год жизни людей складывается из целого числа суток. Поэтому вместо того, чтобы к каждому году прибавлять 6 часов, прибавляют целые сутки к каждому четвёртому году. Этот год состоит из 366 дней и называется високосным.
В Древней Руси неделя называлась седмицей, а воскресенье - днём недельным (когда нет дел) или просто неделей, т.е. днём отдыха. Названия следующих пяти дней недели указывают, сколько дней прошло после воскресенья. Понедельник - сразу после неделя, вторник - второй день, среда - середина, четвёртые и пятые сутки соответственно четверг и пятница, суббота - конец дел.
Месяц не очень определённая единица времени, он может состоять из тридцати одного дня, из тридцати и двадцати восьми, двадцати девяти в високосные годы (дней). Но существует эта единица времени с древних времён и связана с движением Луны вокруг Земли. Один оборот вокруг
Земли Луна делает примерно за 29,5 суток, и за год она совершает примерно 12 оборотов. Эти данные послужили основой для создания древних календарей, а результатом их многовекового усовершенствования является тот календарь, которым мы пользуемся и сейчас.
Так как Луна совершает 12 оборотов вокруг Земли, люди стали считать полнее число оборотов (то есть 22) за год, то есть год – 12 месяцев.
Современное деление суток на 24 часа также восходит к глубокой древности, оно было введено в Древнем Египте. Минута и секунда появились в Древнем Вавилоне, а в том, что в часе 60 минут, а в минуте 60 секунд, сказывается влияние шестидесятеричной системы счисления,
изобретённой вавилонскими учёными.
Объём и его измерение.
Понятие объёма определяется так же, как понятие площади. Но при рассмотрение понятия площадь, мы рассматривали многоугольные фигуры, а при рассмотрении понятия объём мы будем рассматривать многогранные Фигуры.
Объёмом фигуры называется неотрицательная величина, определённая для каждой Фигуры так, что:
1/равные фигуры имеют один и тот же объём;
2/если фигура составлена из конечного числа фигур, то её объём равен сумме их объёмов.
Условимся объём фигуры F обозначать V(F).
Чтобы измерить объем фигуры, нужно иметь единицу объёма. Как правило, за единицу объёма принимают объём куба с гранью, равной единичному отрезку e, то есть отрезку, выбранному в качестве единицы длины.
Если измерение площади сводилось к сравнению площади данной фигуры с площадью единичного квадрата e , то, аналогично, измерение объёма данной фигуры состоит в сравнении его с объёмом единичного куба е3 ( рис.б ). Результатом этого сравнения является такое число x, .что V(F)=х е.Число х называют численным значением объёма при выбранной единице объёма.
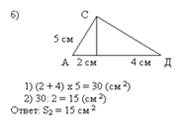
Так. если единицей объёма является 1 см, то объём фигуры, приведённой на рисунке 7, равен 4 см.
ГЛАВА 2.Методика формирования понятия величины и её измерения у младших школьников.
Похожие работы
... в форме выступления с докладом на научно-практической конференции на тему: "Актуальные проблемы методики изучения математики в начальных классах" (11.03.2010 г). По результатам исследования написана статья "Особенности изучения нумерации многозначных чисел в начальных классах". Достоверность результатов исследования определяется анализом теоретического и экспериментального материала, методами ...
... в том, что узнали, чему научились, что удалось, кому и над чем надо поработать. Это способствует развитию у детей самоконтроля, умения правильно оценивать свои знания и действия. Программа описываемого курса рассчитана на детей 5-6,5 лет и может быть реализована при проведении занятий 2 раза в неделю, в течение года 72 занятия. Продолжительность одного занятия – 30 минут. Учебно-тематическое ...
... учащихся, школьную документацию, сделать выводы о степени усвоения данного понятия. Подвести итог об исследовании особенностей математического мышления и процесса формирования понятия комплексного числа. Описание методов. Диагностические: I этап. Беседа проводилась с учителем математики, которая в 10Є классе преподает алгебру и геометрию. Беседа состоялась по истечении некоторого времени с начала ...
... и обобщение опыта учителей при проведении уроков математики по данной теме. Курсовая работа состоит из введения, двух глав, заключения, списка литературы. Глава I. Методические особенности изучения площади геометрических фигур и единиц ее измерения на уроках математики в начальной школе 1.1 Возрастные особенности развития младших школьников на этапе формирования геометрических представлений ...

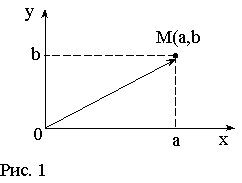

0 комментариев