Навигация
Знаходять критичні точки в інтервалі (a;b) (точки, в яких похідна дорівнює нулю або не існує), обчислюють значення функції в цих точках;
1. знаходять критичні точки в інтервалі (a;b) (точки, в яких похідна дорівнює нулю або не існує), обчислюють значення функції в цих точках;
2. знаходять значення функції на кінцях відрізка, тобто![]() ;
;
3. серед усіх значень вибирають найбільше і найменше значення.
У випадку, коли функція монотонна на відрізку [a;b], то найбільшого і найменшого значення вона досягає на кінцях відрізка. У цьому випадку обмежуємось обчисленням значень ![]() .
.
По-іншому складається ситуація, якщо необхідно знайти найбільше та найменше значення функції, неперервної в інтервалі (a;b).
Зрозуміло, що функція у цьому випадку не може досягати найбільшого і найменшого значення на кінцях інтервалу. Наприклад, функція ![]() в інтервалі (3;6) не має ні найбільшого, ні найменшого значення у внутрішніх точках інтервалу. У цьому випадку чинять так:
в інтервалі (3;6) не має ні найбільшого, ні найменшого значення у внутрішніх точках інтервалу. У цьому випадку чинять так:
1. знаходять критичні точки, що належать цьому інтервалу, і обчислюють значення функції в цих точках;
2. знаходять ліву та праву границі відповідно в точках а і б , тобто ![]() . Якщо ці границі існують, то їх порівнюють із значеннями функції в критичних точках. Якщо виявиться, що значення в критичних точках більші(менші) за знайдені границі, то це і буде найбільшим(найменшим) значенням функції на інтервалі.
. Якщо ці границі існують, то їх порівнюють із значеннями функції в критичних точках. Якщо виявиться, що значення в критичних точках більші(менші) за знайдені границі, то це і буде найбільшим(найменшим) значенням функції на інтервалі.
Приклади.
Приклад 1. Знайти найбільше та найменше значення функції на відрізку [a;b]
![]()
Розв’язання. На даному відрізку функція визначена і неперервна, диференційована в інтервалі(-2;2). Знайдемо похідну, критичні точки:
![]()
![]() х=0
х=0
знайдемо значення функції в критичній точці і на кінцях відрізка:
![]()
Отже,
![]()
![]() .
.
Приклад 2. Знайти найбільше та найменше значення функції на відрізку [a;b]
![]()
Розв’язання. Функція визначена і неперервна на відрізку ![]() , диференційна в інтервалі (-1;1). Тому вона набуває на даному відрізку найбільшого і найменшого значення. Знайдемо критичні точки даної функції. Для цього знайдемо похідну
, диференційна в інтервалі (-1;1). Тому вона набуває на даному відрізку найбільшого і найменшого значення. Знайдемо критичні точки даної функції. Для цього знайдемо похідну
![]()
і прирівняємо її до нуля:
х4+8х=0; х=0; х=-2.
Отже, на інтервалі (-1;1)функція має лише одну критичну точку х=0. знайдемо значення функції в цій точці ![]() .
.
Обчислимо значення функції на кінцях відрізка
![]() ,
, ![]() .
.
Отже,
![]() ,
, ![]()
Відповідь:![]() ,
,![]()
1.5. Означення дотичної, піддотичної, нормалі
Нехай функція y=f(x) диференційована в точці х0. рівняння дотичної до графіка функції y=f(x) в цій точці має такий вигляд:
![]() ,
,
де х і у – біжучі координати дотичної, f ‘(x0)=k – кутовий коефіцієнт дотичної, який дорівнює значенню похідної в точці х0, тобто тангенс кута нахилу дотичної до доданого напрямку осі абсцис.
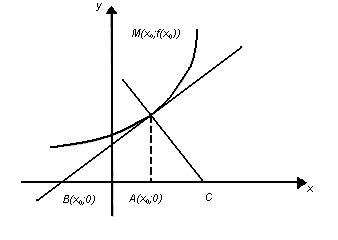
Відрізок АВ, що міститься між абсцисою точки дотику і точкою перетину дотичної з віссю абсцис, називають під дотичною. Її довжина дорівнює |х0-х1|.
Пряма МС, перпендикулярна до дотичної в точці її дотику М до графіка функції у=f(x), називається нормаллю.
Рівняння нормалі записують у вигляді:
![]()
якщо f ‘(x0)![]() 0(в противному разі рівняння нормалі х-х0=0).
0(в противному разі рівняння нормалі х-х0=0).
На цей матеріал можна скласти ряд задач. Розглянемо деякі з них.
1. Дано абсцису точки дотику х0 графіка функції у=f(x), а необхідно записати рівняння дотичної, що проходить через точку з цією абсцисою.
Для цього знаходимо похідну функції у=f(x), її значення в точці х0, тобто ![]() , та значення функції в точці х0, тобто
, та значення функції в точці х0, тобто ![]() . Цих даних достатньо, щоб записати рівняння дотичної
. Цих даних достатньо, щоб записати рівняння дотичної ![]() .
.
2. Який кут утворює дотична з додатним напрямком осі абсцис, якщо відома абсциса точки дотику х0?
Оскільки кутовий коефіцієнт дотичної ![]() ,то
,то ![]() .
.
Таким чином, задача зводиться до знаходження похідної функції у=f(x), тобто y’=f ‘(x), і обчислення її значення в точці х0.
3. Знайти гострий кут між дотичними, проведеними до графіків функцій ![]() ,що мають спільну абсцису х0:
,що мають спільну абсцису х0:
![]()
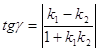 ,
, 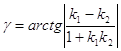 .
.
4. Знайти довжину дотичної до графіка функції у=f(x), абсциса точки дотику якої дорівнює х0.
Довжиною дотичної прийнято називати відстань між точкою дотику до графіка функції і точкою її перетину з віссю абсцис.
У цьому випадку знаходимо
![]()
і скористаємося формулою
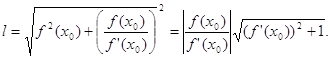
Приклади:
Приклад 1. Знайти рівняння дотичної до графіка функції
![]()
в точці з абсцисою х0=3.
Розв’язання. Знайдемо похідну функції, значення функції та її похідної в точці х0:
![]()
скориставшись рівнянням дотичної
![]() ,
,
матимемо
![]()
Звідси ![]() .
.
Відповідь:![]() .
.
Приклад 2. Який кут з віссю абсцис утворює дотична до параболи y=x2-4x+8 в точці (3;5)?
Розв’язання. Безпосередньо підстановкою координат заданої точки в рівняння параболи переконуємося, що вона їй належить.
Знайдемо похідну y’=2x-4.
Тоді ![]() . Звідси
. Звідси ![]()
Відповідь:![]()
Приклад 3. Дотична до графіка функції
![]()
нахилена до осі абсцис під кутом ![]() . Знайти координати точки дотику.
. Знайти координати точки дотику.
Розв’язання. Знайдемо похідну функції![]() :
:
![]() .
.
За умовою y’(x0)=tg![]() =1 маємо
=1 маємо
![]()
отже, дотична до параболи проходить через точку А(2;2).
Відповідь: А(2;2).
Розділ 2
Застосування похідної
2.1. Правила диференціюванняТеорема: Якщо функції u(x) і n(x) мають похідні у всіх точках інтервалу (a; b), то
(u(x)±(x))’ = u’(x)±n’(x)
для любого х є (a; b). Коротше,
(u±n)’ = u±n’
Доведення: Суму функцій u(x)+n(x), де х є (a; b), яка представляє собою нову функцію, позначимо через f(x) і знайдемо похідну цієї функції,
Нехай х0 – деяка точка інтервалу (a; b).
Тоді 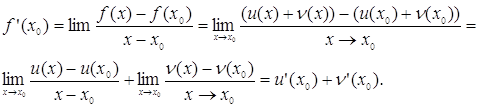
![]()
Також, ![]()
Так як
х0 – допустима точка інтервалу (a; b), то маємо:
![]()
Випадок добутку розглядається аналогічно. Теорема доведена.
Наприклад,
а) ![]()
б) ![]()
в) ![]()
Зауваження. Методом математичної індукції доводиться справедливість формули (u1(x) + u2 (x) +… кінцевого числа складених.
Теорема. Якщо функції u(x) і n(x) мають похідні у всіх точках інтервалу (a; b), то
![]()
для любого х є (a; b). Коротше,
![]()
Доведення. Позначимо похідні ![]() через
через ![]() х є (a; b), і найдемо похідну цієї функції, виходячи із визначення.
х є (a; b), і найдемо похідну цієї функції, виходячи із визначення.
Нехай х0 – деяка точка інтервалу (a; b). Тоді
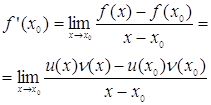
Навіть так як
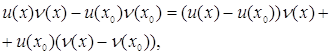
то
![]()
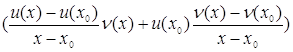
![]()
Так як х0 – вільна точка інтервалу (a; b), то маємо
![]()
Теорема доведена.
Приклад,
а) 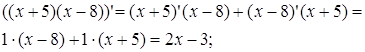
![]()
![]()
б) ![]()
![]()
в) 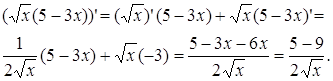
Наслідок. Постійний множник можна виносити за знак похідної:
![]()
Доведення. Застосувавши множник можна виносити за знак теорему про похідну де а – число, отримаємо
![]()
Приклади.
а) ![]()
б) ![]()
Похідна частки двох функцій .
Теорема. Якщо функції ![]() мають похідні у всіх точках інтервалу (a; b), причому
мають похідні у всіх точках інтервалу (a; b), причому ![]() для любого х є (a; b), то
для любого х є (a; b), то
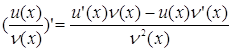
для любого х є (a; b).
![]()
Доведення. Позначимо тимчасово ![]() через
через ![]() знайдемо
знайдемо ![]() використовуючи визначення похідної.
використовуючи визначення похідної.
Нехай х0 – деяка точка інтервалу (a; b).
Тоді,
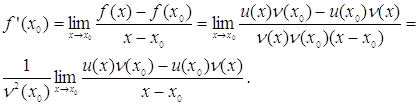
Навіть, так як
![]() то
то
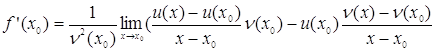
і послідовно
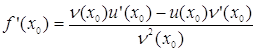
Так як х0 – вільна точка інтервалу (a; b), то в останній формулі х0 можна замінити на х. Теорема доведена.
Приклади.
а) 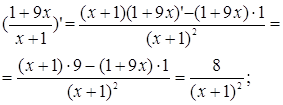
б) 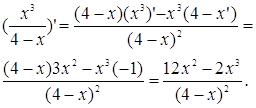
Похожие работы
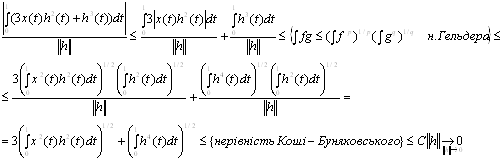
... говорять про похідну за напрямком , розуміючи під цим границю відношення при умові, що вона існує; цю границю позначають . Ясно, що , де – одиничний вектор напрямку , тобто . Зауваження. Похідна Фреше і похідна за напрямком є елементами різної природи: є лінійний оператор з X в Y, в той час як є елементом простору Y. Якщо відображення диференційовне в точці за Фреше, то воно диференційовне ...
... запам’ятовуванню за рахунок активізації декількох аналізаторів: слуху, зору та підтримання постійного контакту з учнями під час уроку. ЛІТЕРАТУРА Махмутов М. Й. Проблемноє обучение. -М.: Педагогика, 1975. – 240 с. Методи обучения математике / Под ред. А. А. Столяра. –Минск.: Висш. шк.,1981. – 398 с. Г.П.Бевз. Методика викладання математики. 3-видання. -К.: Вища школа, 1989. – 352 с. Н.В. ...
... нтуватися на використання підручників [53; 54; 5]. У класах фізико-математичного спрямування доцільно орієнтуватись на використання підручників [53; 54; 5; 1]. РОЗДІЛ 2 ОСОБЛИВОСТІ ВИВЧЕННЯ МАТЕМАТИКИ У ПРОФІЛЬНИХ КЛАСАХ В СУЧАСНИХ УМОВАХ 2.1. ОСНОВНІ ПОЛОЖЕННЯ ПРОФІЛЬНОЇ ДИФЕРЕНЦІАЦІЇ НАВЧАННЯ МАТЕМАТИКИ Математика є універсальною мовою, яка широко застосовується в усіх ...
... може бути компетентною або некомпетентною в певних питаннях, тобто мати компетентність (компетентності) у певній галузі діяльності. Саме тому, одним із результатів навчання курсу «Застосування ІКТ у навчальному процесі з математики» вбачається формування в майбутніх вчителів відповідних ключових фахових компетентностей. Зазначене вище наштовхнуло на дослідження компетентностей: внаслідок чого ...
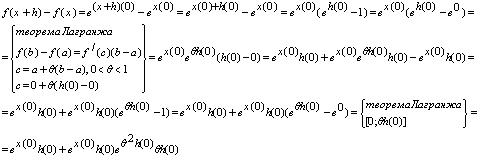
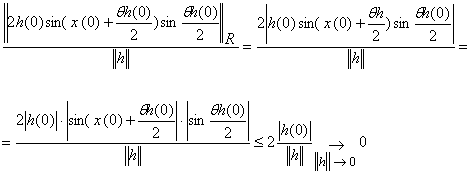
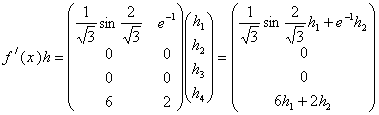



0 комментариев