Навигация
2. Цилиндрические координаты.
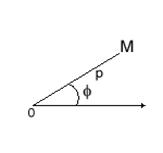
Отнесём область ![]() к системе цилиндрических координат
к системе цилиндрических координат ![]() , в которой положение точки M в пространстве определяется полярными координатами
, в которой положение точки M в пространстве определяется полярными координатами ![]() ее проекции Р на плоскость Oxy и ее аппликатой (z). Выбирая взаимное расположение осей координат, как указано на рис. 5, установим связь, между декартовыми и цилиндрическими координатами точки М, именно:
ее проекции Р на плоскость Oxy и ее аппликатой (z). Выбирая взаимное расположение осей координат, как указано на рис. 5, установим связь, между декартовыми и цилиндрическими координатами точки М, именно:
![]() (*)
(*)
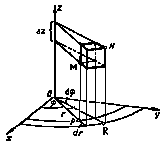
Рис.5
Разобьем область ![]() на частичные области
на частичные области ![]() тремя системами координатных поверхностей:
тремя системами координатных поверхностей: ![]() которыми будут соответственно круговые цилиндрические поверхности, осью которых является ось Оz, полуплоскости, проходящие через ось Оz, и плоскости, параллельные плоскости Оху. Частичными областями
которыми будут соответственно круговые цилиндрические поверхности, осью которых является ось Оz, полуплоскости, проходящие через ось Оz, и плоскости, параллельные плоскости Оху. Частичными областями ![]() служат прямые цилиндры MN (рис. 5). Так как объем цилиндра MN равен площади основания, умноженной на высоту, то для элемента объема получаем выражение
служат прямые цилиндры MN (рис. 5). Так как объем цилиндра MN равен площади основания, умноженной на высоту, то для элемента объема получаем выражение
![]()
Преобразование тройного интеграла ![]() к цилиндрическим координатам производится совершенно аналогично преобразованию двойного интеграла к полярным. Для этого нужно в выражении подынтегральной функции
к цилиндрическим координатам производится совершенно аналогично преобразованию двойного интеграла к полярным. Для этого нужно в выражении подынтегральной функции ![]() переменные x, y, z заменить по формулам (*) и взять элемент объёма равным
переменные x, y, z заменить по формулам (*) и взять элемент объёма равным ![]()
Получим
![]()
Если, в частности, ![]() то интеграл выражает объём V области
то интеграл выражает объём V области ![]()
![]()
Вычисление тройного интеграла в цилиндрических координатах приводится к интегрированиям по r, по ![]() и по z на основании тех же принципов, что и в случае декартовых координат. В частности, если областью интегрирования служит внутренность цилиндра
и по z на основании тех же принципов, что и в случае декартовых координат. В частности, если областью интегрирования служит внутренность цилиндра ![]() то пределы трехкратного интеграла постоянны и не меняются при перемене порядка интегрирования:
то пределы трехкратного интеграла постоянны и не меняются при перемене порядка интегрирования:
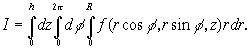
3. Сферические координаты.
Отнесём теперь область интегрирования ![]() к системе сферических координат
к системе сферических координат ![]() . В этой системе координат положение точки M в пространстве определяется её расстоянием r от начала координат (длина радиуса-вектора точки), углом
. В этой системе координат положение точки M в пространстве определяется её расстоянием r от начала координат (длина радиуса-вектора точки), углом ![]() между радиусом-вектором точки и осью Oz и углом
между радиусом-вектором точки и осью Oz и углом ![]() между проекцией радиуса вектора точки на плоскость Oxy и осью Ox (рис. 6). При этом
между проекцией радиуса вектора точки на плоскость Oxy и осью Ox (рис. 6). При этом ![]() может изменятся то 0 до
может изменятся то 0 до![]() а
а ![]() - от 0 до
- от 0 до ![]() .
.
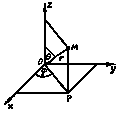
Рис.6
Связь между сферическими и декартовыми координатами легко устанавливается. Из рис.6 имеем
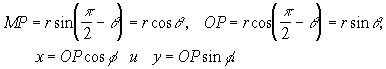
Отсюда
![]() (**)
(**)
Разобьем область ![]() на частичные области
на частичные области ![]() , тремя системами координатных поверхностей:
, тремя системами координатных поверхностей: ![]() которыми будут
которыми будут
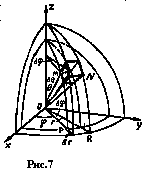
соответственно сферы с центром в начале координат, полуплоскости, проходящие, через ось Оz, и конусы с вершиной в начале координат и с осями, совпадающими с одной из полуосей Оz. Частичными областями ![]() служат “шестигранники” (рис. 7). Отбросив бесконечно малые высших порядков, будем рассматривать шестигранник MN как прямоугольный параллелепипед с измерениями, равными:
служат “шестигранники” (рис. 7). Отбросив бесконечно малые высших порядков, будем рассматривать шестигранник MN как прямоугольный параллелепипед с измерениями, равными: ![]() по направлению полярного радиуса,
по направлению полярного радиуса, ![]() по направлению меридиана,
по направлению меридиана, ![]() по направлению параллели. Для элемента объема мы получим тогда выражение
по направлению параллели. Для элемента объема мы получим тогда выражение
![]()
Заменив в тройном интеграле ![]() по формулам (**) и взяв элемент объема равным полученному выражению, будем иметь
по формулам (**) и взяв элемент объема равным полученному выражению, будем иметь
![]()
Особенно удобно применение сферических координат в случае, когда область интегрирование ![]() - шар с центром в начале координат или шаровое кольцо. Например, в последнем случае, если радиус внутреннего шара
- шар с центром в начале координат или шаровое кольцо. Например, в последнем случае, если радиус внутреннего шара ![]() , а внешнего
, а внешнего ![]() , пределы интегрирования следует расставить так:
, пределы интегрирования следует расставить так:
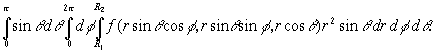
Если ![]() - шар, то нужно положить
- шар, то нужно положить ![]()
A) Пример.
Вычислим объем шара радиуса R. В этом случае подынтегральную функцию надо взять равной 1, и мы получим
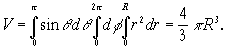
Применение тройных интегралов.
Для вычисления координат центра тяжести тела нужны статические моменты относительно координатных плоскостей Оху, Охz, Оуz; обозначим их соответственно ![]() Повторяя рассуждения получим следующие формулы для координат
Повторяя рассуждения получим следующие формулы для координат ![]() центра тяжести неоднородного тела, плотность которого задается функцией
центра тяжести неоднородного тела, плотность которого задается функцией ![]() занимающего область
занимающего область ![]() :
:
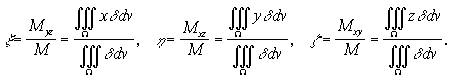
Если тело однородно, т. е. ![]() , то формулы упрощаются:
, то формулы упрощаются:
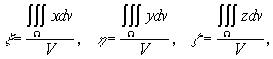
где V- объём тела.
Пример. Найдем центр тяжести однородного полушара ![]() :
:
![]()
Две координаты центра тяжести ![]() равны нулю, ибо полушар симметричен относительно оси Оz (тело вращения с осью Оz).
равны нулю, ибо полушар симметричен относительно оси Оz (тело вращения с осью Оz).
Интеграл ![]() удобно вычислить, перейдя к сферическим координатам:
удобно вычислить, перейдя к сферическим координатам:
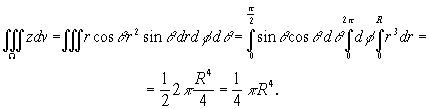
Так как объём полушара равен ![]() то
то
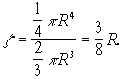
Перейдём к вычислению моментов инерции тела относительно координатных осей. Так как квадраты расстояний от точки P(x, y, z) до осей Ox, Oy, Oz соответственно равны ![]() то полагая для простоты
то полагая для простоты ![]() получим следующие формулы :
получим следующие формулы :
![]()
Аналогично плоскому случаю интегралы
![]()
называются центробежными моментами инерции.
Для полярного момента инерции формула имеет вид
![]()
Если тело неоднородное, то в каждой формуле под знаком интеграла будет находиться дополнительный множитель ![]() - плотность тела в точке P.
- плотность тела в точке P.
Пример. Вычислим полярный момент инерции однородного шара радиуса R. В этом случае очень удобно перейти к сферическим координатам. Будем иметь
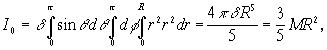
где М—масса шара.
Так как для сферы моменты инерции относительно осей координат, очевидно, равны между собой, то, учитывая, что ![]() получим
получим
![]()
Моменты инерции тела относительно оси играют важную роль при вычислении кинетической энергии тела при его вращении около соответствующей оси. Пусть тело ![]() вращается около оси Оz с постоянной угловой скоростью
вращается около оси Оz с постоянной угловой скоростью ![]() . Найдем кинетическую энергию
. Найдем кинетическую энергию ![]() тела. Как известно, кинетическая энергия точки измеряется величиной
тела. Как известно, кинетическая энергия точки измеряется величиной ![]() , где т - масса точки, а
, где т - масса точки, а ![]() - величина ее скорости. Кинетическая энергия системы точек определяется как сумма кинетических энергий отдельных точек, а кинетическая энергия тела - как сумма кинетических энергий всех частей, на которые оно разбито. Это обстоятельство позволяет применить для вычисления .кинетической энергии интеграл.
- величина ее скорости. Кинетическая энергия системы точек определяется как сумма кинетических энергий отдельных точек, а кинетическая энергия тела - как сумма кинетических энергий всех частей, на которые оно разбито. Это обстоятельство позволяет применить для вычисления .кинетической энергии интеграл.
Возьмем какую-нибудь окрестность ![]() точки Р(х, у, z) тела
точки Р(х, у, z) тела ![]() . Величина линейной скорости
. Величина линейной скорости ![]() точки Р при вращении около оси Оz равна
точки Р при вращении около оси Оz равна ![]() и значит, кинетическая энергия части
и значит, кинетическая энергия части ![]() тела
тела ![]() выразится так :
выразится так :
![]()
где ![]() - плотность тела в точке Р. Для кинетической энергии всего тела
- плотность тела в точке Р. Для кинетической энергии всего тела ![]() получаем
получаем
![]()
т.е.
![]()
Кинетическая энергия тела, вращающегося около некоторой оси с постоянной угловой скоростью, равна половине квадрата угловой скорости, умноженной на момент инерции тела относительно оси вращения.
Список использованной литературы.
1. А.Ф. Бермант ,И.Г. Араманович.
Краткий курс математического анализа для втузов: Учебное пособие для втузов: - М.: Наука, Главная редакция физико-математической литературы, 1971 г.,736с.
Похожие работы
... так: , (10) где F1 и F2 – функции, полученные при подстановке в функцию f вместо x, y, z их выражений через цилиндрические (8) или сферические (9) координаты. 1.4 Геометрические и физические приложения кратных интегралов 1) Площадь плоской области S: (11) Пример 1. Найти площадь фигуры D, ограниченной линиями у = 2, у = 5. Решение. Эту площадь удобно вычислять, считая у ...
... выражения типа дивергенции по п- мерной области и интеграл по ограничивающей ее сверхповерхности S с уравнением L(x,y,z,…)=0. Если придерживаться прежних обозначений, то формула имеет вид (3) Впрочем, Остроградский не применял геометрических образов и терминов, которыми пользуемся мы: геометрия многомерных пространств в то время еще не существовала. В “Мемуаре об исчислении вариаций кратных ...
... и докажите сходимость полученного разложения к порождающей функции. Исследовать на абсолютную и условную сходимость . Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЙ АНАЛИЗ Билет № 12 Сформулируйте теорему Ролля и объясните ее геометрический смысл. Исследуйте функцию на выпуклость и вогнутость. Какая ...
... Из этой теоремы следует, что класс функций, представимых рядами Фурье, довольно широк. Поэтому ряды Фурье нашли широкое применение в различных отделах математики. Особенно успешно ряды Фурье применяются в математической физике и её приложениях к конкретным задачам механики и физики. Этот вопрос можно решить с помощью теоремы Дирихле. («Краткий курс высшей математики», Шнейдер и др., стр. 181) ...
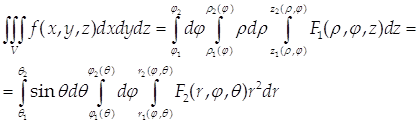
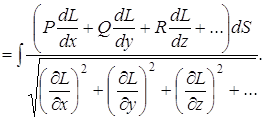

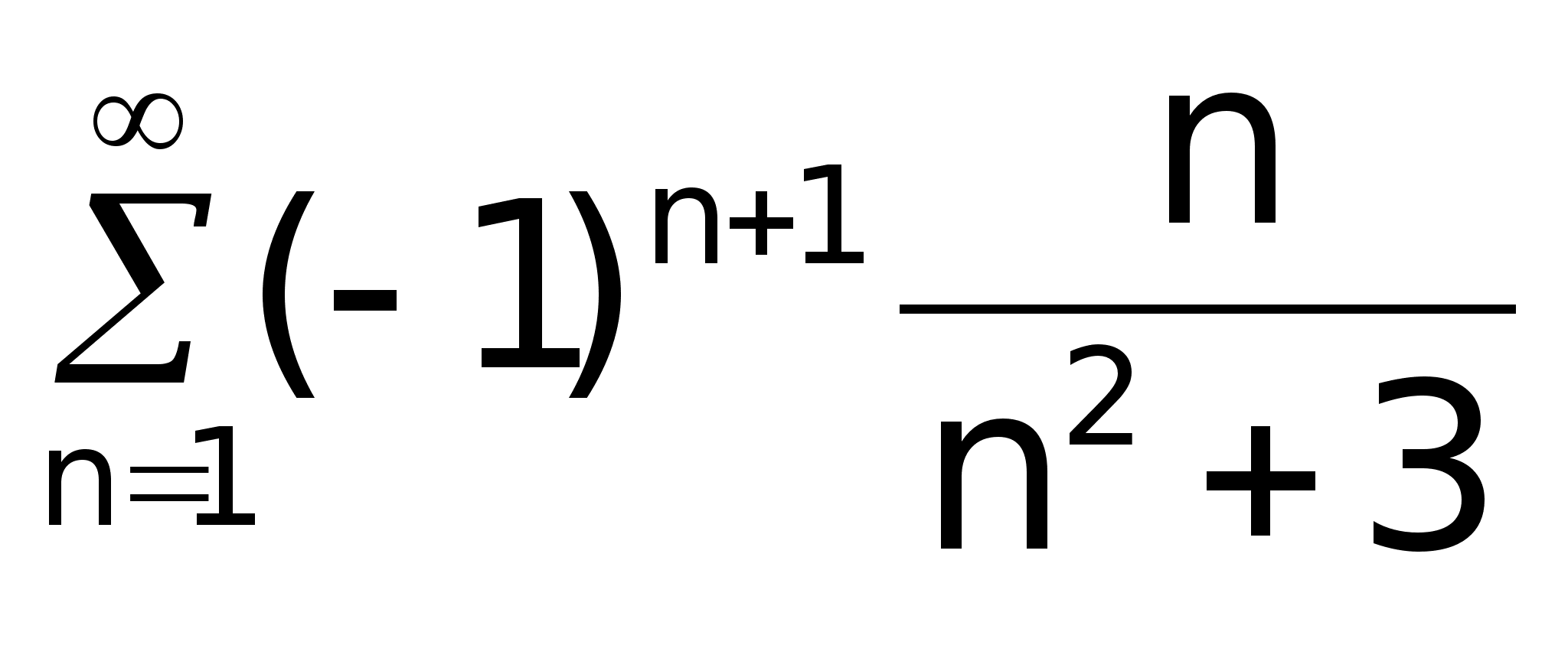
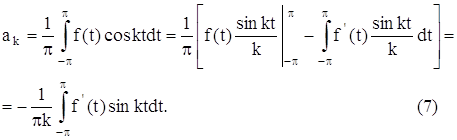
0 комментариев