Навигация
Разработка формальной системы
Кафедра ВПМ
Разработка формальной системы
Пояснительная записка к курсовому проекту
по дисциплине “Математическая логика”
Проверил: Каширин И. Ю.
Рязань 2003г.
Содержание
1. Предметная область.
2. Основные объекты предметной области и отношения на множестве этих объектов.
3. Семантика отношений. Примеры.
4. Свойства отношений.
5. Операции на множестве объектов предметной области. Их семантика. Примеры.
6. Разработка алгебраической системы.
7. Свойства операций.
8. Тип и класс полученной алгебраической системы.
9. Формальная логическая система с аксиоматикой свойств операций. Примеры логического вывода.
10. Программа, демонстрирующая отношения и основные операции алгебраической системы. Пример выполнения программы.
1. Предметная область.
В качестве предметной области будем рассматривать пазл.
2. Основные объекты предметной области и отношения на множестве этих объектов. Примеры.
Основным объектом предметной области является картеж следующего вида:
(а1, а2, а3, а4),
где а1– верхняя сторона пазла;
- а2 - правая сторона пазла;
- а3 - нижняя сторона пазла;
- а4 - левая сторона пазла;
Значения а1, а2, а3, а4 определяются следующим образом (в зависимости от элемента на этой стороне):
- ai = -1 если на стороне вогнутость
- ai = 1 если на стороне выпуклость
- ai = 0 если на стороне нет ни выпуклость ни вогнутости (пустая сторона)
Запись А2 означает, что используется 2я сторона пазла А, т.е. А2 = а2.
![]() Пример 1.
Пример 1.
(-1, 0, 1, 1), т.е.
В качестве отношений возьмем бинарные отношения меньше (<), больше (>) и равенство (=) элементов по:
- количеству выпуклостей (>’; <’; =’)
- количеству вогнутостей (>”; <”; =”)
- по общему числу (=)
3. Семантика отношений.
Введем понятие веса и модуля пазла:
Определение 1. Весом выпуклостей пазла А называется величина Vвп(А), равная количеству сторон при ai= 1, i=![]() .
.
Определение 2. Весом вогнутостей пазла А называется величина Vвг(А), равная количеству сторон при ai= -1, i=![]() .
.
Определение 3. Модулем пазла А называется величина М(А), определяемая следующим уравнением:
М(А)=![]() ,
,
где qi и bi :
![]() ;
; 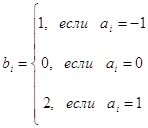 где
где ![]()
Отношение меньше (больше).
Определение 4. Пазл А меньше (больше) пазла В по количеству выпуклостей (по количеству вогнутостей) если вес выпуклостей (вогнутостей) А меньше (больше) веса выпуклостей (вогнутостей) пазла В, т.е.
А <” B (A >” B), если Vвп(A) < Vвп(B) (Vвп(A) > Vвп(B))
[А <’ B (A >’ B), если Vвг(A) < Vвг(B) (Vвг(A) > Vвг(B)) ].
Отношение больше является обратным к отношению меньше, т.е. если A > B, то B < A и наоборот, если A < B, то B > A.
Отношение равенство.
Определение 5. Пазл А равен пазлу В по количеству выпуклостей (вогнутостей), если вес выпуклостей (вогнутости) пазла А равен весу выпуклостей (вогнутости) пазла В, т. е.
- А =’ В по количеству вогнутостей, если Vвг(А)=Vвг(В)
- А =” В по количеству выпуклостей, если Vвп(А)=Vвп(В)
Определение 6. Пазл А равен пазлу В, если равны модули пазлов, т.е A=B, если. М(А)=М(В).
Пример.
А = (-1, 1, 0, 0),
В = (0, 1, 1, -1);
- Vвп(A) =1; Vвп(В)=2; Vвп(A) < Vвп(B), значит A<’B по количеству выпуклостей;
- VМвг(A) =1; Vвг(В)=1; Vвг(A) = Vвг(B), значит A=”B по количеству вогнутостей;
- М(А)=1200; М(В)=221; М(А) ≠ М(В), значит A ≠ B.
4. Свойства отношений.
Отношение больше (меньше)[1].
1) Отношение антирефлексивно.
Доказательство. Отношение А <” A (A >” A) не выполняется ни для какого пазла А, т. к.
Vвг (A) = Vвг (A) и не может быть, что Vвг(A) < Vвг(A) (Vвг(A) > Vвг(A)).
2) Отношение антисимметрично.
Доказательство. Если А <” B (A >” B) то Vвг(A) < Vвг(B) (Vвг(A) > Vвг(B)) => условие Vвг(A) > Vвг(B) (Vвг(A) < Vвг(B)) неверно, отсюда неверно, что А >” B (A <” B).
3) Отношение транзитивно.
Доказательство. Пусть A <” B, B <” C, тогда Vвг(A) < Vвг(B), Vвг(B) < Vвг(C) => Vвг(A) < Vвг(C), т. о. А <” C (Аналогично для отношения больше).
Отношение равенство[2].
1) Отношение рефлексивно.
Доказательство. Для любого пазла А М(A) = М(A) => А = А.
2) Отношение симметрично.
Доказательство. Пусть А = B, тогда М(A) = М(B) => М(B) = М(A) => B = A.
3) Отношение транзитивно.
Доказательство. Пусть А = В, В = С, тогда М(A) = М(B), М(B) = М(C) => М(A) = М(C) => A = C.
Отношение равенства является отношением эквивалентности.
Похожие работы
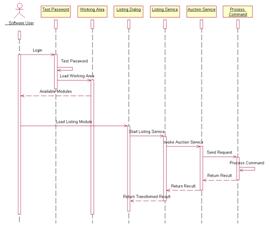
... чем перейти непосредственно к разработке пользовательского интерфейса (ПИ), определим основные требования, предъявляемые к разработке интерфейса пользователя. Разработка пользовательского интерфейса (ПИ) ведется параллельно разработке архитектуры Автоматизированной Системы Управления документооборотом и разработке баз данных в целом и в основном предшествует её имплементации. Процесс разработки ...
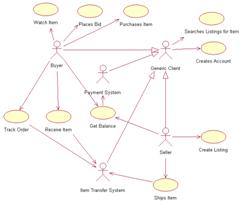
... приведения к базовому узлу, метод удельных весов, метод учета затрат на единицу веса изделия, расчет себестоимости по статьям затрат. В данном проекте приводится расчет себестоимости разработки автоматизированной системы управления торговым предприятием. (АСУТП). АСУТП служит для ведения учета торговой деятельности в Интернет и на аукционе EBay. Из основных преимуществ перед конкурентами стоит ...
... , как класса программного обеспечения и т.д. Проведенный анализ предметной области выявил основные задачи, которые необходимо автоматизировать при разработке информационной системы бюджетного процесса финансового управления Новоегорлыкского сельского поселения. Рассмотрение существующих решений по информатизации управления региональными и местными бюджетами показало, что целесообразно провести ...
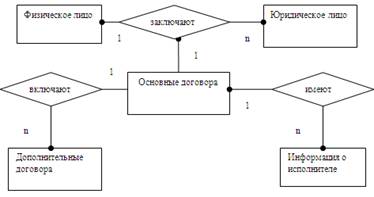
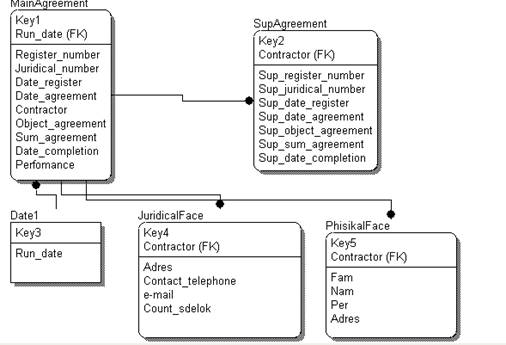
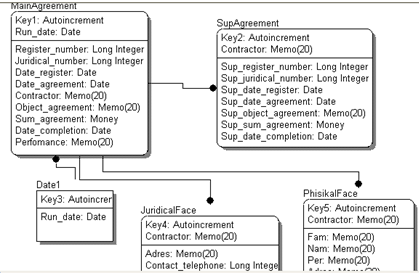
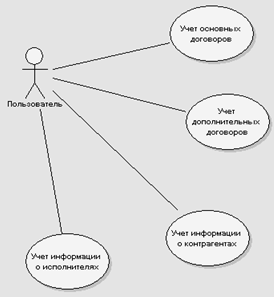
... поступления По требованию начальников Источник Предприятие Список реквизитов дата 3. Проектирование информационного обеспечения 3.1 Описание задачи Необходимо разработать автоматизированную систему для учета договоров. Нужно хранить информацию: Об основных договорах (регистрационный номер, юридический номер, контрагент, дата договора, дата договора, срок окончания, исполнитель, предмет ...





0 комментариев