Навигация
Операции на множестве объектов предметной области. Их семантика
5. Операции на множестве объектов предметной области. Их семантика.
Будем рассматривать две бинарные операции: наложение (+) и склеивание (*); унарная операция: инверсия (()-1) и нульарные: операции слабой (0) и сильной (1) единицы.
Операция слабая единица - 0.
Данная операция - константа 0 представляет - собой картеж вида (0,0,0,0)
Операция сильная единица - 1.
Данная операция - константа 1i - представляет собой один из картежей:
- (1, 0, -1, 0), при i =1;
- (0, 1, 0, -1) , при i =2;
- (-1, 0, 1, 0) , при i =3;
- (0, -1, 0, 1) , при i =4;
где i определяет сторону с элементом «выпуклость».
Операция наложения.
Данная операция накладывает один пазл на другой, в результате чего получается новый пазл. Новый пазл образуется по следующему правилу:
Правило боковых граней:
если на накладываемой стороне 1го пазла находится выпуклость, а у 2го пазла на соответствующей стороне - вогнутость, то результатом будет пустая сторона
если на сторонах обоих пазлов находятся выпуклость (или вогнутость), то в результате получится сторона с выпуклостью (вогнутостью)
если сторона одного из пазлов является пустой, то результирующая сторона будет иметь тот же элемент, что и сторона второго пазла
вышесказанное можно отобразить формулами:
C = A + B:
c’i= ai + bi
ci = 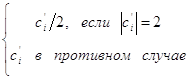
где i = ![]()
Операция наложения справедлива для любых пазлов.
Операция имеет вид:
С = А + В.
Примеры.
1) А = (0, 0, -1, 1),
![]() В = (-1, 1, -1, -1).
В = (-1, 1, -1, -1).
A + B = C = (-1, 1, -1, 0), т.е.
Операция склеивания.
Данная операция склеивает два пазла для получения нового.
Операция выполняется не для всех пазлов, а только для тех, которые удовлетворяют условиям операции:
- склеиваемые стороны на должны бать пустыми и должны иметь противоположные элементы (т.е., например, 1й пазл – вогнутость Þ 2й пазл - выпуклость);
- разность между номерами склеиваемых сторон должна быть по модулю равна 2 (т.е., например, 1й пазл – 2 Þ 2й пазл – 4: |2 - 4| = 2 );
Новый пазл получается следующим образом:
- звездочкой (*) указываются номера склеиваемых сторон;
- элементы сторон, противоположных склеиваемым сторонам, не изменяются;
- элементы двух других сторон образуются по правилу боковых сторон ;
Операция имеет вид: С = А1 * В3 = (а1*, а2, а3, а4) * (b1, b2, b3*, b4)
Пример.
А = (0, 1, -1, 0),
В = (-1, 1, 0, -1).
А2*В4 = (0, 1*, -1, 0) * (-1, 1, 0, -1*) = (-1, 1, -1,0), т.е.
![]()
Операция инверсия.
Данная операция инвертирует пазл, т. е. заменяет выпуклости вогнутостями и наоборот, в результате чего получается новый пазл. Операция имеет вид: С = А-1.
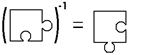 Пример.
Пример.
А = (0, 1, -1, 0)
А-1 = С = (0, -1, 1, 0), т. е.
6. Алгебраическая система.
Определение 7. Система трех множеств Œ = <А, Ω, R> называется алгебраической системой, где А – множество однотипных элементов, называемое носителем алгебры или базовым множеством, Ω – множество операций с областью определения и областью значений в множестве А, R – множество отношений на элементах множества А.
Множество А представляет собой множество всех пазлов, представленных в виде картежей, описанных выше.
Сигнатура алгебры Ω = { + , * , -1() , 0 , 1 }.
R = {<, <’, <”, >, >’, >”, =, =’, =”}
Согласно определению операций, мы получим пазл в виде картежа, описанного выше, значит мы получим элемент базового множества, что говорит о замкнутости операций.
7. Свойства операций.
Свойство единицы:
А + А-1 = А-1 +А = 1 – сильная единица:
Аi * 0 = 0 * Ai = A, i=![]() - слабая единица;
- слабая единица;
Операция наложения.
1) Операция идемпотентна, поскольку для данной операции справедливо утверждение
A + A = A;
2) Операция коммутативна, поскольку для данной операции справедливо утверждение
A + B = B + A;
3) Операция не ассоциативна, поскольку для нее справедливо утверждение
A + (B + C) ¹ (A + B) + C.
Свойства по отношению к операции склеивание:
4) Операция не дистрибутивна слева, т. к. A + (B * C) ≠ (A + B) * (A + C)
5) Операция не дистрибутивна справа, т. к. (A * B) + C ≠ (A + C) * (B + C)
Операция склеивание.
Поскольку условие операции не выполняться для всех пазлов, то операция склеивания:
1) не идемпотентна
2) не коммутативна
3) не ассоциативна
и по отношению к операции наложения:
4) не дистрибутивна слева
5) не дистрибутивна справа
Похожие работы
... чем перейти непосредственно к разработке пользовательского интерфейса (ПИ), определим основные требования, предъявляемые к разработке интерфейса пользователя. Разработка пользовательского интерфейса (ПИ) ведется параллельно разработке архитектуры Автоматизированной Системы Управления документооборотом и разработке баз данных в целом и в основном предшествует её имплементации. Процесс разработки ...
... приведения к базовому узлу, метод удельных весов, метод учета затрат на единицу веса изделия, расчет себестоимости по статьям затрат. В данном проекте приводится расчет себестоимости разработки автоматизированной системы управления торговым предприятием. (АСУТП). АСУТП служит для ведения учета торговой деятельности в Интернет и на аукционе EBay. Из основных преимуществ перед конкурентами стоит ...
... , как класса программного обеспечения и т.д. Проведенный анализ предметной области выявил основные задачи, которые необходимо автоматизировать при разработке информационной системы бюджетного процесса финансового управления Новоегорлыкского сельского поселения. Рассмотрение существующих решений по информатизации управления региональными и местными бюджетами показало, что целесообразно провести ...
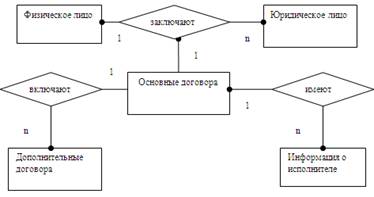
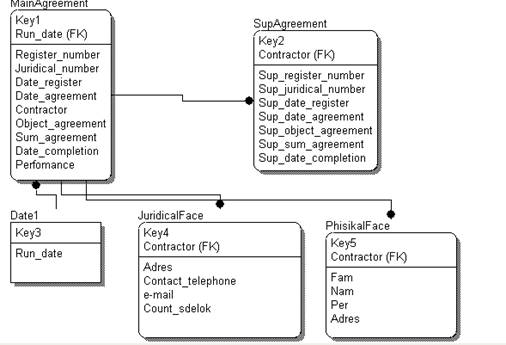
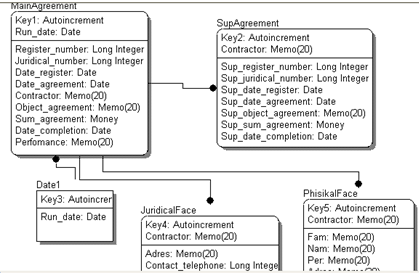
... поступления По требованию начальников Источник Предприятие Список реквизитов дата 3. Проектирование информационного обеспечения 3.1 Описание задачи Необходимо разработать автоматизированную систему для учета договоров. Нужно хранить информацию: Об основных договорах (регистрационный номер, юридический номер, контрагент, дата договора, дата договора, срок окончания, исполнитель, предмет ...





0 комментариев