Навигация
Основные теоремы о линейных оптимальных быстродействиях
12. Основные теоремы о линейных оптимальных быстродействиях.
Т е о р е м а 2.2. Для каждого нетривиального решения y(t) уравнения (2.11) соотношение (2.12) однозначно определяет допустимое управление u(t); при этом оказывается, что функция u(t) кусочно-постоянна и её значениями являются лишь вершины многогранника U.
Каждую точку разрыва оптимального управления мы будем называть точкой переключения.
Т е о р е м а 2.3. Предположим, что многогранник U является r-мерным параллелепипедом (2.2) и что все собственные значения матрицы A=(aij), составленной из коэффициентов уравнений (2.1), действительны. Тогда в оптимальном управлении u(t)=(u1(t),…, ur(t)) каждая из функций ub(t), b=1,…,r, кусочно-постоянна, принимает только значения ab и bb (см. (2.2)) и имеет не более n-1 переключений (т. е. не более n интервалов постоянства), где n — порядок системы (2.1).
Т е о р е м а 2.4 (т е о р е м а е д и н с т в е н н о с т и). Пусть u1(t) и u2(t) — два оптимальных управления, заданных соответственно на отрезках t0£t£t1 и t0£t£t2 и переводящих точку x0 в начало координат. Тогда эти управления совпадают, т. е. t1=t2 и u1(t)ºu2(t) на отрезке t0£t£t1.
Областью управляемости для объекта (2.5) мы будем называть множество всех точек x0 фазового пространства X, из которых возможно при помощи какого-либо допустимого управления попасть в начало координат. Само начало координат мы также будем причислять к области управляемости. Ясно, что вопрос о нахождении оптимальных процессов разумно ставить лишь в случае, если начальное фазовое состояние x0 принадлежит области управляемости (ведь из точек, не принадлежащих области управляемости, вообще нельзя попасть в начало координат).
Т е о р е м а 2.5 (т е о р е м а с у щ е с т в о в а н и я). Область управляемости является выпуклым открытым множеством фазового пространства X; для любой точки x0, принадлежащей области управляемости, существует оптимальное управление, переводящее точку x0 в начало координат.
Т е о р е м а 2.6. Если в линейной задаче оптимального управления матрица A (см. (2.3)) устойчива, т. е. все её собственные значения имеют отрицательные действительные части, то область управляемости совпадает со всем фазовым пространством X. Следовательно, для любой точки x0ÎX существует оптимальное управление, переводящее фазовую точку x0 в начало координат.
§ 5. Решение задачи синтеза для линейных задач второго порядка
13. Упрощение уравнений линейного управляемого объекта. Нередко бывает, что в линейной задаче общая запись уравнений движения объекта в виде (2.1) неудобна и целесообразно воспользоваться некоторыми упрощениями. Мы здесь отметим стандартные упрощения, которые можно осуществить с помощью замены координат.
q Прежде всего, рассмотрим вопрос о замене координат в фазовом пространстве X рассматриваемого управляемого объекта. Предположим, что в пространстве X вместо координат x1,…, xn введены новые координаты y1,…, yn, связанные с прежними координатами соотношениями
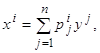
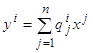 (2.13)
(2.13)
(где матрицы P=(pij) и Q=(qij) взаимно обратны). Ясно, что при такой замене линейная система (2.1) превращается в новую линейную систему
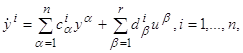
коэффициенты которой легко вычисляются:
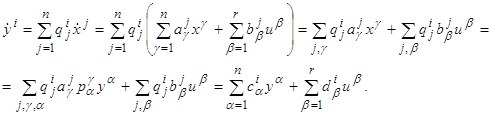
Таким образом, ![]() ,
, ![]()
Переходя к векторным обозначениям, можно сказать, что указанная замена координат переводит уравнение (2.5) в уравнение ![]() где матрицы C и D выражаются через матрицы A, B, P, Q по формулам C=QAP, D=QB.
где матрицы C и D выражаются через матрицы A, B, P, Q по формулам C=QAP, D=QB.
Очевидно, при такой замене условия 1), 2), указанные на стр. 15, сохраняются и для уравнения
![]() получаемого после замены. Далее, каждый процесс (u(t), x(t)), удовлетворяющий уравнению
получаемого после замены. Далее, каждый процесс (u(t), x(t)), удовлетворяющий уравнению ![]() переходит в процесс (u(t), y(t)), удовлетворяющий уравнению
переходит в процесс (u(t), y(t)), удовлетворяющий уравнению ![]() (и обратно). Так как при этом время t не меняется, то указанная замена переводит оптимальные процессы для уравнения
(и обратно). Так как при этом время t не меняется, то указанная замена переводит оптимальные процессы для уравнения ![]() (и наоборот). В частности, синтез оптимальных управлений для уравнения
(и наоборот). В частности, синтез оптимальных управлений для уравнения ![]() переводится с помощью преобразования координат (2.13) в синтез оптимальных управлений для уравнения
переводится с помощью преобразования координат (2.13) в синтез оптимальных управлений для уравнения ![]() .
.
Таким образом, если уравнение ![]() окажется проще и для него синтез оптимальных управлений можно будет построить, то из этого синтеза можно (с помощью афинного преобразования (2.13)) получит синтез и для первоначального уравнения
окажется проще и для него синтез оптимальных управлений можно будет построить, то из этого синтеза можно (с помощью афинного преобразования (2.13)) получит синтез и для первоначального уравнения ![]() . В этом и заключается смысл замены координат (2.13): она позволяет заменить матрицу A трансформированной матрицей C=QAP, в то же время вызывая лишь афинное искажение картины синтеза оптимальных управлений. Таким образом, преобразованием (2.13) можно воспользоваться для упрощения матрицы A, составленной из коэффициентов при фазовых координатах.
. В этом и заключается смысл замены координат (2.13): она позволяет заменить матрицу A трансформированной матрицей C=QAP, в то же время вызывая лишь афинное искажение картины синтеза оптимальных управлений. Таким образом, преобразованием (2.13) можно воспользоваться для упрощения матрицы A, составленной из коэффициентов при фазовых координатах.
q Предположим, что в уравнении ![]() матрица A уже приведена к простейшему виду (с помощью описанного выше приёма). Укажем теперь, каким образом может быть упрощена матрица B, составленная из коэффициентов при управляющих параметрах.
матрица A уже приведена к простейшему виду (с помощью описанного выше приёма). Укажем теперь, каким образом может быть упрощена матрица B, составленная из коэффициентов при управляющих параметрах.
С этой целью положим
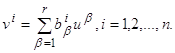 (2.14)
(2.14)
Это означает, что вместо r управляющих параметров u1,…,ur вводятся n других управляющих параметров v1,…, vn, благодаря чему система (2.1) заменяется следующей:
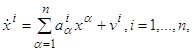
или в векторной форме, ![]()
Нужно только выяснить, в каких пределах может изменяться точка v=(v1, v2,…, vn). Удобно считать, что эта точка v=(v1, v2,…, vn) расположена в том же пространстве X, что и точка x=(x1,…, xn).
Соотношения (2.14) определяют линейное отображение r-мерного пространства переменных u1,…,ur в фазовое пространство X. Образом многогранника U при отображении (2.14) является некоторый выпуклый многогранник в пространстве X, который мы обозначим через V.
Таким образом, получаем два линейных уравнения:
![]() (2.15)
(2.15)
![]() (2.16)
(2.16)
Г л а в а III
СИНТЕЗ ОПТИМАЛЬНЫХ УПРАВЛЕНИЙ ДЛЯ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
§ 6. Решение задачи синтеза в случае комплексных собственных значений
14. Задача синтеза для малых колебаний маятника. Здесь будет дано полное решение задачи синтеза оптимальных управлений для линейных объектов, описываемых уравнениями второго порядка. Фазовое пространство X в этом случае представляет собой плоскость.
Рассмотрим колебание плоского маятника. Как известно колебание маятника, подвешенного к точке опоры, описывается дифференциальным уравнением второго порядка:
![]() (в нашем случае положим β=1)
(в нашем случае положим β=1)
при малых колебаниях маятника Sinφ≈φ тогда уравнение движения маятника запишется в виде:
![]() (3.1)
(3.1)
Управляющий параметр u (скалярный) будем предполагать изменяющимся в пределах -1£u£1.
Пусть ![]() — угол отклонения, а
— угол отклонения, а ![]() — скорость маятника. Тогда уравнение (3.1) перепишется в виде следующей нормальной системы:
— скорость маятника. Тогда уравнение (3.1) перепишется в виде следующей нормальной системы:
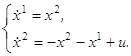 (3.2)
(3.2)
На плоскости x1, x2 «многогранник» U будет представляться отрезком [-1, 1], расположенным на оси x2. Легко видеть, что ось x2 не является собственным инвариантным подпространством матрицы A, которая для системы (3.2) имеет вид:
A=![]() ,
,
и потому условие общности положения всегда выполнено.
Найдём собственные значения матрицы A. Для этого составим характеристическое уравнение |λE─A|=0, т. е. λ2+λ+1=0. Откуда находим, что собственные значения матрицы A такие:
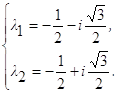
т. е. собственные значения матрицы A комплексные. Введём обозначения ![]() где b≠0.
где b≠0.
Тогда матрица A преобразуется к виду:
![]() =
=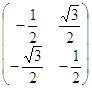 .
.
Будем рассматривать систему, соответствующую матрице ![]() , т. е. систему вида:
, т. е. систему вида:
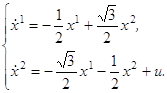 (3.3)
(3.3)
Вначале рассмотрим соответствующую однородную систему:
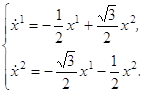 (3.4)
(3.4)
Общее решение этой системы имеет вид:
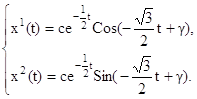
где c, γ – произвольные постоянные интегрирования.
Запишем функцию H и применим принцип максимума.
![]()
где ψ1, ψ2 определяются системой, сопряжённой к системе (3.3), т. е. системой вида:
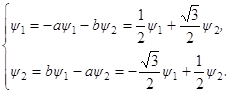 (3.5)
(3.5)
Общее решение этой системы имеет вид:
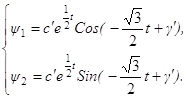
где c’, γ’ – произвольные постоянные интегрирования. Т. е. функция H имеет вид:
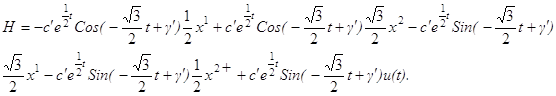
Подставим в функцию H представление решений x1, x2:
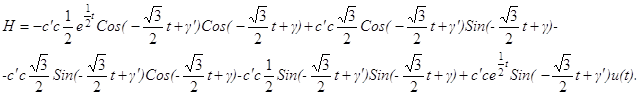
Т. к. собственный вектор матрицы A, соответствующий собственному значению l имеет вид q1─iq2, где q1=(1;─1/2); q2=(0;─![]() ).
).
Пусть q1 и q2 – базисные векторы новой косоугольной системы координат y1, y2. Тогда переход от системы y1, y2 к системе x1, x2 выражается формулами:
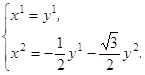
Тогда в новых координатах система уравнений (3.2) запишется в виде
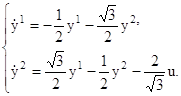
или, иначе, в виде
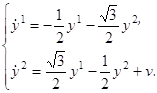
где v=(v1, v2) ─ управляющая точка, которая может меняться в пределах многогранника V, представляющего собой отрезок [![]() ] оси y2.
] оси y2.

![]()
![]()
![]()
![]() Согласно теории вершинам e1=(0,
Согласно теории вершинам e1=(0, ![]() ), e2=(0,
), e2=(0, ![]() ) многогранника V соответствуют точки h1=(1, -
) многогранника V соответствуют точки h1=(1, -![]() ), h2=(-1,
), h2=(-1, ![]() ) (координаты указаны в системе y1, y2), а каждый из углов a1, a2, соответствующих этим вершинам, равен p.
) (координаты указаны в системе y1, y2), а каждый из углов a1, a2, соответствующих этим вершинам, равен p.
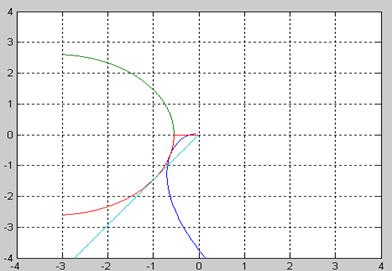
Теперь уже нетрудно построить синтез оптимальных управлений в плоскости y1, y2. Кусками фазовых траекторий будут дуги логарифмических спиралей, т. к. у нас b=1, т. е. b>0 (рис. 18).
При переходе от координат y1, y2 к координатам x1, x2 картина синтеза афинно искажается.
Список используемой литературы: 1. В.Г. Болтянский. «Математические методы оптимального управления», М.: «Наука», 1968г. 2. Л.С. Понтрягин, В.Г. Болтянский, Р.В. Гамкрелидзе, Е.Ф. Мищенко. «Математическая теория оптимальных процессов», 4-е издательство. М.: «Наука», 1983г. 3. Р. Габасов, Ф.М. Кириллова. «Методы оптимизации», Минск, издательство БГУ, 1981г.Похожие работы
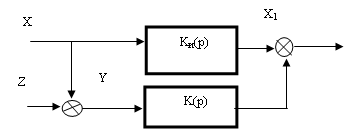
... и В найдем методом неопределенных коэффициентов С учетом полученных выражений При этом передаточная функция представляет аппериодическое звено Где Пример 2. Рассмотрим задачу фильтрации с дифференцированием. Определить оптимальную передаточную функцию - K0 (p) устойчивой и физически реализуемой системы рис.3. Дано: Полезный сигнал - X (t) и помеха - Z (t), представляющие ...
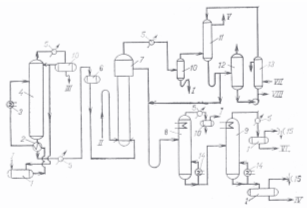
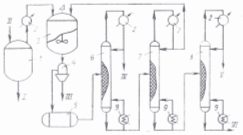
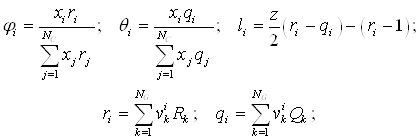
... 8,6961 6,6957 9,9694 - Энергозатраты по схемам ГДЖ/ч 10,0379 15,3918 9,9624 7. Выводы В результате проделанной работы решена задача разделения промышленной смеси продуктов синтеза хлорбензола. В качестве модели наиболее адекватно описывающей парожидкостное равновесие смеси была выбрана модель UNIFAC. Были синтезированы две схемы, состоящие из двух простых двухсекционных колонн ...
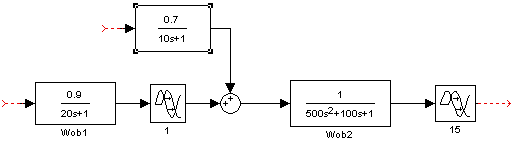
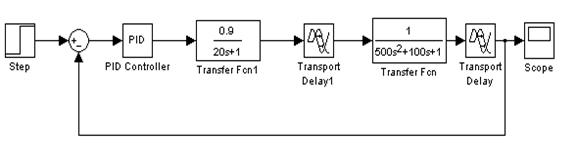
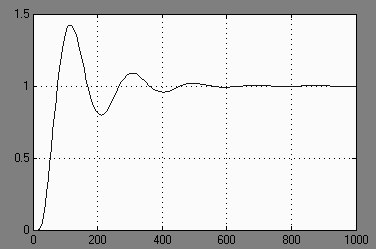
... регулятор на нелинейный элемент. В качестве нелинейного элемента возьмём идеальное реле, статическая характеристика звена изображена на рисунке 23. Рис.23. Идеальное реле Чтобы реализовать данный регулятор в заданной системе автоматического управления, требуется рассчитать значения параметра с. Проанализируем работу системы с нелинейной характеристикой и без неё в Simulink, а затем найдём ...
... эффективностью. Для этого необходимо, прежде всего, выбрать оптимальную технологическую топологию системы, которая определяет характер и порядок соединения отдельных аппаратов в технологической схеме. Очевидно, что с синтезом ХТС тесно связана задача оптимизации, которая сводится к нахождению экстремального значения выбранного критерия эффективности (как правило, экономического) функционирования ...

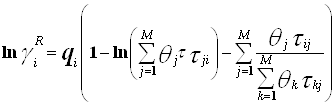



0 комментариев