Навигация
4. Критерий устойчивости Михайлова.
Частотные критерии устойчивости получили наиболее широкое практическое применение, так как, во-первых, они позволяют судить об устойчивости замкнутой системы по более простой передаточной функции системы W ( s ) ; во-вторых, анализ устойчивости можно выполнять и по экспериментально определенным частотным характеристикам; в-третьих, с помощью частотных характеристик можно судить и о качестве переходных процессов в системе.
А.В. Михайлов первым предложил использовать развитые в радиотехнике Найквистом частотные методы для анализа устойчивости линейных систем регулирования. Сформулированным им в 1938 г. критерий устойчивости назвали его именем. Рассмотрим существо этого критерия.
Пусть характеристическое уравнение замкнутой системы имеет вид
D ( l ) = l n + a1 l n-1 + a2 l n-2 + ... + an = 0. (13)
Зная его корни l 1 , l 2 , ... , l n , характеристический многочлен для уравнения (13) запишем в виде
D ( l ) = ( l - l 1 ) ( l - l 2 ) ... ( l - l n ). (14)
![]()
![]()
![]()
![]()
![]()

![]()



![]()
![]()
![]()
Im Im
0 Re 0 Re
а) б)
Рис.12. Векторное изображение сомно-жителей характерис-тического уравнения замкнутой системы на плоскости :
а - для двух корней l и l i ;
б - для четырех корней l 1 , l ‘1 , l 2 , l ‘2
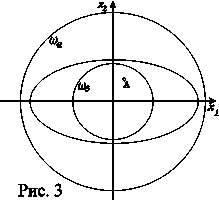
Графически каждый комплексный корень l можно представить точкой на плоскости. Поэтому, в свою очередь, каждый из сомножителей уравнения (14) можно представить в виде разности двух векторов ( l - l i ), как это показано на рис.12,а. Положим теперь, что l = j w ; тогда определяющей является точка w на мнимой оси (рис.12,б). При изменении w от - Ґ до + Ґ векторы j w - l 1 и j w - l ‘1 комплексных корней l и l ‘1 повернуться против часовой стрелки, и приращение их аргумента равно + p , а векторы j w - l 2 и j w - l ‘2 повернутся по часовой стрелке, и приращение их аргумента равно - p . Таким образом, приращение аргумента arg( j w - l i ) для корня характеристического уравнения l i , находящегося в левой полуплоскости, составит + p , а для корня, находящегося в правой полуплоскости, - p . Приращение результирующего аргумента D arg D( j w ) равно сумме приращений аргументов его отдельных сомножителей. Если сре1ди n корней характеристического уравнения m лежит в правой полуплоскости, то приращение аргумента составит
D arg D( j w ) = ( n - m ) p - m p = ( n - 2m ) p . (15)
![]()
![]() - Ґ < w < Ґдля левой для правой
- Ґ < w < Ґдля левой для правой
полуплоскости полуплоскости
Отметим теперь, что действительная часть многочлена
D ( j w ) = ( j w )n + a1 ( j w )n-1 + a2 ( j w )n-2 + ... + an (16)
содержит лишь четные степени w , а мнимая его часть - только нечетные, поэтому
arg D ( j w ) = - arg D ( -j w ), (17)
и можно рассматривать изменение частоты только на интервале w от 0 до Ґ . В этом случае приращение аргумента годографа характеристического многочлена
D arg D( j w ) = ( n - 2m ) p / 2 . (18)
0 Јw < Ґ
Если система устойчива, то параметр m = 0, и из условия (18) следует, что приращение аргумента
D arg D( j w ) = n p / 2 . (19)
0 Јw < Ґ
На основании полученного выражения сформулируем частотный критерий устойчивости Михайлова: для того чтобы замкнутая система автоматического регулирования была устойчива, необходимо и достаточно, чтобы годограф характеристического многочлена в замкнутой системе (годограф Михайлова) начинался на положительной части действительной оси и проходил последовательно в положительном направлении, не попадая в начало координат, n квадрантов комплексной плоскости ( здесь n - порядок характеристического уравнения системы).
![]()
![]()
![]()
![]()
j V’ j V’
Похожие работы
... строки. Очевидно, что такая операция не изменит знака членов следующей строки и не отразится на конечном результате. Например, элементы третьей строки таблицы (45) можно было бы разделить на 8 для упрощения последующих вычислений. Анализ результатов устойчивости в нелинейных системах. При исследовании устойчивости в цепях постоянного тока при малых возмущениях обнаружение неустойчивости ...
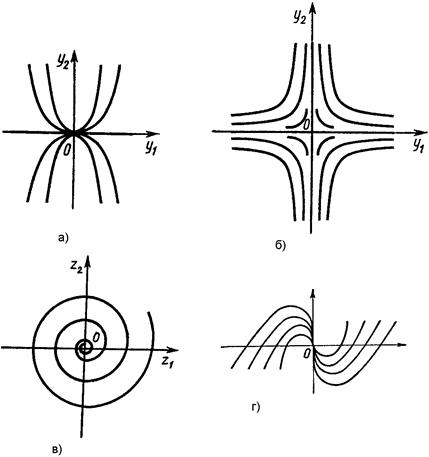
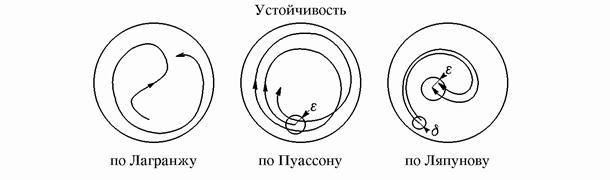
... начальным условиям . Пусть — характеристическое уравнение для определения мультипликаторов. Так как , то оно принимает вид , где . 2. Устойчивость решений систем дифференциальных уравнений. 2.1. Устойчивость по Ляпунову. Вводя определение устойчивости по Лагранжу и Пуассону в пункте 1.3, описывались свойства одной отдельно взятой траектории. Понятие устойчивости по Ляпунову характеризует ...
... владеет Украина, является одним из важнейших измерений ее миссии. То, что она призвана дать мировому сообществу будущего, с точки зрения общечеловеческого развития, становится глобальной миссией Украины. Интерпретация устойчивого развития по М. Руденко позволяет определять наиболее ценные из интеллектуальных достижений, которые должны передаваться потомкам, и формулировать требования к ним. Так, ...
... были определены для всех подставляемых в них значений аргументов. Таким образом, точка с координатами должна принадлежать множеству для всех значений на интервале . Устойчивость по Ляпунову Рассмотрим систему дифференциальных уравнений (??) Выделим некоторое решение системы (??) и назовем его невозмущенным решением. Решение назовем устойчивым в смысле Ляпунова ...
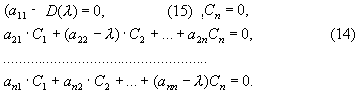
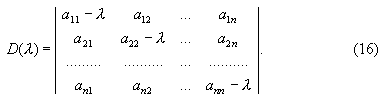
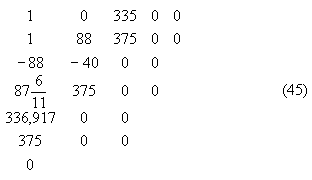
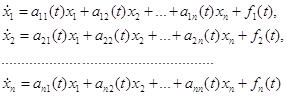
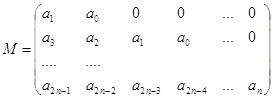
0 комментариев