Навигация
3. Постановка задачи
3.1. Описание модели. В настоящее время наблюдается значительно возрастающий интерес к исследованию нелинейных волновых процессов в различных областях физики (например, в оптике, физике плазмы, радиофизике, гидродинамике и т.д.). Для изучения волн малой, но конечной амплитуды в дисперсионных средах в качестве модельного уравнения часто используют уравнение Кортевега-де Фриза (КдФ):
ut + иих + bиххх = 0 (3.1)
Уравнение КдФ было использовано для описания магнитозвуковых волн, распространяющихся строго поперек магнитного поля или под углами, близкими к ![]() .
.
Основные предположения, которые делаются при выводе уравнения: 1) малая, но конечная амплитуда, 2) длина волны велика по сравнению с длиной дисперсии.
Компенсируя действие нелинейности, дисперсия дает возможность формироваться в дисперсионной среде стационарным волнам конечной амплитуды - уединенным и периодическим. Уединенные волны для уравнения КдФ после работы [8] стали называться солитонами [9]. Периодические волны носят название кноидальных волн. Соответствующие формулы для их описания даны в [4].
3.2. Постановка дифференциальной задачи. В работе исследуется численное решение задачи Коши для уравнения Кортевега-де Фриза с периодическими условиями по пространству в прямоугольнике QT={(t,x):0<t<T, x Î [0,l].
ut + иих + bиххх = 0 (3.2)
u(x,t)|x=0=u(x,t)|x=l (3.3)
с начальным условием
u(x,t)|t=0=u0(x) (3.4)
4. Свойства уравнения Кортевега - де Фриза
4.1. Краткий обзор результатов по уравнению КдФ. Задача Коши для уравнения КдФ при различных предположениях относительно u0(х) рассматривалась во многих работах [10-17]. Задача о существовании и единственности решения с условиями периодичности в качестве краевых условий была решена в работе [10] с помощью метода конечных разностей. Позже, при менее сильных предположениях, существование и единственность были доказана в статье [11] в пространстве L¥(0,T,Hs(R1)), где s>3/2, а в случае периодической задачи - в пространстве L¥(0,T,H¥(C))где С - окружность длины, равной периоду, на русском языке эти результаты представлены в книге [12].
Случай, когда не предполагается какая-либо гладкость начальной функции u0ÎL2(R1), рассмотрен в работе [13]. Там вводится понятие обобщенного решения задачи (3.2),(3.4), устанавливается существование обобщенного решения и(t,х) Î L¥(0,T,L2(R1)) в случае произвольной начальной функции u0 ÎL2(R1); при этом и(t,х) Î L2(0,Т;H-1(-r,r)) для любого r>0, и если для некоторого a > 0 (xau02(x)) Î L1(0,+¥) , то
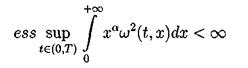 (4.1)
(4.1)
Используя обращение линейной части уравнения при помощи фундаментального решения G(t,x) соответствующего линейного оператора ![]() , вводится класс корректности задачи (3.2),(1.4) и устанавливаются теоремы единственности и непрерывной зависимости решений этой задачи от начальных данных. Также исследуются вопросы регулярности обобщенных решений. Одним из основных результатов является достаточное условие существования непрерывной по Гельдеру при t > 0 производной
, вводится класс корректности задачи (3.2),(1.4) и устанавливаются теоремы единственности и непрерывной зависимости решений этой задачи от начальных данных. Также исследуются вопросы регулярности обобщенных решений. Одним из основных результатов является достаточное условие существования непрерывной по Гельдеру при t > 0 производной ![]() в терминах существования моментов для начальной функции, для любых k и l.
в терминах существования моментов для начальной функции, для любых k и l.
Задача Коши для уравнения КдФ исследовалась также методом обратной задачи рассеяния, предложенном в работе [14]. При помощи этого метода были получены результаты о существовании и гладкости решений при достаточно быстро убывающих начальных функциях, причем в [15] установлен, в частности, результат о разрешимости задачи (3.2),(3.4) в пространстве C¥(О, Т; S(R1)).
Наиболее полный обзор современных результатов по уравнению КдФ можно найти в [16].
4.2. Законы сохранения для уравнения КдФ. Как известно, для уравнения КдФ существует бесконечное число законов сохранения. В работе [17] приводится строгое доказательство этого факта. В работах [11], [12] различные законы сохранения применялись для доказательства нелокальных теорем существования решения задачи (3.2),(3.4) из соответствующих пространств.
Продемонстрируем вывод первых трех законов сохранения для задачи Коши на R1 и периодической задачи.
Для получения первого закона сохранения достаточно проинтегрировать уравнения (3.2) по пространственной переменной. Получим:
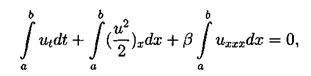
|
|
| отсюда и следует первый закон сохранения: |
Здесь в качестве a и b выступают +¥ и -¥ для задачи Коши и границы основного периода для периодической задачи. Поэтому второе и третье слагаемые обращаются в 0.
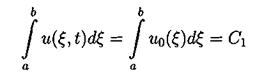 (4.2)
(4.2)
Для вывода второго закона сохранения следует умножить уравнение (3.2) на 2 u(t,x) и проинтегрировать по пространственной переменной. Тогда, используя формулу интегрирования по частям получим:
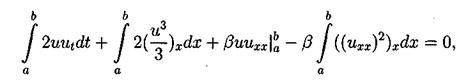
но в силу "краевых" условий все слагаемые кроме первого опять сокращаются
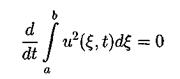
Таким образом второй интегральный закон сохранения имеет вид:
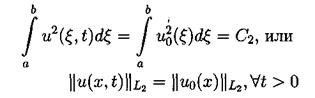 (4.3)
(4.3)
Для вывода третьего закона сохранения нужно умножить наше уравнение (3.2) на (и2 + 2b ихх), таким образом получим:
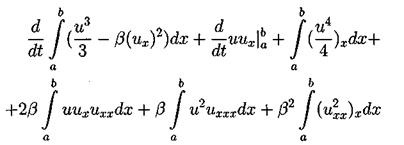
После применения несколько раз интегрирования по частям третий и четвертый интегралы сокращаются. Второе и третье слагаемые исчезают из-за граничных условий. Таким образом из первого интеграла получаем:
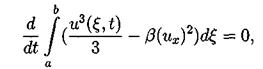
что эквивалентно
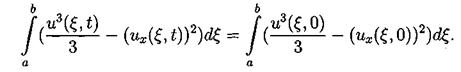 (4.4)
(4.4)
А это и есть третий закон сохранения для уравнения (3.2). Под физическим смыслом первых двух интегральных законов сохранения в некоторых моделях можно понимать законы сохранения импульса и энергии, для третьего и последующих законов сохранения физический смысл охарактеризовать уже труднее, но с точки зрения математики эти законы дают дополнительную информацию о решении, которая используется потом для доказательств теорем существования и единственности решения, исследования его свойств и вывода априорных оценок.
0 комментариев