Навигация
Неявные разностные схемы (обзор). В этом параграфе мы рассмотрим неявные разностные схемы для уравнения Кортевега-де Фриза
39677
знаков
8
таблиц
6
изображений
5.3. Неявные разностные схемы (обзор). В этом параграфе мы рассмотрим неявные разностные схемы для уравнения Кортевега-де Фриза.
Вариант двухслойной схемы - неявная абсолютно устойчивая схема с порядком аппроксимации О (t2, h4) [21]:
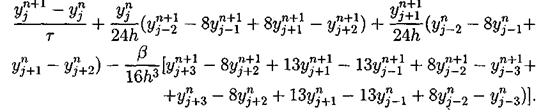
Решение разностной схемы (3.29) вычисляется с помощью семи диагональной циклической прогонки [22]. Вопрос о консервативности этой схемы не исследовался.
В работе [15] предлагается неявная трехслойная схема с весами:
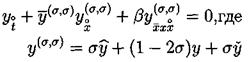(5.10)
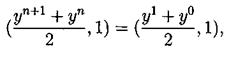
Разностная схемы (5.10) с периодическими по пространству решениями, консервативна, L2-консервативна при s =1/2 и s =1/4 для ее решения имеют место сеточные аналоги интегральных законов сохранения.
6. Численное решение
Численное решение для (3.2), (3.3), (3.4) было проделано с использованием явной схемы
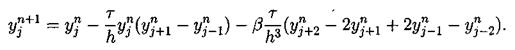(5.7)
Решалась начально-краевая задача на отрезке [0, 2p]. В качестве начальных условий бралась функция
u0(x)=sin (x).
Явным образом было получено решение.
Программа для расчетов была написана на языке Turbo Pascal 7.0. Текст основных частей программы прилагается.
Расчеты велись на вычислительной машине с процессором AMD-K6-2 300 МГц с технологией 3DNOW!, размер оперативной памяти 32 Мб.
7. Заключение
Настоящая работа посвящена исследованию уравнения Кортевега – де Фриза. Проведен обширный литературный обзор по теме исследования. Изучены различные разностные схемы для уравнения КдФ. Выполнен практический счет с использованием явной пяти точечной разносной схемы
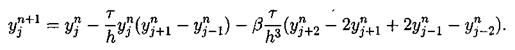
Как показал анализ литературных источников, явные схемы для решения уравнений типа КдФ наиболее применимы. В данной работе также решение было получено с использованием явной схемой.
8. Литература
1. Ландсберг Г.С. Элементарный учебник физики. М.: Наука, 1964. Т. 3.
2. Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. М.: Мир, 1965. Вып.4.
3. Филиппов А. Г Многоликий солитон. М.: Наука, 1986. (Б-чка "Квант"; Вып. 48).
4. Рубанков В.Н. Солитоны, новое в жизни, науке, технике. М.: Знание, 1983. (Физика; Вып. 12).
5. Korteweg D.J., de Vries G. On the change form of long waves advancing in a rectangular channel and on new type of long stationary waves.//Phyl.May. 1895. e5. P. 422-443.
6. Сагдеев Р.З. Коллективные процессы и ударные волны в разреженной плазме.-В кн.: Вопросы теории плазмы, Вып.4. М.: Атомиз-дат, 1964, с.20-80.
7. Березин Ю.А., Карпман В.И. К теории нестационарных волн конечной амплитуды в разреженной плазме. // ЖЭТФ, 1964, т.46, вып.5, с. 1880-1890.
8. Zabusky N.J., Kruskal M.D. Interactions of "solitons"in a collisionless plasma and the reccurence of initial states // Phys.Rev.Lett. 1965. V.15. еб. Р.240-243.
9. Буллаф Р., Кодри Ф. Солитоны. М.: Мир; 1983
10. Sjoberg A. On the Korteweg-de Vries equation, existence and uniqueness, Uppsala University, Department of Computers, 1967
11. Temam R. Sur un probleme non lineare // J.Math.Pures Anal. 1969, V.48, 2, P. 159-172.
12. Лионе Ж.-Л. Некоторые методы решения нелинейных краевых задач. М.: Мир, 1972.
13. Кружков С.Н. Фаминский А.В. Обобщенные решения для уравнения Кортевега-де Фриза.// Матем. сборник, 1983, т. 120(162), еЗ, с.396-445
14.. Gardner C.S., Green J.M., Kruskal M.D., Miura R.M. Method for solving the Korteweg-de Vries equation // Phys.Rev.Lett. 1967. V. 19. P. 1095-1097.
15. Шабат А.Б. Об уравнении Кортевега-де Фриза // ДАН СССР, 1973, т.211, еб, с.1310-1313.
16. Фаминский А.В. Граничные задачи для уравнения Кортевега-де Фриза и его обобщений: Дисс.... докт. физ.-матем. наук,М:РУДН,2001
17. Miura R.M., Gardner C.S., Kruscal M.D. Korteweg-de Vries equation and generlization. II. Existence of conservation laws and constants of motion. // J.Math.Phys. 1968. V.9. P. 1204-1209.
18. Амосов А.А., Злотник А.А. Разностная схема для уравнений движений газа.
19. Самарский А.А., Мажукин В.И., Матус П.П., Михайлик И.А. Z/2-консервативные схемы для уравнения Кортевега-де Фриса.// ДАН, 1997, т.357, е4, с.458-461
20. Березин Ю.А. Моделирование нелинейных волновых процессов. Новосибирск: Наука. 1982.
21. Березин Ю.А., О численных решениях уравнения Кортевега-де Вриза.// Численные методы механики сплошной среды. Новосибирск, 1973, т.4, е2, с.20-31
22. Самарский А.А., Николаев Методы решения сеточных уравнений. М: Наука, 1978
23. Самарский А.А., Гулин А.В. Численные методы. М: Наука, 1989
24. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. М: Наука, 1987
0 комментариев