Оценка
погрешности
при замене
действительного
числа его подходящей
дробью
Теорема
Дирихле
Сократить
дробь
Преобразуйте
в обыкновенную
дробь следующие
цепные дроби:
a) (2, 1, 1, 2, 1, 6, 2, 5); b) (2, 3, 1, 6, 4); c) (1, 3, 2, 4, 3,
1, 1, 1, 5);
Разложите
число 150 на два
положительных
слагаемых, одно
из которых
кратно 11, а второе
– 17
Навигация
Преобразуйте в обыкновенную дробь следующие цепные дроби: a) (2, 1, 1, 2, 1, 6, 2, 5); b) (2, 3, 1, 6, 4); c) (1, 3, 2, 4, 3, 1, 1, 1, 5);
Цепные дроби
53043
знака
21
таблица
1149
изображений
5. Преобразуйте в обыкновенную дробь следующие цепные дроби: a) (2, 1, 1, 2, 1, 6, 2, 5); b) (2, 3, 1, 6, 4); c) (1, 3, 2, 4, 3, 1, 1, 1, 5);
d) (0, 3, 1, 2, 7).
Решение:
a) (2, 1, 1, 2, 1, 6, 2, 5)=
Составим таблицу подходящих дробей:
| 2 | 1 | 1 | 2 | 1 | 6 | 2 | 5 | |
|
| 2 | 3 | 5 | 13 | 18 | 121 | 260 | 1421 |
|
| 1 | 1 | 2 | 5 | 7 | 47 | 101 | 552 |
Ответ: =
b)
(2, 3, 1, 6, 4)=
| 2 | 3 | 1 | 6 | 4 | |
|
| 2 | 7 | 9 | 61 | 253 |
|
| 1 | 3 | 4 | 27 | 112 |
Ответ: =
c) (1, 3, 2, 4, 3, 1, 1, 1, 5)
| 1 | 3 | 2 | 4 | 3 | 1 | 1 | 1 | 5 | |
|
| 1 | 4 | 9 | 40 | 129 | 169 | 298 | 467 | 2633 |
|
| 1 | 3 | 7 | 31 | 100 | 131 | 231 | 362 | 2041 |
Ответ:
=
d)
(0, 3, 1, 2, 7)=
| 0 | 3 | 1 | 2 | 7 | |
|
| 0 | 1 | 1 | 3 | 22 |
|
| 1 | 3 | 4 | 11 | 81 |
Ответ:
=
6. Разложить в цепную дробь и заменить подходящей дробью с точностью до 0,001 следующие числа:
a) 
;
b) 
;
c) 
;
d) 
.
Решение:
a) =.
Выделим
из
его целую часть:
,
а дробную часть -2,
которая 
,
где 
.
Повторяя эту
операцию выделения
целой части
и переворачивания
дробной, получаем:
;
;
.
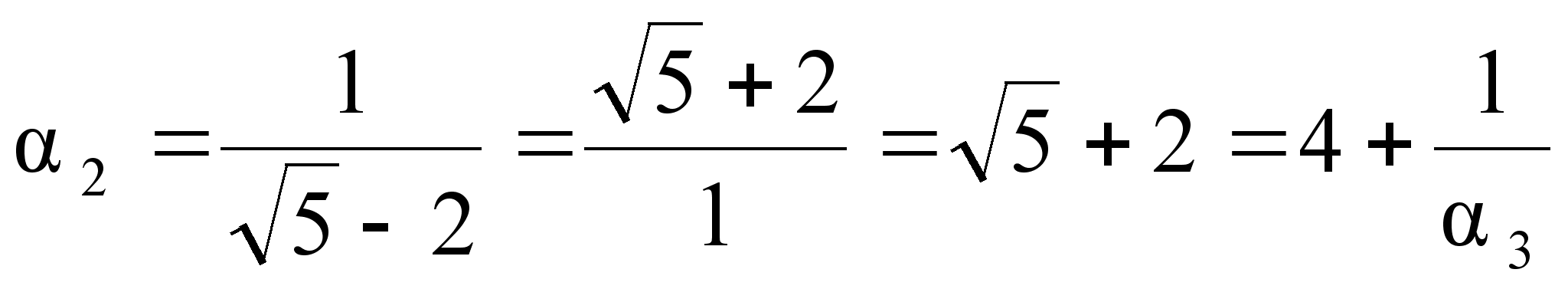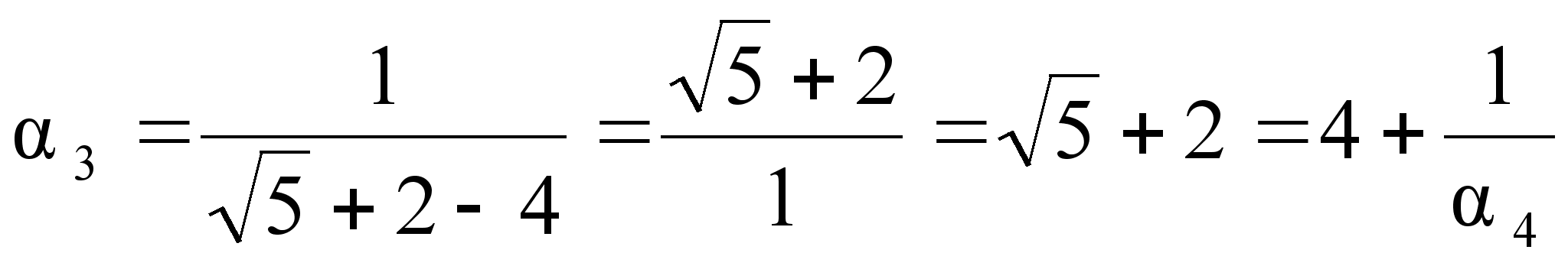Мы
получили, что
,
следовательно,
неполные частные,
начиная с
будут повторяться
и =(2,
(4)).
Составим таблицу подходящих дробей:
| 2 | 4 | 4 | 4 | … | |
|
| 2 | 9 | 38 | ||
|
| 1 | 4 | 17 | 72 |
Нам
необходимо
найти такую
подходящую
дробь 
,
чтобы 
.
Очевидно, что
это 
,
так как 17·72>1000.
Ответ:
.
b)
=;
=5
;
;
;
;
;
.
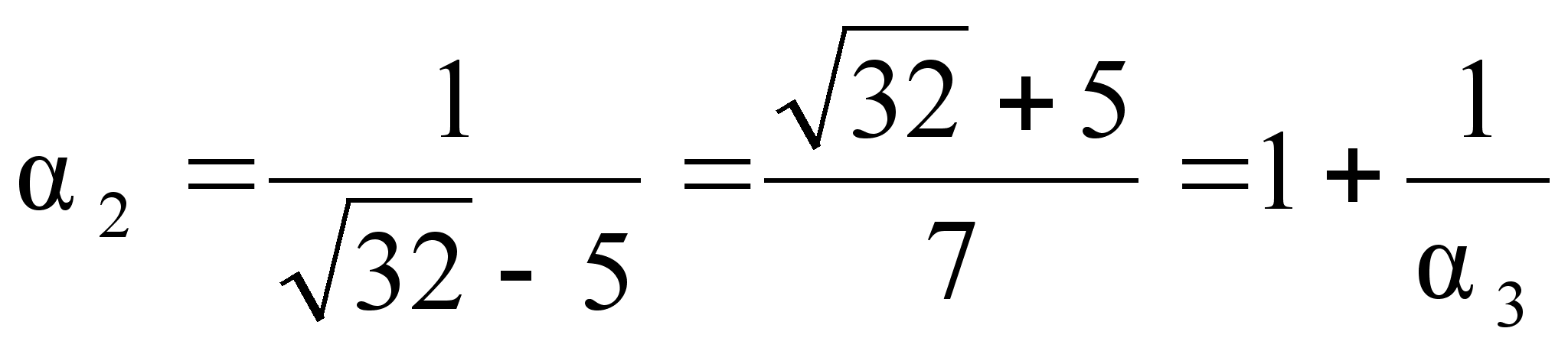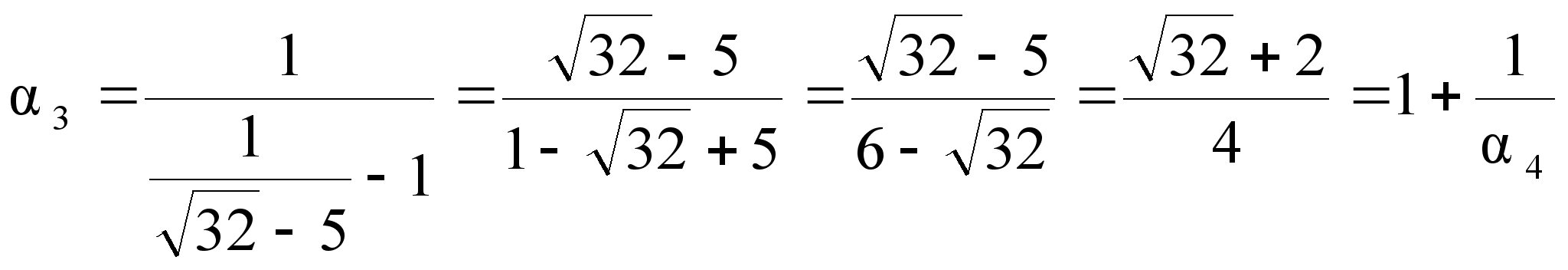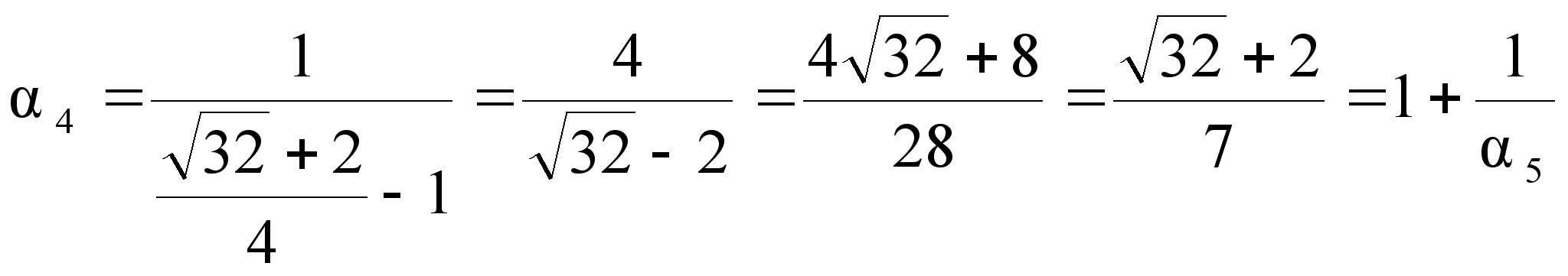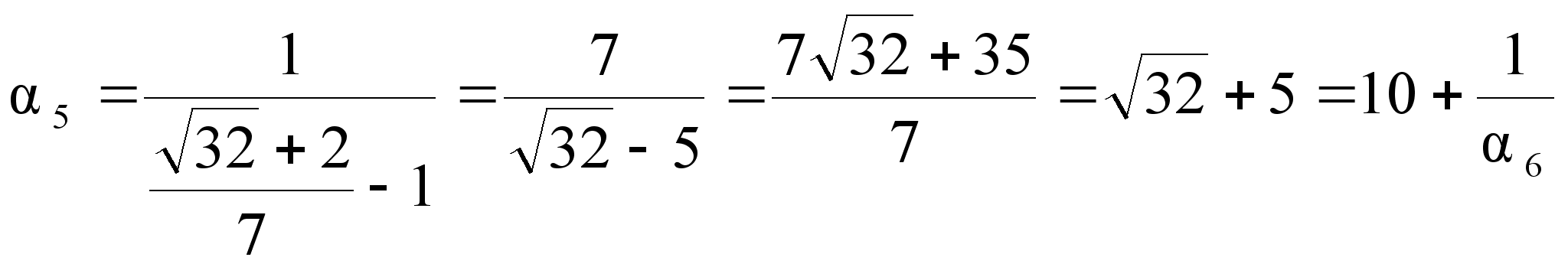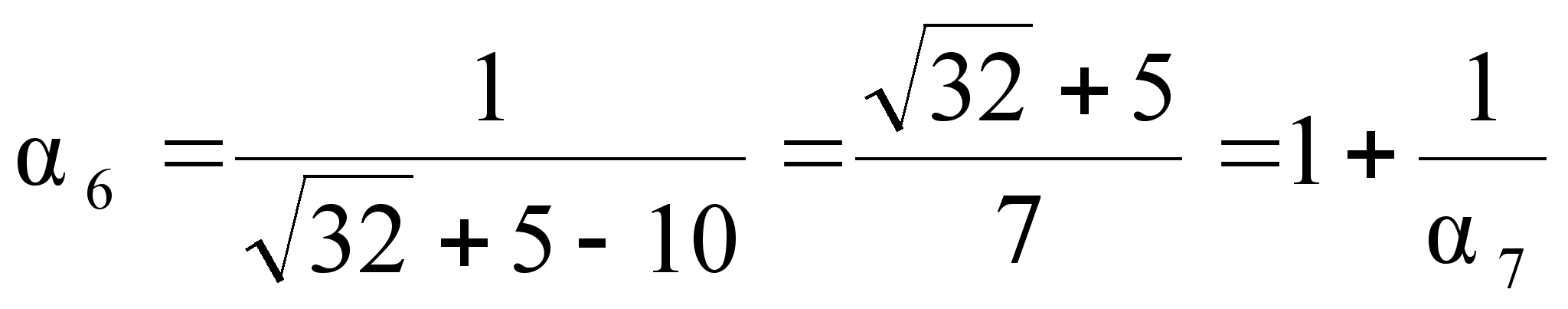Мы
получили 
неполные
частные, начиная
с
будут повторяться
и =(5,
(1, 1, 1, 10)).
| 5 | 1 | 1 | 1 | 10 | 1 | … | |
|
| 5 | 6 | 11 | 17 | 181 | 198 | |
|
| 1 | 1 | 2 | 3 | 32 | 35 |
,
так как 32·35>1000.
Ответ: .
c)
=(3,
2, 5, 2, 7, 2);
| 3 | 2 | 5 | 2 | 7 | 2 | |
|
| 3 | 7 | 38 | 83 | 619 | 1321 |
|
| 1 | 2 | 11 | 24 | 179 | 382 |
,
так как 24·179>1000.
Ответ:
.
d)
=;
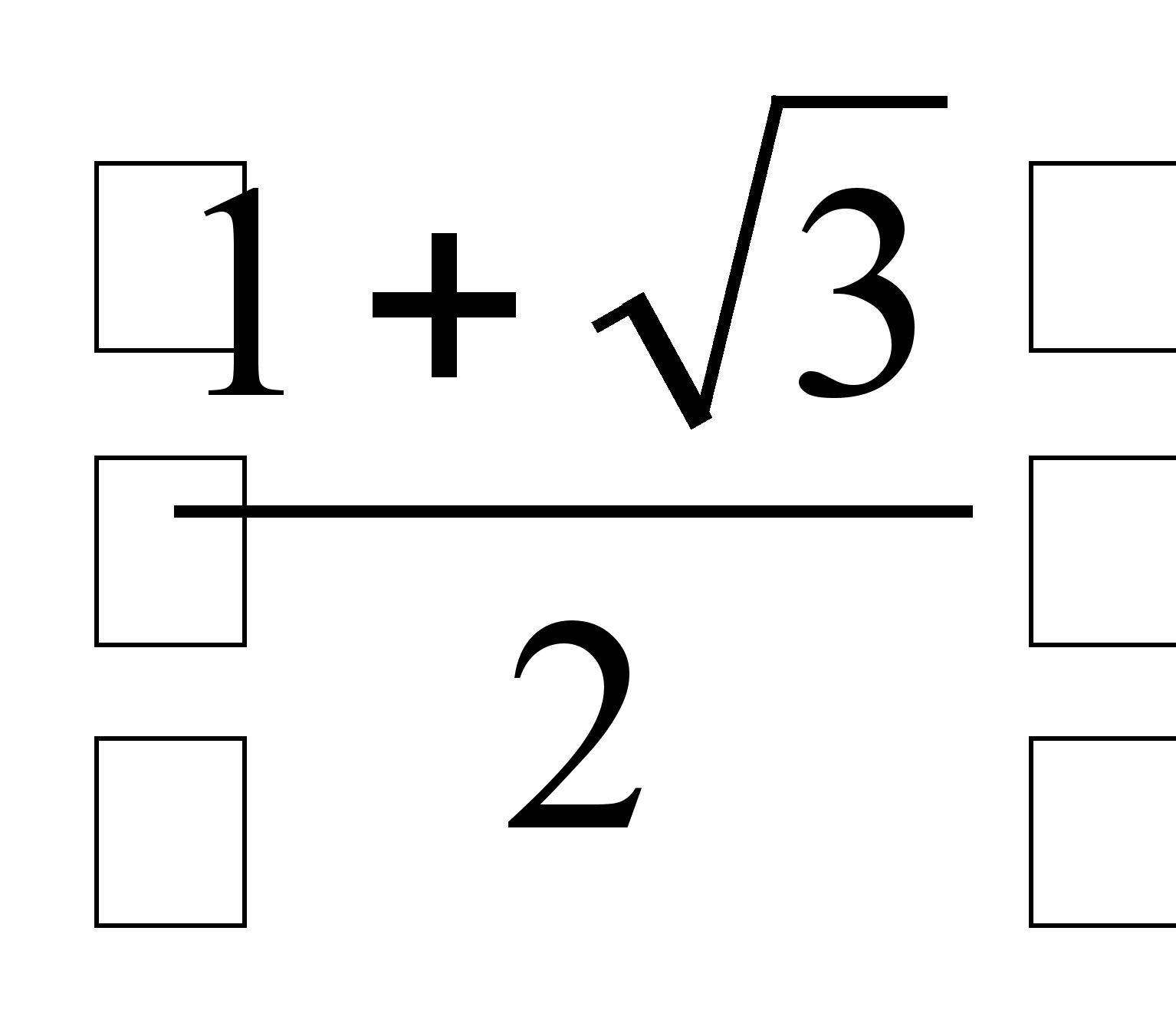=1
;
;
;
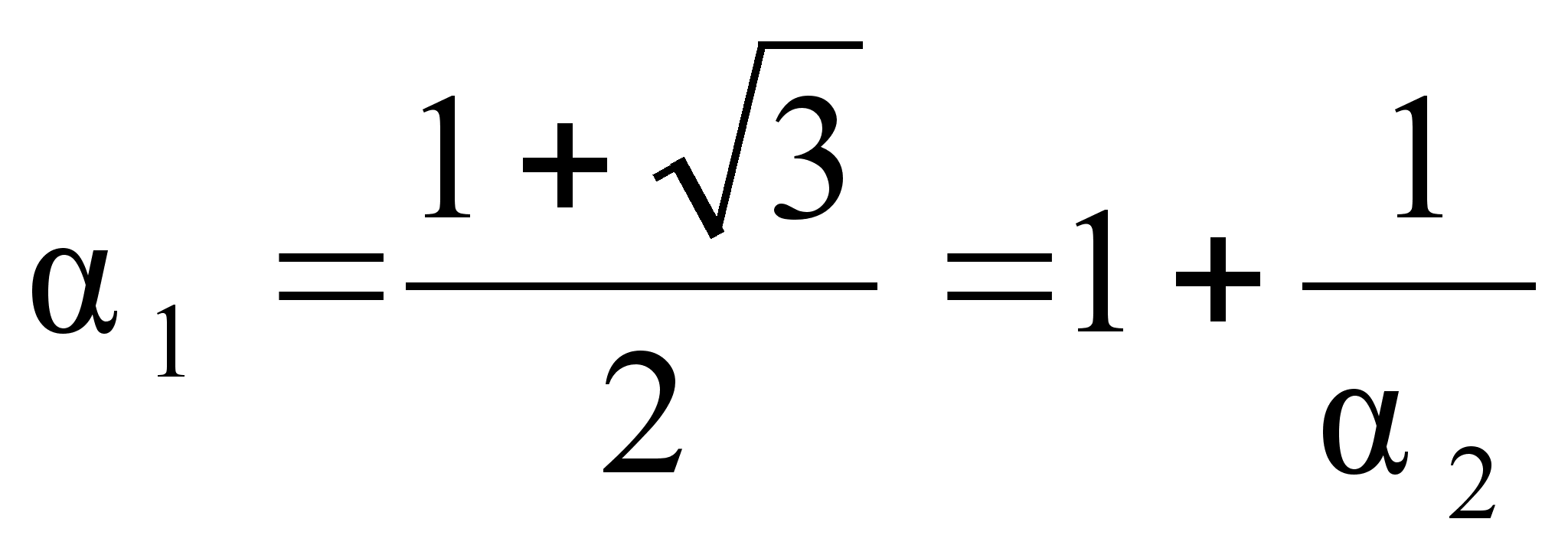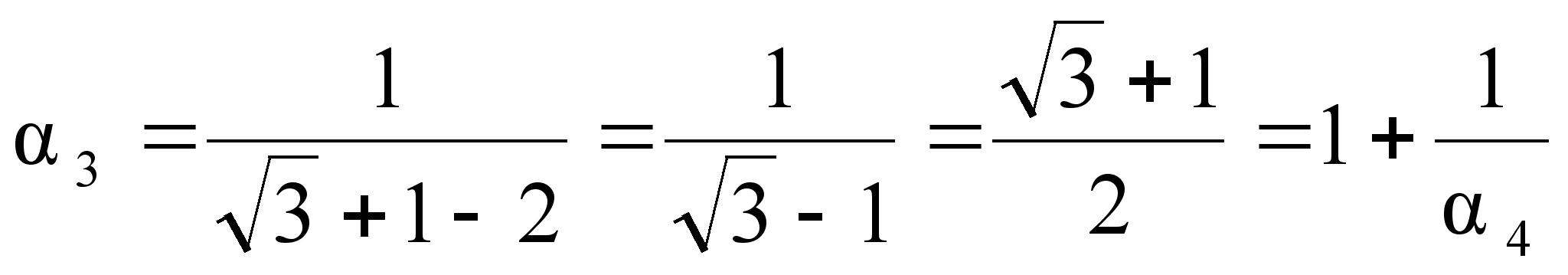=((1,
2))
| 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | |
|
| 1 | 3 | 4 | 11 | 15 | 41 | 56 | 153 | |
|
| 1 | 2 | 3 | 8 | 11 | 30 | 41 | 102 |
,
так как 30·41>1000.
Ответ:
.
7. Найти действительные числа, которые обращаются в данные цепные дроби:
a) (4, (3, 2, 1)); b) ((2, 1))
Решение:
a) (4, (3, 2, 1)) - смешанная периодическая дробь.
,
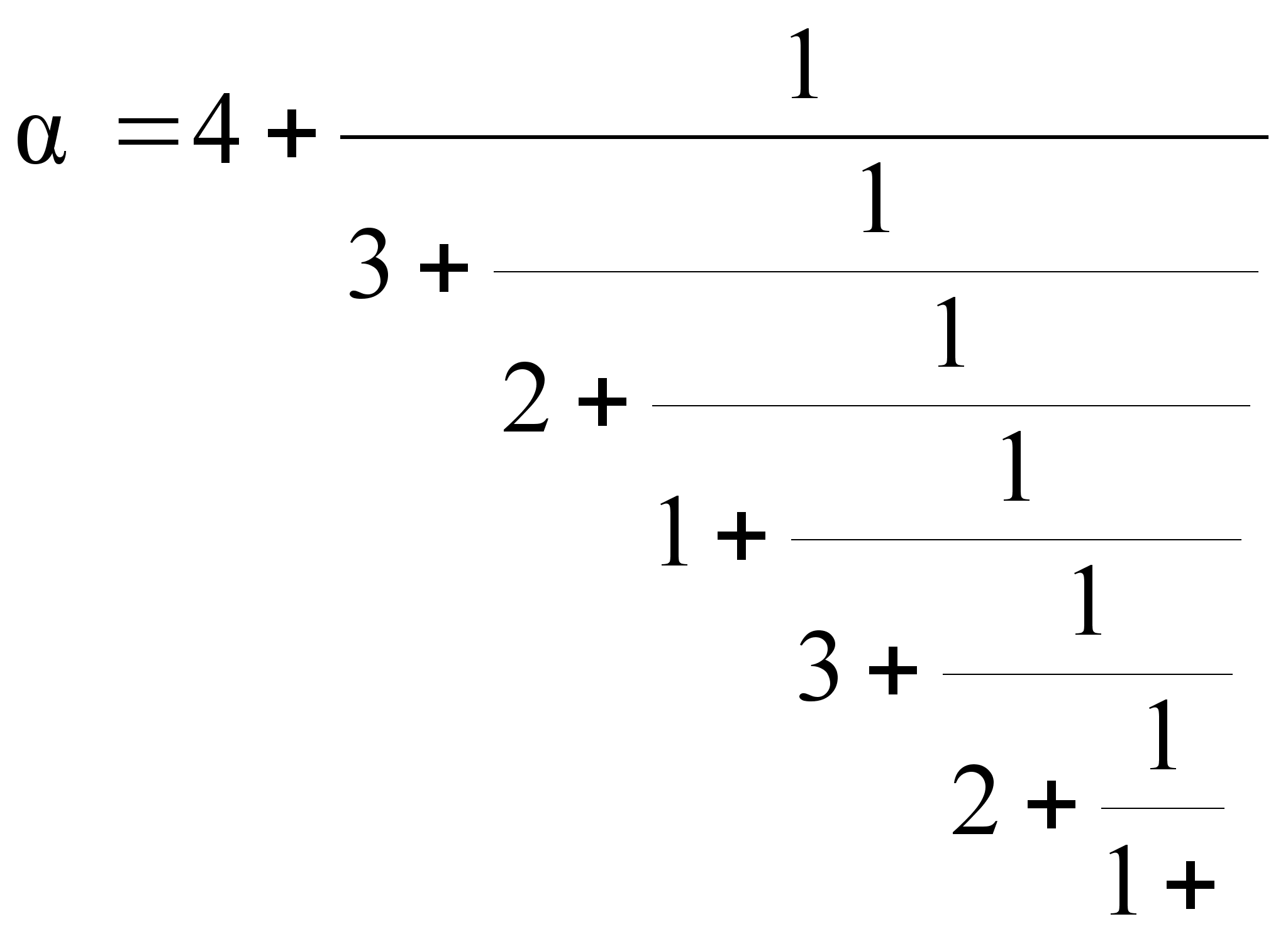
то есть 
,
где
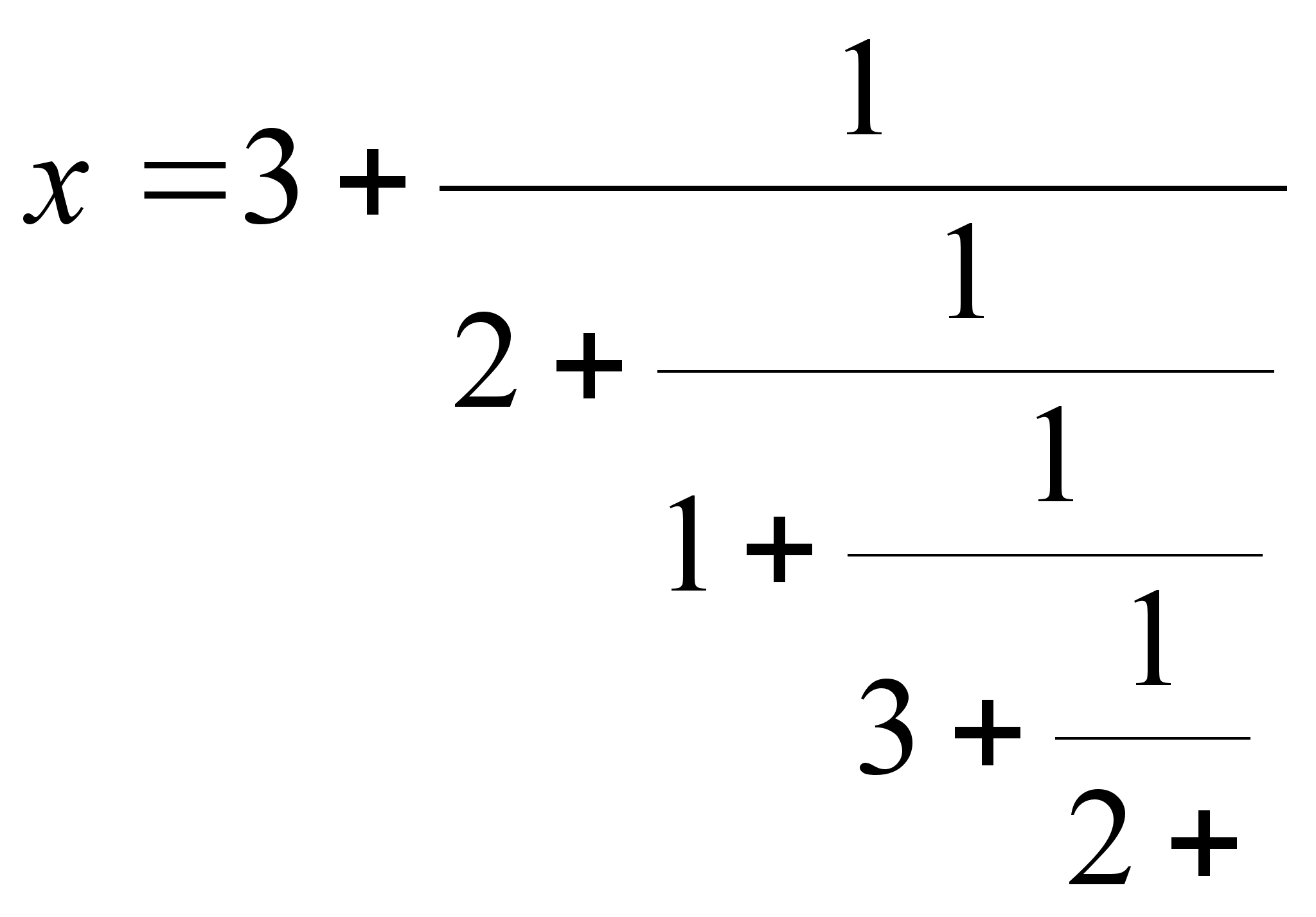
x=((3, 2, 1)) - чисто периодическая цепная дробь. Так как выражение, начинающееся с четвертого неполного частного 3, имеет тот же вид:
,
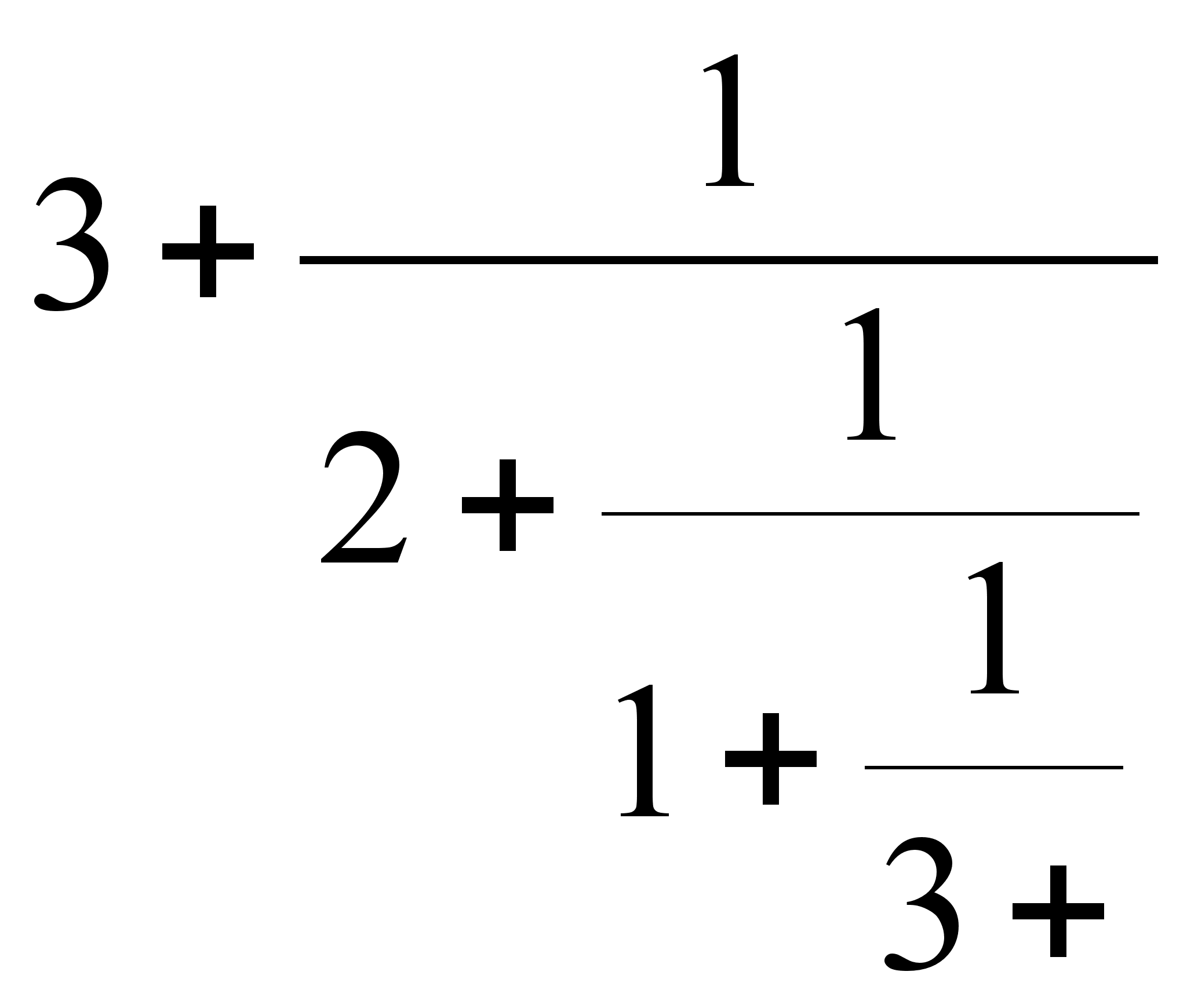
то мы можем
записать x=(3,
2, 1, x)=
=
,
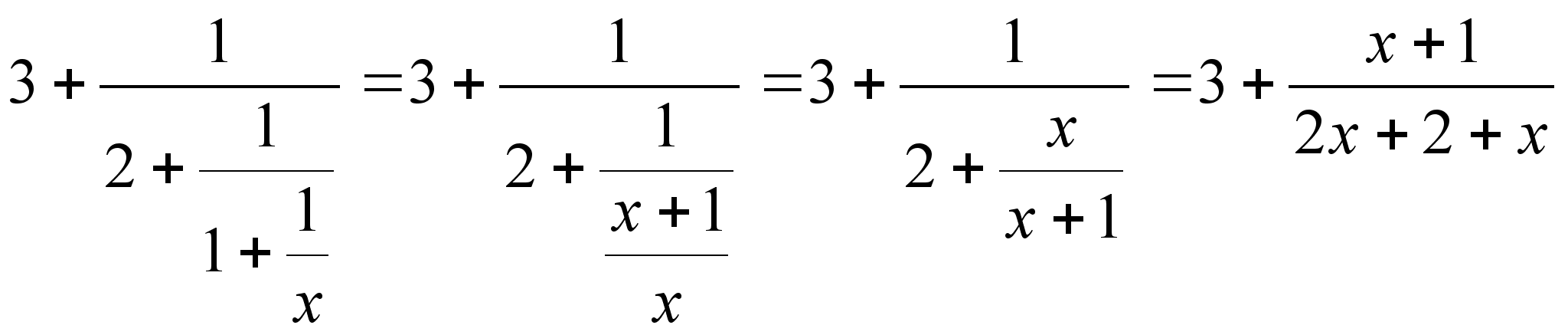после чего
приходим к
квадратному
уравнению
относительно
x:
D=64+12·7=148
.
Положительное
решение и есть
x.
.
Найдем
.
=4+
=
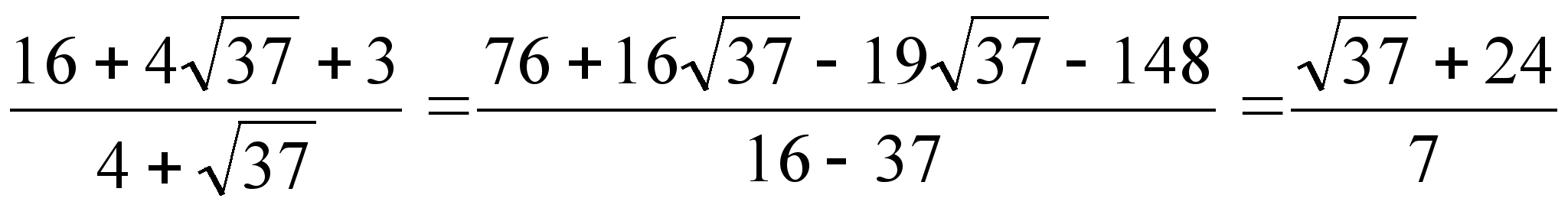
Ответ:
.
b)
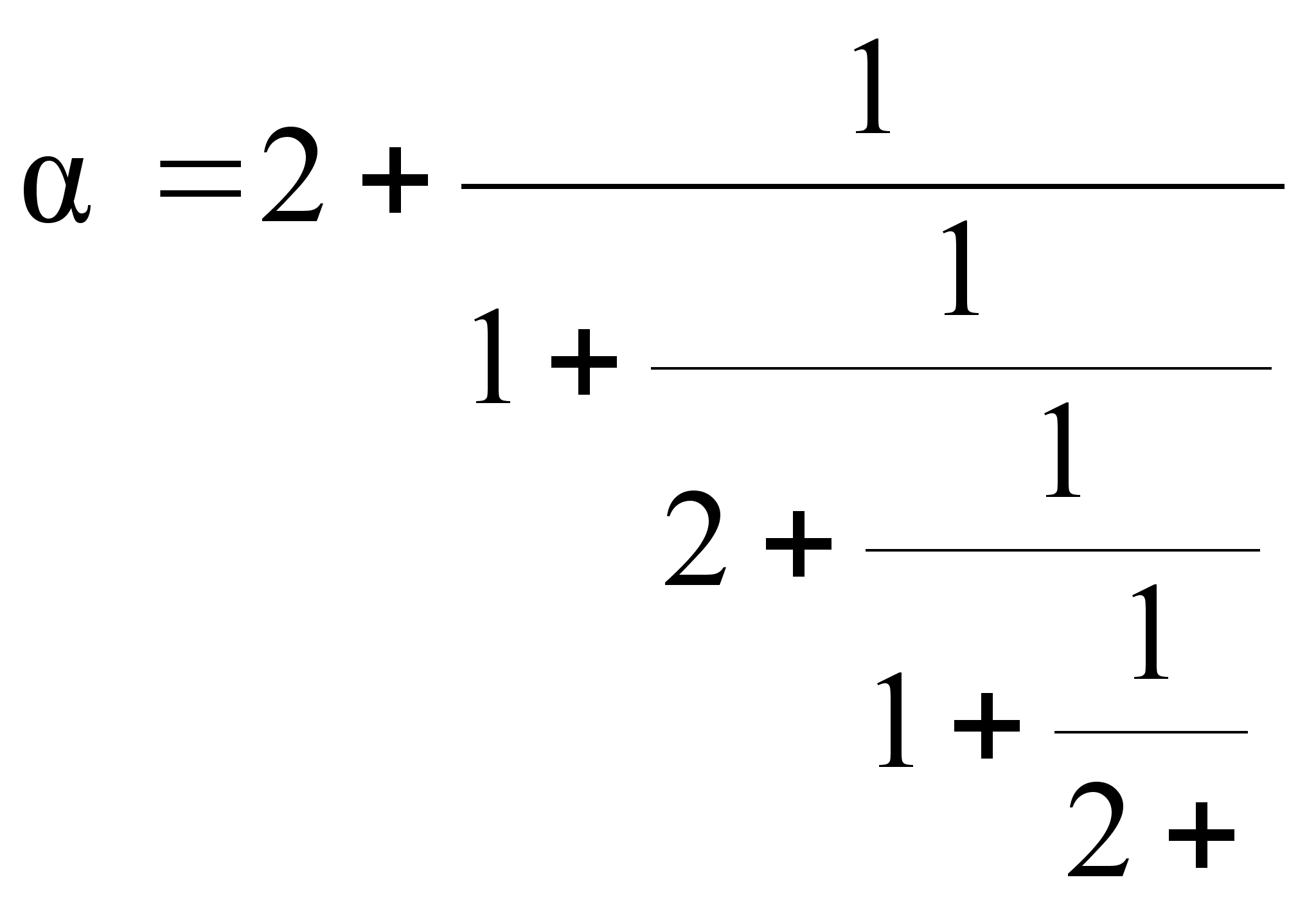
((2, 1))=
=(2,
1, )
Сейчас мы можем найти таким же путем, как и в задаче a), но можно решить задачу легче. Составим таблицу подходящих дробей:
| 2 | 1 |
| |
|
| 2 | 3 | 3 |
|
| 1 | 1 |
|
=
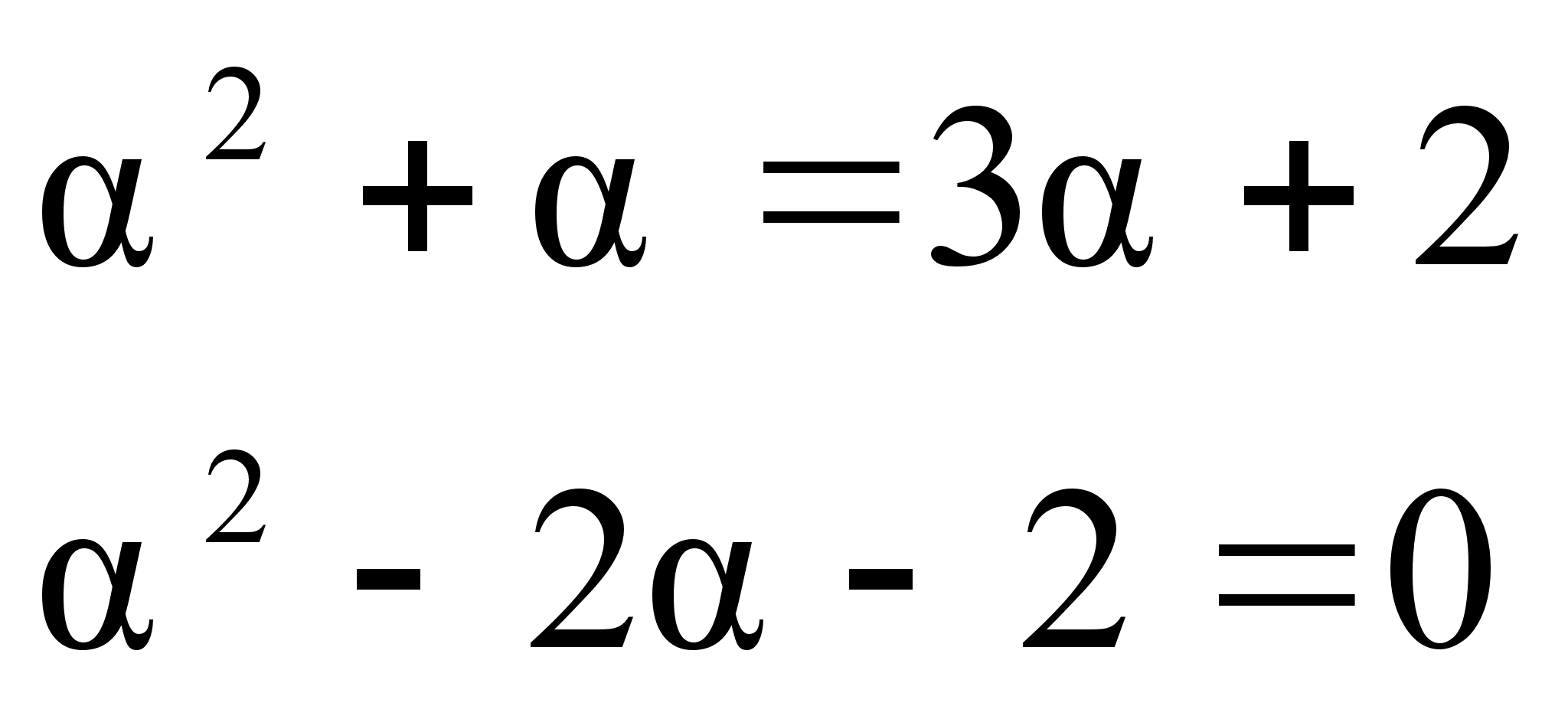
D=4+4·2=12
Положительное
решение и есть
искомое .
Ответ: 
.
8. Решить в целых числах уравнения:
a) 143x+169y=5; b) 2x+5y=7; c) 23x+49y=53.
Решение:
a) 143x+169y=5 - диофантово уравнение.
(143, 169)=13(НОД находим с помощью алгоритма Евклида)
уравнение
решений не
имеет.
Ответ:
.
b) 2x+5y=7
(2,
5)=1 
уравнение
имеет решение
в целых числах.
Разложим
в цепную дробь. =(0,
2, 2). Составим
все подходящие
дроби.
;
;
На
основании
свойства подходящих
дробей
получим
2·2-1·5
=(-1)3
или
2·2+5(-1)=-1
2·(-14)+5·7=7,
то есть
– частное решение.
Все решения могут быть найдены по формулам
или
c) 23x+49y=53
(23,
49)=1 
существуют
целые решения.
=(0,
2, 7, 1, 2)
, , 
, 
, 
17·23-8·49=(-1)5
23·17+49·(-8)=-1
23·(-901)+49·424=53
или 
Похожие работы
... из которых мультипликативна по лемме 2 пункта 13. Значит, ( a ) - мультипликативна. Следствие 3. . Доказательство. Пусть . Тогда, по лемме 1 пункта 13 имеем: . 5 Китайская теорема об остатках В этом пункте детально рассмотрим только сравнения первой степени вида ax b(mod m), оставив более высокие степени на съедение следующим ...
... так делаем, пока не закончатся элементы цепной дроби. Пример. Цепная дробь: [2,3,4,5] Рациональная дробь: 157/68 Тесты. 1.Некорректные данные 2.Корректные данные Заключение Разработана программа CalcKurs, выполняющая следующие функции: 1.формирование заданного подмножества натурального ряда с помощью общего делителя; 2.факторизация числа с опциями; 3.нахождение НОД и НОК ...
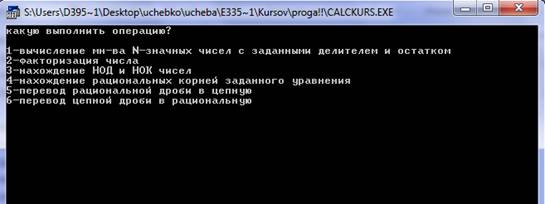
... ; q: char; begin writeln ('Дискретная математика'); writeln ('Курсовая работа, группа 03-119, каф308'); writeln ('выполнил: Тузов И.И. '); writeln ('руководитель: Гридин А.Н. '); writeln; writeln ('Калькулятор с функциями, описанными ниже'); writeln; Writeln ('Нажмите Enter'); readln; clrscr; repeat writeln ('Какую выполнить операцию? '); writeln; writeln ('1-вычисление мн-ва N- ...
... что если уравнение (25) имеет хотя бы одно решение, то оно имеет их бесчисленное множество. Нельзя, конечно, утверждать, что формулами (31) даются все решения уравнения (25). В теории алгебраических чисел доказывается, что все решения уравнения (25) в целых числах можно получить, взяв некоторое конечное и определенное зависящее от и число решений этого уравнения и размножив их с помощью формул ...
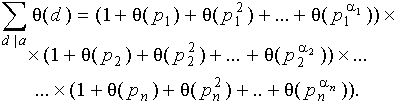
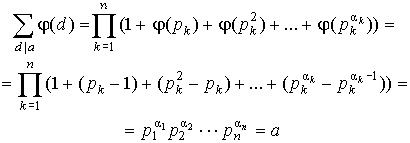
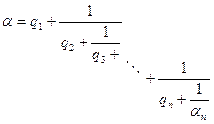
0 комментариев