Навигация
Развивать вычислительные навыки, речь, мышление, память
2. Развивать вычислительные навыки, речь, мышление, память.
3. Воспитывать самостоятельность активность , трудолюбие, любовь к математике.
Оборудование: карточку ax+by>c.
Ход урока.
I. Организационное начало урока.
-Здравствуйте, садитесь, сегодня урок алгебры проведу у вас я, зовут меня Елена Федоровна
II. Сообщение темы и цели.
-Сегодня, на уроке мы познакомимся с уравнениями нового вида - «Линейными уравнениями с двумя переменными».
III. Актуализация знаний учащихся.
-Посмотрите на доску. Какие из этих уравнений вам уже знакомы?
7х2+3х+5=0 5х+9=54
4х+9у=7 9(х2+6х+2)-8=30
x2/3+y2/2=1 4(х+2)+1=х+18.
-А как называются эти уравнения?
-Правильно это линейные уравнения с одной переменной.
-А кто скажет определение линейного уравнения с одной переменной?
-Уравнение вида ах=в, в котором x- переменная, а а и в – некоторые числа , называется линейным уравнением с одной переменной.
-Откройте учебники на стр. 27 , прочитайте это определение. Повтори…
-Приведите примеры линейных уравнений с одной переменной.
-Посмотрите на доску, перед вами линейные уравнения. Давайте вспомним как они решаются.
-Откройте тетради, запишите число, классная работа, тема: «Линейные уравнения с двумя переменными.»
-Все решают уравнения в тетрадях, а Оля пойдет к доске и решит с подробным объяснением первое уравнение:
2х+6=10
(Перенесем слагаемое без х в правую часть уравнения, изменив при этом его знак на противоположный: 2х=10-6 , вычислим результат 2х=4. Разделим обе части уравнения на 2, получим х=2).
-Молодец. Садись.
-Второе уравнение пойдет решать Саша.
2(х+3)+4=х-1.
(Раскроем скобки, для этого умножим 2 на каждое слагаемое суммы (х+3), получим 2х+6+4=х-1. Перенесем слагаемые, содержащие х в левую часть уравнения, а не содержащие х – в правую часть, изменив при этом знаки на противоположные.
2х-х= -6-4-1.
Приведем подобные слагаемые : х= - 11.
- Ребята , такие уравнения вы хорошо умеете решать.
- А какие свойства применяли при решении этих уравнений? (Если в уравнении слагаемое перенести из одной части в другую, изменив его знак , то получится уравнение, равносильное данному.)
- А какое еще свойство вы применяли? (Если разделить или умножить обе части уравнения на одно и тоже отличное от нуля число, то получится уравнение равносильное данному.)
IV. Изучение нового материала.
-Ребята, а сегодня мы познакомимся с уравнениями нового вида.
-Пусть известно , что одно их двух чисел на 5 больше другого. Если первое число обозначить буквой х, а второе буквой у, то соотношение между ними можно записать в виде равенства х-у=5, содержащего 2 переменные. Такие уравнения называются уравнениями с двумя переменными или уравнениями с двумя неизвестными.
-Уравнениями с двумя переменными также являются уравнения:
5х+2у=10, -7х+у=5, х2+у2=20 , ху=12 (запись на доске).
-Из этих уравнений первые два имеют вид ах+ву=с, где а, в, с – числа. Такие уравнения называются линейными уравнениями с двумя переменными.
-Итак: Линейным уравнением с двумя переменными называется уравнение вида ах+ву=с где х и у – переменные, а, в, с, - некоторые числа .
-Откройте учебники на странице 188.Прочитайте определение про себя.
-Теперь прочитайте вслух.
-А кто из вас повторит его ?
-уравнение х-у=5, при х=8, у=3. Обращается в верное равенство 8-3=5. Говорят, что пара значений переменных х=8, у=3 является решением этого уравнения. Записываю на доске:
х-у=5, х=8, у=3
8-3=5 - верное равенство.
Определение: Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство.
-Прочитайте это определение на странице 188 про себя.
-Прочитайте его вслух.
-Кто повторит? Повтори…
-А какие еще пары чисел будут являться решениями уравнения х-у=5? (х=105, у=100; х=4, у= -1,…)
-Правильно решениями этого уравнения будут являться числа, разность которых равно 5.
-Иногда пары значений переменных записывают короче: (105; 100), (4;- 1). ( Запись на доске).
-При такой записи необходимо знать, значение какой из переменных стоит на первом месте, а какой – на втором.
-в записи решений уравнения с переменными х и у на первом месте записывают значения х, а на втором – значение у.
-Уравнения с двумя переменными имеющие одни и те же решения, называют равносильными. уравнения с двумя переменными, не имеющие решений, также считают равносильными.
-Ребята, при решении линейных уравнений с одной переменной мы вспомним их свойства.
-Линейные уравнения с двумя переменными обладают такими же свойствами.
-Откройте учебники на стр. 189. Прочитайте эти свойства про себя.
-А теперь Таня , прочитай вслух. Повтори свойства.
-Рассмотрим уравнения 5х+2у=12.
-Воспользовались свойствами уравнений, выразим из этого уравнения одну переменную через другую , например у, через х. Для этого перенесем слагаемое 5х в правую часть уравнения изменив его знак.
2у= -5х+12.
-Разделим обе части этого уравнения на 2:
у= -2,5х+6
Уравнения 5х+2у=12 и
у= -2,5х+6 – равносильны.
-Пользуясь формулой у=2,5х+6, можно найти сколько угодно решений уравнения 5х+2у=12. Для этого достаточно взять произвольное х и вычислить соответствующее ему значение у.
Например: если х=2 , то у= -2,5.2+6=1.
если х=0,4 то у= -2,5*0,4+4=5.
Пары чисел (2; 1), (0,4; 5) – решение уравнения 5х+2у=12.Это уравнение имеет бесконечно много решений.
V .Первичное закрепление.
-Что же называется линейным уравнением с двумя переменными?
-Выполним № 1092 на странице 190 устно.
-Прочитай задание.
-Является ли первое уравнение 3х-у=17 линейным? (Да).
-Почему? (Т.к. имеет вид ах+ву=с)
-А второе упражнение? (Нет).
-Почему? (Т.к. уравнение х2- 2у=5 не приводится к виду ах+ву=с, х имеет показатель степени 2).
(Далее аналогично).
-А теперь запишите № 1094.
-Читай задание .
-Как ответить на этот вопрос? (Поставить значение х и у в уравнение. Если получится верное равенство, то х и у является решением уравнения)
-Все решайте в тетрадях, а……. у доски.
х + у=6
6=6 – верное равенство.
Ответ: да.
-А какие еще числа могут быть решениями этого уравнения х+у=6. (Дающие в сумме 6: 4 и 2, 3 и 3 и т.д.).
-Запишите любые 2 решения этого уравнения.
-Не забывайте, что значение х пишется на первом месте а у – на втором месте.
Самостоятельная работа.
-А теперь выполним № 1096. запишите.
-Прочитай задание.
-Что нужно сделать, чтобы ответить на вопрос? (Подставить значения х и у в уравнение и посмотреть, получится ли верное равенство).
а) .Организация самостоятельной работы.
-Все решают в тетрадях, а к доске пойдут Лена и Оля.
-Саша проверит первые 2 пары, а Катя вторые 2 пары.
-А потом проверим.
б) Проведение самостоятельной работы.
(3; 1 ) (0; 10)
3*3+1>10 3*0+10=10.
10=10 – верное равенство 10=10 верное равенство
Ответ: является Ответ: является
(2; 4) (3; 2,5)
3*2+4=10 3*3+2.5=10
10=10 – верное равенство 11,5=10 – неверное равенство
Ответ: является Ответ: не является.
в) Проверка самостоятельной работы.
-Давайте проверим правильно ли выполнила Оля.
-У кого другой ответ?
-А Лена?
-У кого другой ответ?
-Молодцы. Садитесь.
-А теперь выполним № 1099.
-Прочитай задание.
-Что нужно сделать, чтобы выразить у через х? (Представить, что х известное число и найти у )
-Пойди к доске реши с объяснением, а все решают в тетрадях.
4х-3у=12.
(Одночлен 3у является неизвестным вычитаемым. Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность 3у=4х-12 .
Разделим обе части уравнения на 3, получим:
-Молодец. Садись.
А теперь выполним пункт б, Сережа иди к доске.
4х-3у=12.
(Одночлен 4х является неизвестным уменьшаемым, чтобы его найти, надо к разности прибавить вычитаемое: 4х=12+3у. Разделим обе части уравнения на 4 и получим:
-Правильно. Молодец. Садись .
VI. Подведение итогов.
-Какой вид имеет линейное уравнение с двумя переменными ? (ах+ву=с).
-Что называется решением линейного уравнения с двумя переменными ?
-Приведите примеры таких уравнений.
-Какими свойствами обладают уравнения с двумя переменными?
2 К тренировочным относятся задания на распознавание различных объектов и их свойств. Тренировочные самостоятельные работы состоят из однотипных заданий, содержащих существенные признаки и свойства данного определения, правила. Конечно, эта работа мало способствует умственному развитию детей, но она необходима, так как позволяет выработать основные умения и навыки и тем самым создать базу для дальнейшего изучения математики.
При выполнении тренировочных самостоятельных работ учащимся еще необходима помощь учителя. Можно разрешить пользоваться и учебником, и записями в тетрадях, таблицами и т. п. Все это создает благоприятный климат для слабых учащихся. В таких условиях они очень легко включаются в работу и выполняют ее.
| Тема: | Решение текстовых задач при помощи систем уравнений, содержащих уравнения второй степени. |
|
| |
| Цель: | Расширение и углубление знаний, формирование умений решать системы, повышенной сложности, уметь составлять системы по условию задачи: Развивать устойчивый интерес к предмету, умение самостоятельно работать; Воспитывать умение осуществлять индивидуальную мыслительную деятельность; |
| Оборудование: | Учебник, «сборники заданий по математике» Кузнецов Л. В.; |
Ход урока:
I. Организационное начало урока:
II. Сообщение темы и цели: - Сегодня на уроке продолжим решать системы уравнений, но будем учиться сами составлять по задаче систему.
III. Актуализация знаний учащихся: - Запишите число, тему.
1) выразить одну неизвестную через другую:
| 1. 3х-у=3 -у=3-3х у=3х-3 | 2. у+2х=2 2х=2-у |
| 2) решить систему методом подстановки:
| |
| - Повторим алгоритм. Решим: | |
Решим квадратное уравнение:
или
или
Ответ: (4; -14); (-1; 1)
IV. Закрепление
№ 498
-Прочтите задачу
-Как обозначим числа? (х, у)
-Если сумма? (х+у=18)
-Произведение чисел? (х*у=65)
-Найти что? (эти числа)
-Какую систему получим?
-Каким методом будем решать?
(записать пояснение: Пусть первое число – х и т. д.)
-К доске пойдет….
Решим квадратное уравнение:
Ответ: числа 5 и 13.
№504
-Прочтите условие.
-Какой формы участок? (Прямоугольной)
-Пусть длина – х, ширина – у.
-Площадь прямоугольника? (S=ав)
-Нужно перевести в одну единицу измерения: км. в м., га. в м2;
-Если участок прямоугольной формы, то какое уравнение составим?
(2(х+у)=1000)
-Площадь участка 60000 м2? (ху=60000)
-Запишем условие к задаче:
Пусть длина участка – х, ширина – у. Так как участок надо огородить забором длиной 1000м. Так как площадь участка 60000 м2, то составим уравнение: ху=60000. Получим систему:
Þ
Ответ: длина – 300м., ширина – 200м.
№ 1
-Послушайте условие:
«Одно из двух положительных чисел на 3 больше другого. Найдите эти числа, если их произведение равно 70?»
-Пусть числа х и у.
-Если известно, что одно больше на 3. Как запишем? (х=у+3)
-Произведение чисел? (ху=70)
-Составим систему:
Решим квадратное уравнение:
так как числа положительные, то 10 и 7.
Ответ: 10 и 7.
2) самостоятельная работа. (15 мин.)
-У вас на партах лежат сборники заданий и у каждого номер индивидуального задания.
-Запишите: «Самостоятельная работа»., стр… №….
| 1. | С. 15, в-1, № 3 С. 11, в-1, №4 | 2. | С. 20, в-1, № 5 С. 19, в-1, №4 |
| 3. | С. 28, в-1, № 6 С. 11, в-1, №4 | 4 | С. 35, в-1, № 3 С. 19, в-1, №4 |
| 5. | С. 48, в-1, № 6 С. 19, в-1, №4 | 6 | С. 21, в-1, № 6 С. 19, в-2, №4 |
| 7. | С. 15, в-2, № 3 С. 11, в-2, №4 | 8. | С. 20, в-2, № 5 С. 19, в-2, №4 |
| 9. | С. 28, в-2, № 6 С. 11, в-2, №4 | 10. | С. 35, в-2, № 3 С. 19, в-2, №4 |
| 11. | С. 48, в-2, № 6 С. 19, в-2, №4 | 12. | С. 21, в-2, № 6 С. 11, в-1, №4 |
| 13. | С. 29, в-1, № 4 С. 11, в-1, №4 | 14. | С. 29, в-2, № 4 С. 11, в-1, №4 |
| 15. | С. 30, в-2, № 6 С. 11, в-2, №4 | 16. | С. 31, в-2, № 6 С. 19, в-1, №4 |
| 17. | С. 30, в-1, № 6 С. 19, в-2, №4 | 18. | С. 31, в-1, № 6 С. 11, в-1, №4 |
-Оцениваться будут каждое задание отдельно.
Ответы
| 1. | 1) (-5; 2); (2; -5) | 10. | 1) (5; -3); (-3; 5) |
| 2. | 1) (-2; 1); (1; -2) | 11. | 1) (1; -3); (3; -1) |
| 3. | 1) (5; -3); (-3; 5) | 12. | 1) (-7; 11); (3; 1) |
| 4. | 1) (8; 4); (4; 8) | 13. | 1) (7; 6); (-3; -4) |
| 5. | 1) (2; -4); (4; -2) | 14. | 1) (-7; -9); (3; 1) |
| 6. | 1) (-7; 9); (4; -2) | 15. | 1) (-3; 7); (2; 2) |
| 7. | 1) (-3; 4); (-4; 3) | 16. | 1) (2; 4); (4; 2) |
| 8. | 1) (2; 3); (3; 2) | 17. | 1) (-2; -3); (1; 0) |
| 9. | 1) (-2; 7); (7; -2) | 18. | 1) (6; -4); (-4; 6) |
V. Подведение итогов:
-сколько существует способов решения систем уравнений?
-сдайте тетради.
3 К закрепляющим можно отнести самостоятельные работы, которые способствуют развитию логического мышления и требуют комбинированного применения различных правил и теорем. Они показывают, насколько прочно, осмысленно усвоен учебный материал. По результатам проверки заданий данного вида учитель определяет, нужно ли еще заниматься данной темой.
Тема: Графический способ решения уравнений.
Цель: добиться осознанного усвоения и запоминания графического
способа решения уравнений, сформировать практические умения и навыки;
Воспитывать аккуратность ;
Развивать наглядные представления;
Оборудование: табличка «абсцисса», таблица с графиками.
Ход урока.
I. Организационное начало.
а) Приветствие
б) Проверка готовности рабочих мест.
II. Сообщение темы и цели.
- Сегодня мы с вами научимся решать уравнения с помощью графиков.
III. Актуализация знаний учащихся.
Похожие работы
... и практическое использование различных форм уроков математики Для того чтобы доказать или опровергнуть, что использование различных форм уроков способствует улучшению качества знаний школьников по теме "Квадратные уравнения", были разработаны и проведены разнообразные формы уроков в 8 классе МОУ “Иштеряковская средняя общеобразовательная школа". При изучении темы были выбраны такие формы ...
... , можно сделать вывод о недостаточном освещении изучаемого вопроса в современной методической литературе. Объект исследования работы: процесс обучения математике. Предмет: формирование умения решения квадратных уравнений у учащихся 8-го класса. Контингент: учащиеся 8-го класса. Глава 1. Теоретические аспекты обучению решения уравнений в 8 классе 1.1. Из истории возникновения квадратных ...
... работа как прием обучения может входить почти во все методы обучения, воспитывать в учениках потребность самостоятельно добывать знания, умение творчески пользоваться объяснениями учителя, помощью товарищей, книгами, конспектами одна из важнейших целей нашей работы.ГЛАВА 2. ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИЙ ПРИЁМЫ И МЕТОДЫ §1. Анализ программ и учебников «Алгебра, 7», «Алгебра, ...
... работа оказывает значительное влияние на глубину и прочность знаний учащихся по предмету, на развитие их познавательных способностей, на темп усвоения нового материала. Практический опыт учителей многих школ показал, что: 1. Систематически проводимая самостоятельная работа (с учебником по решению задач, выполнению наблюдений и опытов) при правильной ее организации способствует получению ...
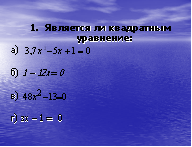


0 комментариев