Последовательно возрастающих таких рядов составляют цикл. Исключением является первый цикл, в котором количество эманационных рядов равно n + 1
Принцип противоположности натуральных корней и их эманаций
Если х > у ,а |х < |у
Деление эманаций натурального корня n на эманации натурального корня k
Циклы натуральных корней умножения
Навигация
Последовательно возрастающих таких рядов составляют цикл. Исключением является первый цикл, в котором количество эманационных рядов равно n + 1
Настоящая теория чисел
63167
знаков
2
таблицы
0
изображений
10 последовательно возрастающих таких рядов составляют цикл. Исключением является первый цикл, в котором количество эманационных рядов равно n + 1.
Аналогичным образом, на основе циклов, можно сформировать периоды, эоны и еще более значительные цикличные последовательности эманаций. Таким образом, становится очевидным, что весь натуральный числовой ряд имеет собственные законы развития, а каждый натуральный корень продолжается в своих эманациях.
2.3. Свойства эманационных рядов и циклов.
1) Эманационные ряды и циклы образуются путем последовательного прибавления числа 9 к натуральному корню n;
2) k-ый эманационный ряд имеет обобщающее число z, образующееся сложением двух чисел p и m, где p - эманация числа n, взятая без последней цифры m; k-ый эманационный цикл имеет обобщающее число z, образующееся сложением двух чисел p и m, где p - эманация числа n, взятая без последней цифры m;
3) Столбцы эманаций натурального корня n, где n=[0,1,2,..,.8], имеют ряд следующих свойств:
- эманации при рассмотрении от первого к последнему столбцу имеют в окончании своего числа цифру, изменяющуюся последовательно на единицу от 9 до 0, причем в первом столбце эманации оканчиваются на цифру 9, а в последнем на 0;
- разница между ближайшими числами столбца равна 90;
- первая цифра в числе эманации при рассмотрении от одной к другой в столбце увеличиваются на 1, а следующая за ней уменьшается на 1.
Более удобным для применения, на наш взгляд, является следующий принцип построения таблиц эманаций натурального корня n. В вертикальных рядах таблицы объединены такие эманации натурального корня n, номера эманаций которых (см. далее) равны по натуральному корню.
Например. Эманации натурального корня 7 - числа 106 и 268 имеют номера эманаций 11 и 29 соответственно, натуральный корень 106 и 268 равен 2.
Правило 1. При сложении двух или нескольких чисел, натуральный корень суммы которых < 9, сумма номеров эманаций складываемых чисел будет равна номеру эманации полученной суммы. Если же натуральный корень суммы > или = 9, то номер эманации суммы будет на единицу больше суммы номеров эманаций складываемых чисел.
Это легко объяснимо, т.к. любое число мы можем представить в виде abcd...n = Nэ * (9 + n), где n - натуральный корень этого числа. Таким образом, при сложении чисел мы складываем отдельно количество 9-к и натуральные корни, и, если натуральные корни в сумме дадут число больше 9, мы вычленяем 9-ку и прибавляем ее к уже имеющимся.
Например.
Сложим числа 199 и 49:
199 + 49 = 248.
Nэ числа 199 равен 22, Nэ числа 49 равен 5, Nэ полученной суммы 248 равен 27, т.е. сумме 22 и 5, т.к. сумма натуральных корней меньше 9
1|199 + 4|49 = 5|248 .
Сложим числа 145 и 233:
145 + 233 = 378.
Nэ числа 145 равен 16, Nэ числа 233 равен 25, Nэ полученной суммы 378 равен 42, т.е. 16 + 25 +1, т.к. сумма натуральных корней равна 9
Теорема 1.
При делении любого целого многозначного числа abcd...k на число 9 полученный результат будет указывать:
а) в целой части - на номер эманации;
б) в дробной, всегда образующей период, на натуральный корень.
Доказательство.
При делении числа abcd...k на 9 мы всегда получаем число, имеющее целую часть и дробный период. Докажем, что полученный результат будет указывать:
а) в целой части - на номер эманации;
б) в дробной, всегда образующей период, на целый остаток за вычетом целого количества девяток.
В силу того, что 1/9=0,1(1), заменим деление числа abcd...n на 9 на умножение на 0,111(1).
Разложим число abcd...k как abcd...k = n9 + x Умножим обе части уравнения на 0,1(1) :
abcd...k * 0,1(1)= n9*0,1(1) + x0,1(1).
Зная, что 1/9=0,1(1), т.е. 9*0,1(1)=1, n9*0,1(1) будет равно n, т.е. n9*0,1(1)=n.
Поскольку х меньше 9, то x*0,1(1) меньше 1 и x*0,1(1)= х(х).
Тогда abcd...k * 0,1(1)= abcd...k /9= n9*0,1(1) + x0,1(1)=n + 0,х(х)= n,х(х).
Так как n обозначает количество девяток в числе abcd...k , т.е. является номером эманации числа, то остаток х является самим натуральным корнем и, соответственно, при делении любого целого многозначного числа
abcd...k на число 9 полученный результат n,х(х) в целой части n показывает номер эманации, а в дробной х(х) , всегда образующей период, на натуральный корень.
Пример 1.
Найти номер эманации и натуральный корень числа 2852. Разделим данное число на 9:
2852 : 9 = 316,8(8).
Исходя из вышеуказанной теоремы, предположим, что
|2852 = 8, а номер эманации равен 316.
Проверим полученный результат.
2852 = 28 + 52 = 80, => |2852 = 8
Правильность номера эманации можно проверить на основании таблиц Приложения 1.
Пример 2. Найти номер эманации и натуральный корень числа 23.
23 : 9 = 2,5(5) => |23 = 5, а номер эманации равен 2.
Пример 3. Найти номер эманации и натуральный корень числа 18.
Произведем аналогичные вышеизложенному операции.
18 : 9 = 2.
Из этого примера видно, что число 9 само является второй эманацией числа (не-числа) 0, ибо полученный ответ необходимо записать в следующей форме 18 : 9 = 2,0(0), откуда видно, что число 18 является второй эманацией нуля.
Проверим это утверждение на двух других примерах.
Разделим саму девятку на число 9:
9 : 9 = 1,0(0), т.е. число 9 является первой эманацией нуля.
15921 : 9 = 1769,0(0), т.е. число 15921 является 1769-й эманацией нуля.
Из нашего утверждения относительно числа 9 и всего вышесказанного можно сделать следующие выводы:
- весь числовой ряд разбит на циклы, состоящие из десяти чисел таких, как: от 0 до 9, от 9 до 18, от 18 до 27 и т.д., хотя основных натуральных корней всего 9, такая система применяется в силу того, что любая эманация нуля является как завершением предыдущего цикла, так и началом следующего;
- последовательное возрастание числового ряда на 1, начиная с любого многозначного числа, неуклонно "отслеживается" изменением натурального корня, являющегося проекцией бесконечного ряда чисел.
Похожие работы
... мест. Методы Коши получили всеобщее распрастранение, применялись оттачивались весь XIX век. Идеи и методы Коши плодотворно пользуются и обобщаются современными математиками и сегодня. 4 Создание теории действительного числа После «наведения порядка» в математическом анализе встал вопрос о ситуации в арифметике. «К необходимости разработки теории действительных чисел приводили многие задачи ...
... из которых мультипликативна по лемме 2 пункта 13. Значит, ( a ) - мультипликативна. Следствие 3. . Доказательство. Пусть . Тогда, по лемме 1 пункта 13 имеем: . 5 Китайская теорема об остатках В этом пункте детально рассмотрим только сравнения первой степени вида ax b(mod m), оставив более высокие степени на съедение следующим ...
... получаются экспериментальная и теоретическая зависимости P (j, l), сходимость которых проверяется по известным критериям, причем проверку целесообразно проводить при разных значениях l и р, 0 < р < 1. 7. Генератор случайных чисел в Borland C++ В языке C, как и во многих других языках высокого уровня, существует встроенная поддержка генератора случайных чисел. Для формирования чисел ...
... предшественников, накопленного в течении тысячелетий, что свидетельствует об интенсивности, динамизме их математического познания. Качественное отличие исследований Фалеса и его последователей от догреческой математики проявляется не столько в конкретном содержании исследованной зависимости, сколько в новом способе математического мышления. Исходный материал греки взяли у предшественников, но ...
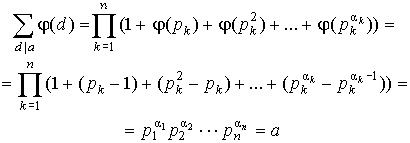
0 комментариев