Синтез микропрограммного управляющего автомата

Министерство общего и профессионального образования РФ

Вятский государственный технический университет

Факультет автоматики и вычислительной техники

Кафедра электронных вычислительных машин

ДОПУСКАЮ К ЗАЩИТЕ Руководитель работы _______ О.А. Залетов

СИНТЕЗ МИКРОПРОГРАММНОГО

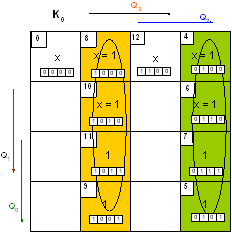
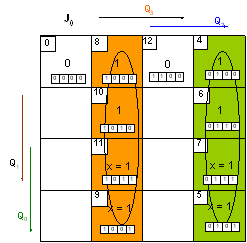
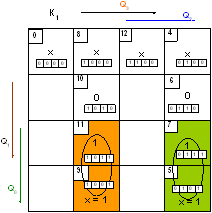
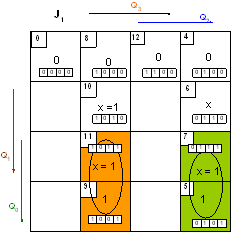
УПРАВЛЯЮЩЕГО АВТОМАТА

Пояснительная записка

курсовой работы

по теории автоматов

ТПЖА.220100.22.29 ПЗ

Разработал студент гр. ВМ-22 ( _______ ) Р.В. Гонта

Проверил преподаватель кафедры ЭВМ ( _______ ) О.А. Залетов

Нормоконтролер ( _______ ) В.Ю. Мельцов

Председатель комиссии ( _______ ) В.Д. Матвеев

Члены комиссии ( _______ ) В.Ю. Мельцов

Работа защищена с оценкой ( _______ )

1999

Содержание

Введение 1 Постановка задачи 2 Описание используемого алгоритма умножения 2.1 Алгоритм умножения чисел в форме с ПЗ с простой коррекцией 2.2 Алгоритм умножения первым способом 3 Ручной подсчет 4 Выбор и описание структурной схемы ОА 5 Реализация содержательной ГСА 6 Построение отмеченной ГСА 7 Синтез МПА в соответствии с моделью Мили 7.1 Построение графа автомата 7.2 Построение прямой структурной таблицы переходов и выходов 7.3 Кодирование на D-триггерах 7.4 Получение логических выражений для функций возбуждения D-триггеров и функций выходов 7.5 Кодирование на RS-триггерах 7.6 Получение логических выражений для функций возбуждения RS-триггеров 7.7 Кодирование на T-триггерах 7.8 Получение логических выражений для функций возбуждения T-триггеров 7.9 Кодирование на счетчике 7.10 Получение уравнений для счетчика 8 Синтез МПА в соответствии с моделью Мура 8.1 Построение графа автомата 8.2 Построение прямой структурной таблицы переходов и выходов 8.3 Кодирование на D-триггерах 8.4 Получение логических выражений для функций возбуждения D-триггеров и функций выходов 8.5 Кодирование на RS- триггерах 8.6 Получение логических выражений для функций возбуждения RS- триггеров и функций выходов 9 Построение функциональной схемы микропрограммного управляющего автомата Заключение Библиографический список Перечень сокращений

УДК 681.3

Реферат

Гонта Р.В. Синтез микропрограммного управляющего автомата. Курсовая работа / ВятГТУ, каф. ЭВМ, рук. О.А. Залетов – Киров, 1999. Гр. ч. 3 л. ф. А2

ОПЕРАЦИОННЫЙ АВТОМАТ, МИКРОПРОГРАММНЫЙ УПРАВЛЯЮЩИЙ АВТОМАТ , ГРАФ-СХЕМА АЛГОРИТМА, ГРАФ, ФУНКЦИОНАЛЬНАЯ СХЕМА, МОДЕЛЬ МИЛИ, МОДЕЛЬ МУРА

Цель работы — синтезировать микропрограммный автомат, управляющий операцией умножения чисел в форме с плавающей запятой и характеристикой в дополнительном коде первым способом с простой коррекцией.

Результатом работы является создание функциональной схемы микропрограммного управляющего автомата.

 Введение

Потребность в вычислениях возникла у людей на самых ранних стадиях развития человеческого общества. Причем с самого начала для облегчения счета люди использовали различные приспособления. Многие из них были весьма интересными и остроумными по принципу действия, но все они обязательно требовали, чтобы в процессе вычислений активно участвовал человек-оператор. Качественно новый этап развития вычислительной техники наступил с изобретением и созданием электронных вычислительных машин, которые работают автоматически, без участия человека, в соответствии с заранее заданной программой. Появление таких машин вызвано объективными условиями современного развития науки, техники и народного хозяйства. Во многих областях человеческой деятельности уже в середине ХХ века объем и сложность вычислительных работ настолько возросли, что решение некоторых задач без применения вычислительной техники было бы практически не возможным. В настоящее время электронные вычислительные машины применяются во многих областях науки, техники и народного хозяйства. В основном они используются: для решения сложных математических и инженерных задач, в качестве управляющих машин в промышленности и военной технике, в сфере обработки информации.

1 Постановка задачи

Требуется разработать МПА, управляющий операцией умножения двоичных чисел в форме с плавающей запятой и характеристикой в дополнительном коде первым способом с простой коррекцией.

Функциональную схему устройства построить в основном логическом базисе. Операнды разрядностью 4 байта (тридцать два разряда) поступают по входной шине (ШИВх) в дополнительном коде (ДК), результат также в ДК выводится по выходной шине (ШИВых). В младших 24 разрядах операнда хранится мантисса со знаком, а в следующих 8 разрядах - характеристика.

2 Описание используемого алгоритма умножения

Процесс умножения состоит из последовательности операций сложения и сдвигов.

2.1 Алгоритм умножения чисел в форме с ПЗ с простой коррекцией

1.    Определить знак произведения сложением по модулю два знаковых разрядов сомножителей.

2.    Перемножить модули мантисс сомножителей по правилам с ФЗ:

2.1. Выполнить коррекцию, если хотя бы один из сомножителей отрицательный по правилу введения коррекции.

Правила введения коррекции при умножении чисел в ДК:

-      Если сомножители положительны, коррекции нет.

-      Если один из сомножителей отрицателен, к псевдопроизведению надо прибавить ДК от модуля положительного сомножителя.

-      Если оба сомножителя отрицательны, к псевдопроизведению надо прибавить ДК от модулей дополнительных кодов обоих сомножителей, то есть их прямые коды.

2.2. Перемножить модули сомножителей, представленных в ДК, одним из четырех способов получить псевдопроизведение.

3.    Определить характеристику произведения алгебраическим сложением характеристик сомножителей.

4.    Нормализовать мантиссу результата и выполнить округление если необходимо.

2.2 Алгоритм умножения первым способом

Умножение с младших разрядов множителя со сдвигом частных сумм вправо.

В каждом такте цикла умножения первым способом необходимо:

2.1 Сложить множимое с предыдущей частной суммой, если очередной разряд множителя равен 1, и результат (новую частную сумму) запомнить; в случае если очередной разряд множителя равен 0 суммирование не выполнять;

2.2 Уменьшить вдвое частную сумму, что равносильно сдвигу ее на один разряд вправо.

3 Ручной подсчет

Выполним ручной подсчет в соответствии с выше указанным алгоритмом.

В качестве множителя возьмём число 9, а в качестве множимого 13.

3.1 Сомножители положительные (A>0, B>0)

A = 9 = 1001₂, А_пк = 0,1001, А_дк = 0,1001

B = 13= 1101₂, В_пк = 0,1101, В_дк = 0,1101

3.1.1 Определим знак произведения: 0 + 0 = 0

3.1.2 Перемножим модули сомножителей:

Таблица 1

Множимое	Множитель	Сумматор	Пояснения
0,1101	0,1001	0,00000000 0,11010000 0,11010000	Сложение
		0,01101000	Сдвиг
	0,0100	0,00110100	Сдвиг
	0,0010	0,00011010	Сдвиг
	0,0001	0,00011010 0,11010000 0,11101010	Сложение
		0,01110101	Сдвиг

Получили псевдопроизведение: 0,01110101

3.1.3 Коррекция не нужна, так как оба множителя положительные.

3.1.4 Присвоение произведению знака:

(A*B)_дк=0,01110101

(A*B)_пк=0,01110101

A*B = (9)*(13) = 117 = 1110101₂

3.2 Сомножители разных знаков (А<0, B>0)

 A =-9=-1001₂, А_пк = 1,1001, А_дк = 1,0111

 B =13= 1101₂, В_пк = 0,1101, В_дк = 0,1101

3.2.1 Определим знак произведения: 1 + 0 = 1

3.2.2 Перемножим модули сомножителей:

Таблица 2

Множимое	Множитель	Сумматор	Пояснения
0,1101	0,0111	0,00000000 0,11010000 0,11010000	Сложение
		0,01101000	Сдвиг
	0,0011	0,01101000 0,11010000 1,00111000	Сложение
		0,10011100	Сдвиг
	0,0001	0,10011100 0,11010000 1,01101100	Сложение
		0,10110110	Сдвиг
	0,0000	0,01011011	Сдвиг

Получили псевдопроизведение: 0,01011011

3.2.3 Произведём коррекцию (прибавим к псевдопроизведению В_дк):

0,01011011

В_дк= 0,00110000

0,10001011

3.2.4 Присвоение произведению знака:

(A*B)_дк=1,10001011

(A*B)_пк=1,01110101

A*B = (-9)*(13) = -117 = -1110101₂

3.3 Сомножители разных знаков (А>0, B<0)

A = 9 =  1001₂, А_пк = 0,1001, А_дк = 0,1001

 B =-13= -1101₂, В_пк = 1,1101, В_дк = 1,0011

3.3.1 Определим знак произведения: 0 + 1 = 1

3.3.2 Перемножим модули сомножителей:

Таблица 3

Множимое	Множитель	Сумматор	Пояснения
0,0011	0,1001	0,00000000 0,00110000 0,00110000	Сложение
		0,00011000	Сдвиг
	0,0100	0,00001100	Сдвиг
	0,0010	0,00000110	Сдвиг
	0,0001	0,00000110 0,00110000 0,00110110	Сложение
		0,00011011	Сдвиг

Получили псевдопроизведение: 0,00011011

3.3.3 Произведём коррекцию (прибавим к псевдопроизведению A_дк):

0,00011011

А_дк= 0,01110000

0,10001011

3.3.4 Присвоение произведению знака:

(A*B)_дк=1,10001011

(A*B)_пк=1,01110101

A*B = (9)*(-13) = -117 = -1110101₂

3.4 Сомножители отрицательные (A<0, B<0)

 A = -9= -1001₂, А_пк = 1,1001, А_дк = 1,0111

 B =-13=-1101₂, В_пк = 1,1101, В_дк = 0,0011

3.4.1 Определим знак произведения: 1 + 1 = 0

3.4.2 Перемножим модули сомножителей:

Таблица 4

Множитель	Множитель	Сумматор	Пояснения
0,0011	0,0111	0,00000000 0,00110000 0,00110000	Сложение
		0,00011000	Сдвиг
	0,0011	0,00011000 0,00110000 0,01001000	Сложение
		0,00100100	Сдвиг
	0,0001	0,00100100 0,00110000 0,01010100	Сложение
		0,00101010	Сдвиг
	0,0000	0,00010101	Сдвиг

Получили псевдопроизведение: 0,00010101

3.4.3 Произведём коррекцию (прибавим к псевдопроизведению B_пк, а затем A_пк):

0,00010101

В_пк= 0,11010000

0,11100101

A_пк= 0,10010000

0,01110101

3.4.4 Присвоение произведению знака:

(A*B)_дк=0,01110101

(A*B)_пк=0,01110101

A*B = (-9)*(-13) = 117 = -1110101₂

4 Выбор и описание структурной схемы операционного автомата (ОА)

 

ОА должен содержать:

-      регистры RG1, RG2 для приема мантисс операндов с ШИВх;

-      регистр RG3  и счетчик CT1 для приема характеристик с ШИВх;

-      регистр RG4 для записи и хранения результата и частных сумм;

-      комбинационные сумматоры SM;

-      счетчик CT2 для подсчета тактов умножения;

-      три сумматора по модулю 2 для получения обратного кода множимого и определения ПРС;

-      триггер T1 для хранения знака результата;

-      схему конъюнкции;

-      триггер T2 для фиксации ПРС;

-      усилитель-формирователь для выдачи результата на ШИВых.

Операнды поступают в операционный автомат по 32-разрядной шине ШИВх. Перед началом умножения необходимо обнулить регистр частных сумм RG4, так как именно с него поступает информация на плечо A в SM, в счетчик CT2 необходимо занести “001001”, а триггер T1 сбросить. Операнды поступают в дополнительном коде. Сначала мантисса множителя записывается в RG1 и RG2, а его характеристика в RG3 и CT1. Мантисса первого операнда преобразуется в ДК с помощью схемы сложения по модулю 2 и сумматора и заносится в RG4. Затем записываются мантисса и характеристика множимого в RG2 и CT1 соответственно. После анализа знаков операндов произведем коррекцию, если это необходимо. Если знаковый разряд множимого (p2) равен 0, то обнуляем RG4. Если знаковый разряд множителя (p1) равен 1, то в RG4 заносим информацию с плеча S сумматора. После проведения коррекции начинается процесс получения псевдопроизведения. В процессе умножения происходят сдвиги регистров RG1 и RG4, а также увеличение счетчика CT2. Кроме того производится анализ младшего разряда RG1 (p4). Если он равен 1 тогда в RG4 заносим информацию с плеча S сумматора. Получение псевдопроизведения происходит до тех пор пока 5-й разряд в счетчике CT2 не окажется равным “1”. Далее производится анализ старшего разряда мантиссы результата. Если он равен “0” – требуется нормализация. Нормализация осуществляется путем сдвига RG4 влево и уменьшеня счетчика CT1. Характеристика произведения получается обычным сложением характеристик операндов, причем старший разряд характеристики у множителя подается инверсным на плечо сумматора A. Перед выдачей результата на ШИВых содержимое RG3, T1 и информация с плеча S сумматора SM2 подается на усилитель-формирователь.

Таким образом, для выполнения операции умножения из управляющего автомата в операционный автомат необходимо подать управляющие сигналы, реализующие следующие микрооперации:

y1 - запись в RG1,

запись в RG3,

сброс T1,

занесение “001001” в CT2;

y2 - запись в RG2,

запись в CT1,

разрешить запись в T1;

y3 - обнуление RG4;

y4 - запись в RG4;

y5 - CT2:=CT2+1,

сдвинуть вправо RG1:=0.R1(RG1),

сдвинуть вправо RG4:=0.R1(RG4);

y6 - SM_p=1 – подача “1” на вход переноса сумматора,

управление совокупностью схем сложения по модулю 2;

y7 - CT1:=CT1-1,

сдвиг влево RG4:=L1(RG4).0;

y8 - управление выдачей на ШИВых;

Из операционного автомата в управляющий автомат необходимо передать осведомительные сигналы о состоянии устройств операционного автомата, определяемые списком следующих логических условий.

Х - проверка наличия операндов на ШИВх,

p1 - знак операнда в RG1;

p2 - знак операнда в RG2;

p3 - проверка на наличие нулевого операнда в RG2;

p4 - проверка очередной цифры множителя;

p5 - проверка условия выхода из цикла;

p6 - проверка результата на нормализованность;

p7 - проверка условия ПРС;

Z - проверка возможности выдачи по ШИВых.

Таким образом, управляющий МПА должен вырабатывать 8 управляющих сигналов и посылать их в ОА в нужные такты машинного времени в соответствии с алгоритмом выполнения операции сложения, ориентируясь на 9 осведомительных сигналов, поступающих из ОА, структурная схема которой представлена на рисунке 1.