Навигация
Получение логических выражений для функций возбуждения RS-триггеров
8.6 Получение логических выражений для функций возбуждения RS-триггеров.
Далее составляем прямую структурную таблицу переходов и выходов автомата Мура (таблица 19) и по известному правилу формируем логические выражения для функций возбуждения.
Таблица 19. Прямая структурная таблица переходов и выходов автомата Мура.
| Исходное состояние bm | Выходные сигналы | Код bm | Состояние перехода bs | Код Bs | Входной сигнал | Функции возбуждения D-триггеров |
| b0 | - | 0000 | b0 b1 | 0000 0001 | X1 X1 | S4 |
| b1 | y1,y2,y3 | 0001 | b2 b12 | 0011 1011 | X2 X2 | S3 S1S3 |
| b2 | y4,y6 | 0011 | b3 b4 | 0010 0110 | X1 X1 | R4 S2R4 |
| b3 | - | 0010 | b3 b4 | 0010 0110 | X1 X1 | S2 |
| b4 | y2 | 0110 | b5 b6 b7 b8 b12 | 0100 0101 0111 1100 1011 | X2X3 X2X3X4 X2X3X4X5 X2X3X4X5 X2 | R3 R3S4 S4 S1R3 S1R2S4 |
| b5 | y3 | 0100 | b6 b7 b8 | 0101 0111 1100 | X4 X4X5 X4X5 | S4 S3S4 S1 |
| b6 | y4,y6 | 0101 | b7 b8 | 0111 1100 | X5 X5 | S3 S1R4 |
| b7 | y4 | 0111 | b8 | 1100 | 1 | S1R3R4 |
| b8 | y5 | 1100 | b0 b7 b8 b9 b10 b11 | 0000 0111 1100 1000 1110 1010 | X6X7X8 X6X5 X6X5 X6X7 X6X7X8X9 X6X7X8X9 | R1R2 R1S3S4 R2 S3 R2S3 |
| b9 | y7 | 1000 | b0 b9 b10 b11 | 0000 1000 1110 1010 | X7X8 X7 X7X8X9 X7X8X9 | R1 S2S3 S3 |
| b10 | - | 1110 | b10 b11 | 1110 1010 | X9 X9 | R2 |
| b11 | y8 | 1010 | b0 | 0000 | 1 | R1R3 |
| b12 | y1,y3 | 1011 | b10 b11 | 1110 1010 | X9 X9 | R2S4 R4 |
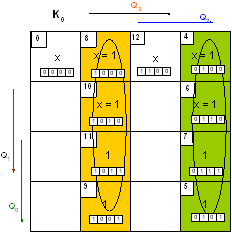
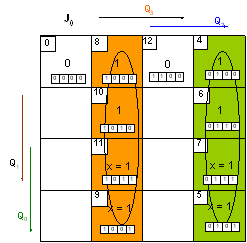
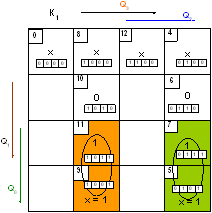
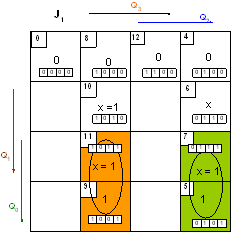
Так как мы изменили используемые элементы памяти, то у нас изменятся логические выражения для функций их возбуждения, а логические выражения для функций выходов не изменятся.
S1= b1x2 v b4x2x3x4x5 v b4x2 v b5x4x5 v b6x5 v b7
S2= b2x1 v b3x1 v b9x7x8x9 v b12x9
S3=b1 v b5x4x5 v b6x5 v b8x6x5 v b8x6x7x8 v b9x7x8
S4= b0x1 v b4x2x3x4 v b4x2x3x4x5 v b4x2 v b5x4 v b5x4x5 v b8x6x5
R1= b8x6x7x8 v b8x6x5 v b9x7x8 v b11
R2= b4x2 v b8x6x7x8 v b8x6x7 v b8x6x7x8x9 v b10x9
R3= b4x2x3 v b4x2x3x4 v b4x2x3x4x5 v b7 b11
R4= b6x5 v b2 v b7 vb12
Упростив и выделив общие части получаем:
d=b4x2
q=b4x2
e=qx3
r=x4x5
f=b5r
g=b6x5
s=b8x6
m=x7x8
h=sm
i=b8x6x5
j=b8x6x7x8
k=b9x7x8
n=x4x5
p=b2 v b7
S1= b1x2 v en v d v b5n v g v b7
S2= x1(b2 v b3) v x9(k v b12)
S3= b1 v f v b6x5 v i v j v k
S4= b0x1 v e(x4 v r) v d v b5x4
R1= h v i v b9m v b11
R2= d v h v sx7 v x9(j v b10)
R3= qx3 v e(x4 v n) v b7 v b11
R4= g v p v b12
y1= b1 v b12
y2= b1 v b4
y3= b1 v b5 v b12
y4= p v b6
y5= b8
y6= b2 v b6
y7= b9
y8=b11
С использованием в качестве элементов памяти RS-триггеров, цена комбинационной схемы по Квайну для автомата Мура равна С =114 причем в схеме предполагается использовать 4-входовой дешифратор.
Унитарный способ кодирования не может быть использован, так как n намного меньше N , где N наибольшее число ЭП (N=13), а n наименьшее число ЭП (n=log2 16).
Способ кодирование для счетчика так же не может быть использован, так как в данном графе содержится большое количество нестандартных переходов.
Сравнивая относительно аппаратурных затрат варианты построения автомата Мура на RS и D-триггерах можно убедиться что цена логических выражений для функций возбуждения ЭП отличается не на много: для RS цена - 114, для D цена - 109.
Сравнение вариантов построения управляющего автомата по модели Мили и модели Мура показывает, что модель Мура дает комбинационную схему большей сложности. Однако следует обратить внимание на то, что комбинационная схема, реализующая функции выходов автомата Мура, чрезвычайно проста (ее цена для схемы использующей D-триггеры, С=11).
9 Построение функциональной схемы микропрограммного управляющего автомата
Сравнивая построения автомата на основе модели Мура и Мили, видно, что построение автомата по модели Мили требует меньше аппаратурных затрат, чем построение автомата по модели Мура. Модель Мили на D-триггерах имеет цену по Квайну 59, на RS-триггерах цена также составляет 59, на T-триггерах цена составляет 61, а на счётчике цена составляет 57.
Наиболее оптимальной по аппаратурным затратам и стоимости является модель Мили на счётчике, поэтому функциональная схема МПА будет строиться именно для этой модели.
На рисунке 6 приведена функциональная схема проектируемого МПА, управляющего операцией умножения двоичных чисел с ПЗ в ДК с простой коррекцией. Функциональная схема построена в основном логическом базисе И, ИЛИ, НЕ в полном соответствии с приведенной для модели Мили системой логических уравнений для функций возбуждения элементов памяти.
Заключение
В ходе выполнения курсовой работы была разработана функциональная схема МПА, управляющего операцией умножения двоичных чисел в форме с плавающей запятой и характеристикой в дополнительном коде первым способом с простой коррекцией.
При синтезе МПА была рассмотрена модель Мили и модель Мура. В результате проделанной работы оказалось, что наименьшие аппаратурные затраты даёт модель Мили с использованием счётчика в качестве элементов памяти.
Библиографический список
1. Курс лекций по дисциплине “Дискретная математика”.
2. Т.Р.Фадеева. Синтез Микропрограммного управляющего автомата. Методические указания к курсовой работе. Киров, 1989 год.
3. Б.М.Каган. Электронные вычислительные машины и системы. М.: Энергоатомиздат, 1985.
4. Курс лекций по дисциплине “Теория автоматов”.
5. Лысиков Б.Г. Арифметические и логические основы цифровых автоматов. Минск: ВМ, 1980.
Перечень сокращений
ГСА - граф-схема алгоритма,
УА - управляющий автомат,
ОА - операционный автомат,
ПРС - переполнение разрядной сетки,
ФЗ - фиксированная запятая,
ДК - дополнительный код,
МПА - микропрограммный аппарат,
МК - микрокоманда,
МО - микрооперация.
Похожие работы
... покажет уровень полученных нами знаний по курсу «Прикладная теория цифровых автоматов». Задание Выполнить синтез управляющего автомата операции умножения младшими разрядами вперед со сдвигом множимого над числами в форме с фиксированной точкой в формате {1,8}в прямом коде двоичной системы счисления. Разработать микропрограмму и выполнить синтез управляющего автомата используя синхронный ...
... начинается фаза интерпретации команды. В зависимости от команды эта фаза может представлять собой, например, извлечение из памяти константы, необходимой для выполнения команды или извлечение из памяти номера регистра. В конце этой фазы процессор готов к выполнению команды. На этом начинается фаза выполнения. Фаза извлечения данных из памяти присутствует у команды занесения данных в аккумулятор, в ...
... входов для каждого триггера: МДНФ счётчика: ; ; ; . · Синтезируем счётчик. Структурную схему: Принципиальную схему: Временные диаграммы счётчика: Синтез дешифратора Мы должны получить неполный ...
... состоянии am. Рассмотренные выше абстрактные автоматы можно разделить на: 1) полностью определенные и частичные; 2) детерминированные и вероятностные; 3) синхронные и асинхронные; Полностью определенным называется абстрактный цифровой автомат, у которого функция переходов и функция выходов определены для всех пар ( ai, zj). Частичным называется абстрактный автомат, у которого функция ...


0 комментариев