Основные определения

5.1.2. Основные определения

Термин “моделирование” имеет в литературе много различных толкований. Наиболее приемлемым на взгляд многих авторов является такое определение:

моделирование есть метод изучения системы путем ее замены более удобной для экспериментальных исследований системой, называемой моделью и сохраняющей наиболее существенные черты оригинала.

И как дополнение можно использовать следующее определение:

моделирование есть общий метод изучения объекта путем исследования замещающей его модели с переносом получаемой информации на изучаемый объект.

Отправной точкой при построении модели технической системы следует считать описание.

Описание - совокупность сведений об исследуемой системе и условиях, при которых необходимо провести исследования.

Описание представляется в виде:

-схем;

-текстов;

-формул;

-таблиц экспериментальных данных;

-характеристик внешних воздействий и окружающей систему внешней среды.

Описание задает предполагаемый алгоритм работы системы и может формально рассматриваться как некоторая функция внешних воздействий.

В качестве примера можно без достаточной детализации рассмотреть описание модели системы распознавания речи.

Здесь, во-первых, исходя из того, что описание - это сведения о системе и условиях ее применения, нужно более точно определить систему распознавания речи, Например:

“Система распознавания речевых команд управления подъемом стекол автомобиля в процессе его эксплуатации”.

Для такой системы описание модели должно включать:

-схему речевого аппарата человека и теоретические положения речеобразования;

-описание условий речевого управления (шумы двигателя, шумы окружающей среды и т.д.);

-характеристики микрофона, как датчика сигналов, воспринимающего команду (зависимость выходных сигналов от звукового давления во всем диапазоне частот, например, в виде таблиц);

-характеристики сигналов управления (мощность, направленность, удаленность от микрофона);

-характеристики канала приема электрических сигналов на входе преобразователя “аналог-цифра” компьютера (чувствительность, дискретность, точность и т.п.);

-математические зависимости, применяемые для обработки принятого сигнала с целью получения признаков распознавания и классификации;

-способ преобразования результатов распознавания в команды управления;

-характеристики канала передачи команд управления;

-требования к величинам сигналов управления двигателями подъема стекол. и т.д. и т.п. )

Модель воспроизводит описание системы с большими или меньшими упрощениями, зависящими от намерений исследователя, возможностей вычислительных средств, имеющихся в его распоряжении и времени, отпускаемого на проведение испытаний.

При этом должен достигаться разумный компромисс между точностью воспроизведения моделью характеристик системы и сложностью необходимых для этого мер и средств.

Другими словами (основываясь на рассмотрении описания системы как функции внешних воздействий) , при моделировании производится аппроксимация функции-описания более простой и удобной для машинного представления функцией-моделью .

Аналогия между построением модели и аппроксимацией позволяет использовать для наглядности представлений аппроксимацию функции w(x) на некотором отрезке [a,b] линейной комбинацией

Здесь - модель функции-описания w(x) характеризуется

n параметрами (числовыми коэффициентами a_i );

j _i (x) - некоторые возможные простые функции, заданные на том же отрезке [a,b].

Теперь, исходя из характеристики модели (см. выше положение о том, что модель воспроизводит систему с упрощениями), варьируя параметрами a_i , необходимо получить наилучшее или удовлетворяющее исследователя (в некотором смысле) приближение функции-модели к функции-описанию.

Обычно для оценки точности описания и модели пользуются более удобной для вычисления мерой

где Q_w - скалярный показатель, который намереваются получить при исследовании системы (например, производительность, надежность, пропускная способность); Q_m - скалярный показатель, соответствующий Q_w, но полученный при анализе модели m.

При этом описание w(x) и модель m(x) отождествлены с векторами w и m некоторого многомерного пространства.

Если при этом описание полностью характеризует систему и ее состояния и существует некоторое взаимно-однозначное преобразование

и

то модель и система (в крайнем случае ее описание) изоморфны.

При выполнении только второго соотношения, то есть при отсутствии обратного преобразования, имеем дело с гомоморфностью.

Л Е К Ц И Я 5.2

Моделирование сложных систем и применение моделей

5.2.1. Принципы построения модели сложной системы

а) Принцип декомпозиции

Прежде всего исходим из того очевидного положения, что сложные системы можно разбить на подсистемы и элементы с иерархической структурой связей. Тогда каждая подсистема, решая конкретную задачу, обеспечивает тем самым достижение общей цели.

С этих позиций, к особенностям сложной системы следует отнести такие:

1)Сложную систему можно расчленить на конечное число подсистем, а каждую подсистему, в свою очередь, - на конечное число более простых субподсистем до тех пор, пока не получим элементы системы ( под элементами системы следует понимать объекты, которые в условиях данной задачи не подлежат расчленению на части) .

2)Элементы сложной системы функционируют во взаимодействии друг с другом.

3)Свойства сложной системы определяются не только свойствами отдельных элементов, но и характером взаимодействия между ними.

На практике стремятся расчленить сложную систему на такую совокупность подсистем, которая наилучшим образом отражала бы работу и функциональное взаимодействие ее элементов. В этом случае и строгое физико-математическое описание становится более доступным.

Использование принципа декомпозиции систем на подсистемы, подсистем на элементы позволяет создать модель сложной системы путем разработки для простых физически элементов их математическое описание и соответствующий алгоритм.

Практическая реализация этого принципа предполагает, что специалисты, изучающие процессы в каждом конкретном элементе, способны на основе экспериментальных и теоретических исследований разработать модели всех элементов и достичь при этом точности, которая необходима для оценки характеристик работоспособности каждого из этих элементов в условиях штатной эксплуатации.

Например, выделив в качестве отдельного элемента системы двигатель постоянного тока, даем возможность специалисту формировать его описание. Так из теории систем автоматического регулирования для такого двигателя описанием является система дифференциальных уравнений

или после упрощения и преобразований

,

где ,

Таким образом субблоки, блоки, элементы сложной системы или удается описать математически с достаточной степенью точности для расчета их текущих состояний, или в результате специальных экспериментальных исследований получить совокупность числовых данных для описания указанных состояний. Эти числовые данные могут быть как непосредственно использованы при компьютерной реализации соответствующих блоков в виде таблиц, описывающих реакцию этих блоков на входные воздействия, так и в виде заменяющих упомянутые таблицы аппроксимирующих их зависимостей. И в том и в другом случаях программирование не вызывает трудностей.

Так или иначе декомпозиция системы, о которой идет речь, дает возможность специалистам создать программно реализуемые алгоритмы функционирования блоков, субблоков, элементов.

Отсюда совокупность моделирующих алгоритмов блоков, субблоков, элементов, разработанных указанным способом, с учетом их взаимодействия определяют алгоритм модели всей системы в целом.

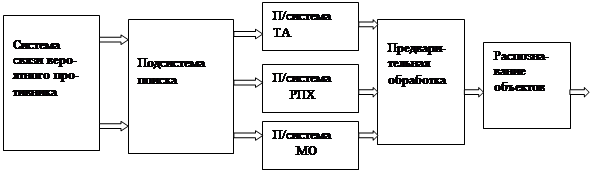
Примерами декомпозиции при создании модели системы распознавания заболеваний внутренних органов человека могут быть варианты разбиения ее на элементы и блоки компьютерной системы, построенной на основе ультразвуковой медицинской диагностики. Структурная схема одного такого варианта при достаточно поверхностной декомпозиции представлена на рис. 5.2.1.

Модель отражающих Модель ультразву-

свойств внутренне- кового локатора,

го органа человека в являющегося ос- ультразвуковом новным элементом

диапазоне волн аппарата УЗИ

Модель алгоритма

обработки изображе-

ний внутреннего ор-

гана

Модель алгоритма

анализа и принятия

решения

Рис 5.2.1. Структурная схема варианта декомпозиции системы распознавания

Более детальная декомпозиция позволяет представленные блоки расчленить на субблоки и элементы. Так , например, могут быть детализированы первые два из блоков рассмотренной схемы (Рис.5.2.2).

Точно также могут быть подвергнуты декомпозиции и другие модули структурной схемы, приведенной на рис.5.2.1. В результате появляется возможность для узких специалистов на основе физико-математического описания разработать алгоритмы их и затем комплексировать в общий алгоритм модели системы.

а) Принцип допустимых упрощений

В большинстве случаев, однако, общий алгоритм модели, полученный в результате декомпозиции системы, разработки специалистами алгоритмов элементов и их связей и последующего объединения, является

Модуль описания Модуль описания

геометрической возможных поло-

формы внутрен- жений потологи-

него органа ческих образо-

ваний в органе

Модуль описания Модуль описания

положений функцио- геометрических

нальных элементов характеристик

внутреннего органа потологических

образований

Модуль выбора

условий наблюде-

ния внутреннего

органа (сечение)

Модуль описания

звукодинамичес-

ких свойств се-

чения органа

Модуль описания Модуль описания Модуль описания

звукодинамичес- звукодинамичес- звукодинамичес-

ких свойств па- ких свойств каж- ких свойств па-

тологических дого из функцио- ренхимы внутрен-

образований нальных элементов него органа

Модуль формирования ультазвуково-

го изображения сечения органа

на модель алгоритма обработки изображений

Рис.5.2.2. Структурная схема декомпозиции модели отражающих свойств и ультразвукового локатора

только исходным и его еще нельзя положить в основу создания рабочей модели системы. Это определяется его громоздкостью, а также плохой согласованность с вычислительными ресурсами и с требованиями к модели системы.

Такие возможные недостатки исходного алгоритма модели вытекают из различия целей моделирования отдельных элементов и сложной системы в целом.

Причина различия целей состоит в том, что специалисты, разрабатывающие алгоритмы элементов, стремятся к тому, чтобы отразить характеристики этих элементов с максимальной точностью. В результате алгоритмы моделей элементов могут оказаться достаточно сложными, а в итоге

-непомерно возрастает время счета одной реализации функционирования системы в целом;

-уменьшается общее число модельных экспериментов (реализаций) при общем ограничении времени на испытание сложной системы.

И это при том, что всегда существуют более простые реализации элементов по сравнению с предложенными “сходу”. К тому же с точки зрения влияния на конечную точность моделирования системы вклады отдельных элементов могут оказаться несущественными, а значит сами описания алгоритмов их функционирования могут допускать упрощения.

Поэтому модель системы в целом должна строиться на основе компромисса между ожидаемой точностью оценок конечного показателя и сложностью самой модели.

Отсюда путь к созданию рабочей модели системы - поиск компромиссных решений. В основе его лежит анализ допустимых упрощений как исходных алгоритмов моделей элементов, так и алгоритмов их взаимодействия.

При создании рабочей модели системы (разработке алгоритма модели) методики анализа возможных упрощений бывают самыми разными, но смысловое содержание их состоит в том, чтобы обеспечить системные расчеты в отведенное время и достичь при этом заданной точности конечного показателя (например, эффективности для систем распознавания). Естественно, что указанный анализ, направленный на исключение, замену отдельных блоков и субблоков или их корректировку должен предполагать:

-более углубленное аналитическое изучение и представление работы физического аналога;

-экспериментальные исследования физического аналога.

Решения по упрощению многообразны. Все они специфичны и не поддаются обобщению. При этом наиболее конкретная рекомендация по замене может быть дана лишь в отношении блоков, осуществляющих воздействие на исследуемую часть системы. Только в этой ситуации блоки можно однозначно заменить упрощенным эквивалентом, не зависящим от указанной исследуемой части системы. Само собой разумеется, что если при заменах и корректировках не нарушается функциональное взаимодействие блоков и субблоков, то схема сопряжения их в общей модели остается без изменений.

При заменах блоков упрощенным эквивалентом отказываются от точного описания

-либо на основе отдельных исследований на самостоятельной модели (говорят: ”частной” модели) воздействий, данного блока на систему и выбора в качестве замены нового блока формирующего реализации наихудшего воздействия;

-либо при достаточно большом числе факторов, определяющих воздействие, выбором в качестве замены нового блока, формирующего случайное воздействие с заданными характеристиками.

Если, например, в состав некоторой сложной системы входит автоматический электронный измеритель некоторой величины, используемой блоками этой системы, то приходится иметь дело с неизбежными ошибками измерений. Причины ошибок здесь - наличие электронных шумов, вызываемых:

-неравномерной эмиссией электронов (так называемый “дробовой шум) в электровакуумных приборах;

-неравномерностью процессов генерации и рекомбинации носителей тока в полупроводниковых приборах.

При построении модели указанного измерителя возможны:

1)Строгое физико-математическое описание указанных неравномерностей движения носителей тока и их влияния на измеряемую величину ("модель с точностью до носителя").

2)Экспериментальная оценка максимальной ошибки измерения интересующего параметра и замены точного блока всего лишь имитатором постоянной величины максимально возможной ошибки, добавляемой к измерениям.

3)Экспериментальные статистические исследования ошибок измерителя, получение закона распределения вероятностей ошибок и замена точного блока на блок генерации случайных ошибок с заданным законом распределения, добавляемых к “чистым” измерениям.

В технических приложениях моделирования ни "точность до носителя", ни имитация максимальных ошибок не являются удовлетворительным решением. Третий подход к решению задачи встречается наиболее часто. Это связано, особенно в электронике, с наличием большого числа случайных воздействий. Это и каналы связи со случайными шумами. Это и ошибки измерений, носящие случайный характер. Это и точности изготовления деталей и т.д. и т.п.

Отсюда следует, что при соответствующих заменах блоков каждый эксперимент на системной модели должен носить случайный характер.

Похожие работы

История систем распознавания образов

Скачать

31987

0

4

... именно по этой причине современное распознавание образов само питается идеями этих дисциплин. Не претендуя на полноту (а на нее в небольшом эссе претендовать невозможно) опишем историю распознавания образов, ключевые идеи [5, c. 107]. 2. Определения Прежде, чем приступить к основным методам распознавания образов, приведем несколько необходимых определений. Распознавание образов (объектов, ...

Автоматизированные Системы Обработки Информации

Скачать

115369

7

12

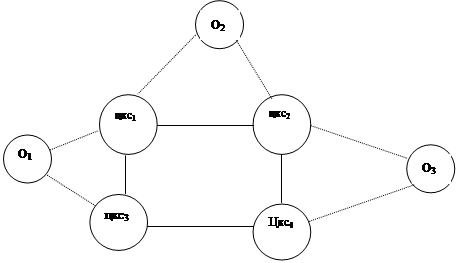
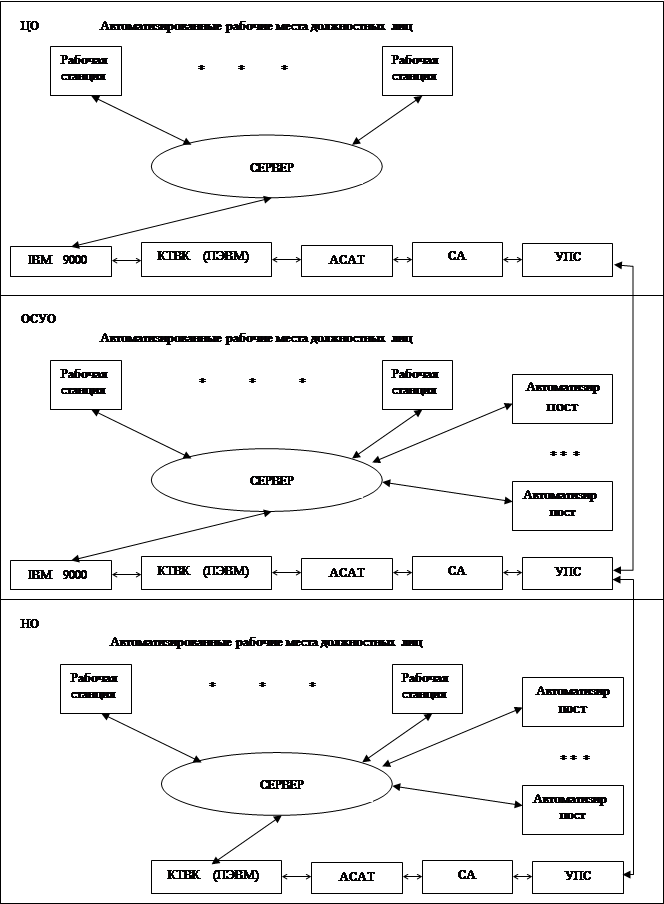
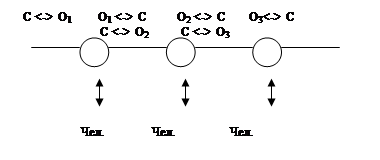
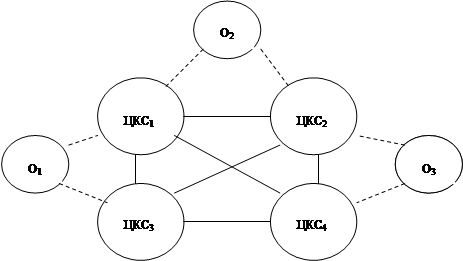
... звеньях основной акцент делается на получение и передачу информации в вышестоящие органы. В вышестоящих органах возрастает число задач, связанных с планированием, управлением и обработкой информации. В каждом звене имеется своя автоматизированная система, которая в свою очередь может иметь несколько уровней. Так специальная система состоит из объектов центрального звена, объектов среднего уровня ...

Афизикальные принципы психического отражения и их моделирование в технических системах

Скачать

83630

0

0

... свойства), которые сами являются результатами или компонентами промежуточных стадий этого процесса. 3. Афизикальные принципы формопорождения в процессах психического отражения Проведенный анализ методологических оснований естественнонаучного исследования непосредственно-чувственного отражения, а также способов его моделирования в технических системах привел нас к выводу о том, что в психологии, ...

Использование нейросетей для построения системы распознавания речи

Скачать

33014

0

5

... , но только для обычных последовательных вычислительных машин. А какие же ещё машины смогут решить все вышеперечисленные проблемы? – спросите Вы. Совершенно верно, это нейросети. 2. Возможность использования нейросетей для построения системы распознавания речи Классификация - это одна из «любимых» для нейросетей задач. Причем нейросеть может выполнять классификацию даже при обучении без ...