Fm 3Fm f
X(t)
Восстановление и демонстрация цифровых изображений
Свойства системы зрения человека
Некоторые замечания о сокращении избыточности изображений
Схемы сокращения избыточности изображений с обработкой в пространственной области
Схемы сокращения избыточности изображений с обработкой в области преобразований
Другие аспекты задачи сокращения избыточности
Основные методы повышения резкости изображений
Повышение резкости изображения «вслепую» и методом уравнивания энергетических спектров
Замечания о восстановлении изображений в яркостной и плотностной областях
Повышение резкости изображений с характеристиками
Воспроизведение изображений по проекциям
Методы воспроизведения изображений
Повышение качества изображений
Навигация
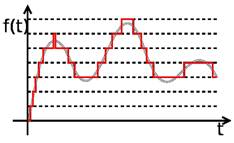
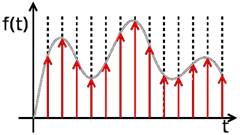
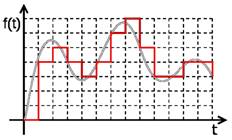
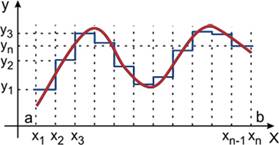
Дискретизация и квантование изображений
Дискретизация и квантование изображений
133819
знаков
3
таблицы
0
изображений
ИСТОРИЧЕСКИЙ ОЧЕРК.
Еще с середины 40-ых годов , специалисты по радиоэлектроники начали задумываться над возможностью применения специализированных цифровых устройств для решения разнообразных задач ,связанных с обработкой сигналов . Нечего и говорить , что в то время выводы не были благоприятными . С точки зрения стоимости, размеров и надежности предпочтение следовало отдать аналоговой фильтрации и аналоговым методам спектрального анализа . В 50-ых годах теория управления , частично основанная на работе Гуревича ( 1945 г.) , уже утвердилась как самостоятельное научное направление ; были глубоко изучены принципы дискретизации колебаний и возникающие при этом спектральные эффекты , а математический аппарат теории z-преобразования , существовавший еще со времен Лапласа , начал находить применение в радиоэлектроники и смежных дисциплинах . Однако достигнутый уровень развития техники позволял получить практические результаты только в задачах управления медленными процессами и обработке низкочастотных сейсмических сигналов . К середине 60-ых годов были оценены потенциальные возможности интегральных микросхем , что позволило представить полную систему обработки сигналов , для которых наилучшая техническая реализация была бы именно цифровой .
Первый крупный вклад в теорию цифровой обработки сигналов , касающийся анализа и синтеза цифровых фильтров , был сделан Кайзером ( фирма Bell ) ; он показал , как можно рассчитывать цифровые фильтры с нужными характеристиками , используя билинейное преобразование . Примерно тогда же ( 1965 г.) появилась статья Кули и Тьюки о быстром методе вычисления дискретного преобразования Фурье , давшая мощный толчек развитию этого нового технического направления . Позже метод был развит и стал широко известен как быстрое преобразование Фурье ( БПФ ) . Ценность этого метода заключается в сокращении времени вычисления дискретного преобразования Фурье ( на один-два порядка для большинства практических задач ). Опубликование статьи Кули и Тьюки ускорило развитие строгой и достаточно полной теории цифровой фильтрации . Важнейшее значение метода БПФ состояло в том , что он наглядно продемонстрировал , насколько цифровые методы при спектральном анализе могут оказаться экономичнее аналоговых . После создания метода БПФ интенсивность исследований в области цифровой фильтрации резко возросла , и в настоящее время цифровые методы широко используются для спектрального анализа самых разнообразных сигналов , начиная с низкочастотных колебаний в сейсмологии и звуковых колебаний в гидрологии и при анализе речи и кончая видеосигналами в радиолокации .
Первой попыткой исчерпывающего изложения теории цифровой обработки сигналов была книга Гоулда и Рэйдера ( 1969 г.) . Эту книгу применяли в качестве учебного пособия для аспирантов, и как руководство для инженеров ,работающих в промышленности . Естественно , что книга не могла удовлетворить и тех и других . Не нужно доказывать , что хорошее учебное пособие может быть составленно только на основе курса , читавшегося в течении по крайней мере несколько лет , и подходящего набора задач .
ПРИЧИНЫ ВНЕДРЕНИЯ ЦОС В
ЭЛЕКТРОСВЯЗЬ.
1. Сложность ( нередко невозможность ) решения некоторых задач аналоговым методом .
2. Прогресс в развитии электроники ( создание высокоскоростных многоразрядных АЦП , разработка сигнальных процессоров ) .
3. ЦОС позволяет реализовать универсальные модемы , в которых изменением программы осуществляется переход с одного вида сигнала на другой ( т.е. с одной модуляции на другую ).
4. ЦОС позволяет строить адаптивные радиоприемные устройства, работающие во все усложняющейся электромагнитной обстановке ( т.е. спектр постоянно загружается сигналами ) .
5. Простота , автоматически сменных , алгоритмов ЦОС и высокая точность их реализации .
6. ЦОС позволяет реализовать более сложные алгоритмы радио приема ( разнесенный прием , компенсация и подавление сосредоточенных помех и прием в целом ) .
7. При использование ЦОС значительно меньше влияет разброс параметров и действие дестабилизирующих факторов.
8. Высокая интеграция цифровых микросхем позволяет реализовать очень сложные алгоритмы приема сигналов , сохраняя приемлемый объем и стоимость аппаратуры .
9. Цифровая аппаратура легко поддается миниатюризации. Высокая технологичность и отсутствие регулировки понижает стоимость.
10.Проектирование цифровых устройств легче чем аналоговых и поддается автоматизации ( легко модулируются на ЭВМ ) .
11.ЦОС облегчает работу по созданию спецэфектов на ТВ ( работа режиссеров на теле-студии ) .
12.ЦОС позволяет существенно повысить качество изображения.
ПРОБЛЕМЫ РАЗВИТИЯ ЦОС .
1. Для ЦОС необходимо преобразовать аналоговый сигнал в цифровой ( требуется достаточно большой уровень сигнала - порядка 1в ) .
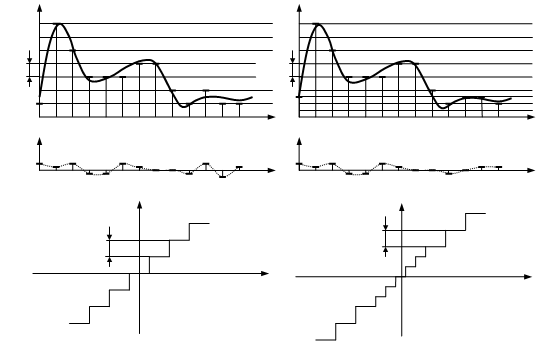
2. Преобразование аналогово сигнала в цифровой приводит к появлению погрешности дискретизации во времени и к погрешности квантования по уровню ( специфические погрешности ) .
3. Процесс обработки сигналов сопровождается погрешностями , вызванными округлениями результатов ( это приводит к ошибкам - шумам ) .
4.Требуется увеличение динамического диапазона и ширины спектра преобразуемых аналоговых сигналов ( т.к. каналы с ограниченной полосой пропускания и сложной помеховой обстановкой ) . Чтобы достигнуть возможности аналоговой техники нужно иметь динамический диапазон АЦП 120-130 дб с df=100 кГц . Таких АЦП пока нет . Реализуемый при df=100 кГц динамический диапазон АЦП 70-80 дб . Для широкополосных сигналов при df=100 Мгц динамический диапазон 6-24 дб .
5. Низкая скорость работы цифровых вычислительных устройств. (Сигнальные процессоры : КМ1813ВЕ11 , ТМS320.10 , ТМS320.20 , ТМS320.30 , ДSР5600 , ТМS320.50 .)
ТЕОРЕМА КОТЕЛЬНИКОВА .
Любой сигнал с ограниченным спектром ( бесконечный во времени ) однозначно определяется своими отсчетами , взятыми через интервал времени dt=1/2F т.е.
, где u(kDt)-аналоговая величина;
Эта теорема утверждает , что если сигнал f(t) имеет преобразование Фурье Sf(w) отличное от нуля при частотах меньших 2pFm . То в отсчетах сигнала f(kDt) взятых через интервал Dt=1/2Fm содержится вся информация о непрерывной функции f(t) . Из теоремы следует , что эти отсчеты содержат информацию о сигнале f(t) в любой момент времени . Однако частота отсчетов должна быть по крайней мере в два раза больше высшей частоты сигнала Fm .
Доказательство.:
Дан сигнал f(t) , его спектр : S(w)= при |w|<2pFm ,
0 , при |w|>2pFm.
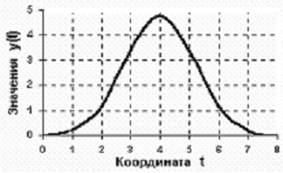
Представим некоторую реализацию сигнала f(t) и его спектр S(f):
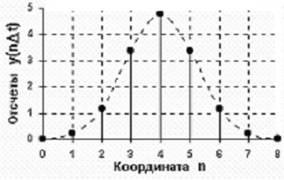
Если отсчеты сигнала брать с помощью бесконечно узких импульсов,расположенных в непосредственной близости друг от друга , мы однозначно определим любую функцию . Если интервал между импульсами увеличивать , то где-то мы начнем терять информацию о сигнале . Рассмотрим случай ,когда в качестве отсчетных импульсов используется периодическая последовательность импульсов длительностью t , повторяемых через Dt=1/2Fm . Временное и спектральное представление этих импульсов:
Спектр отсчетных импульсов можно записать в виде ряда Фурье , т.е. yD(t)=A1coslt+A2coslt+A3coslt+............ Процедуру взятия отсчетов удобно рассматривать как умножение функции f(t) на функцию yD(t) . Результирующий дискретизованный сигнал можно представить в виде суммы последовательностей импульсов ,амплитуды которых равны значению функции f(t) в момент отсчета , а спектр такого сигнала представляет собой периодически повторяющуюся функцию Sf(w) с периодом l ,т.е.мы наблюдаем изменение амплитуды импульсов отсчета по закону f(t) и соответственно имеем амплитудную модуляцию каждой гармоники спектра импульсов отсчета сигналa :
Для восстановления првоначального сигнала нам достаточно отфильтровать полученный сигнал ФНЧ с частотой среза расположенной в интервале от Fm до 1/Dt-Fm . Рассмотрим какова может быть наименьшая частота следования счетных D импульсов, что бы еще имелась возможность отфильтровать полезный сигнал. В случае , если 1/D t=2Fm мы еще имеем возможность отфильтровать полезный сигнал если же 1/Dt<2Fm ,то произойдет наложение спектральных составляющих и восстановление первоначального сигнала без ошибки станет невозможным. Следовательно , для восстановления сигнала ,полученные отсчетные импульсы необходимо подать на вход ФНЧ с частотой среза равной Fm. Реакция идеального ФНЧ на узкий импульс единичной амплитуду представляет собой функцию вида : y(t)=sin2pFt/2pFt
На вход фильтра мы подаем сумму импульсов с амплитудами равными f(kDt) Разложение сигнала f(t) в ряд Котельникова указывает на технический способ передачи непрерывной функции (сигнала) f(t)с ограниченным спектром путем передачи отсчетных импульсов ,который сводиться к следующему:
и со сдвигом один относительно другого на Dt=1/2Fm . Сигнал на выходе фильтра представляет собой сумму откликов ,т.е. Что соответствует ряду Котельникова .
Восстановление сигналов по его отсчетам .
1)взятие отсчета f(kDt) функции f(t) в моменты kDt ;
2)значение полученных отсчетов передаются на приемную сторону с использованием любогометода кодирования и модуляции ;
3)на приемной стороне вырабатываются короткие импульсы ,амплитуды которых пропорциональны принятым значениям отсчетов ;
4)полученные импульсы подаются на идеальный ФНЧ с частотой среза Fм . На выходе фильтра получается функция f '(t) , пропорциональная переданной функции f(t) . Идеальный ФНЧ с полосой пропускания Fм при действии на его вход единичного импульса d(t) дает на выходе напряжение ,соответствующее функции : y(t)=sin2p Fmt/2pFmt При восстановлении функции f(t) на вход фильтра подают короткие импульсы с амплитудами , соответствующими f(kDt) и с интервалами Dt. На выходе фильтра получается напряжение , соответствующее сумме откликов фильтра на каждый из импульсов . В моменты времени kDt функция f(t) восстанавливается совершенно точно , так как в этот момент только одна из отсчетных функций y(t-kDt) не равна нулю . В остальные моменты времени для точного восстановления необходимо суммировать бесконечное число отсчетных функций .
Ошибки восстановления сигнала по отсчетам Котельникова.
Как было отмечено выше , точное восстановление сигнала возможно только при строго ограниченном спектре сигнала и при использовании идеального ФНЧ .НА практике мы имеем дело с сигналами конечными во времени, т.е. бесконечным , теоретически , спектром и для восстановления используем реальные ФНЧ . Рассмотрим ошибки восстановления , вызванные реальностью сигнала (сигнал ограничен во времени , т.е. не ограничен по частоте ). Основная энергия сигнала сосредоточена в диапазоне частот до Fm и только малая доля будет выходить за Fm .
1)На основании т. Котельникова мы не можем восстановить спектральные составляющие , лежащие выше частоты Fm .
2)В спектре восстановленного сигнала появяться дополнительные составляющие , представляющие собой зеркальное отображение " вниз " по частоте спектральных составляющих сигнала относительно оси совпадающей с частотой среза идеального ФНЧ и равной Fm .Поясним
это на рисунке: фнч
S f(f) S1(f) S2(f) S3(f)
Похожие работы
... сигнала уровень квантования называют также глубиной дискретизации или битностью. Глубина дискретизации измеряется в битах и обозначает количество бит, выражающих амплитуду сигнала. Чем больше глубина дискретизации, тем точнее цифровой сигнал соответствует аналоговому. В случае однородного квантования глубину дискретизации называют также динамическим диапазоном и измеряют в децибелах (1 бит ≈ ...
... иметь дело с данными, имеющими конечный размер, – например, с массивами чисел конечного размера и ограниченной разрядности. Рассмотренная выше теорема дискретизации дает такую возможность. Количество информации, энтропия источника сообщений Для сравнения между собой различных источников сообщений необходимо ввести некоторую количественную меру, которая дала бы возможность объективно ...
... функций в виде зависимости их значений от определенных аргументов Δвремени, линейной или пространственной координаты и т.п.) при анализе и обработке данных широко используется математическое описание сигналов по аргументам, обратным аргументам динамического представления. Так, например, для времени обратным аргументом является частота. Возможность такого описания определяется тем, что любой ...
... рисунков в формате А0-А1 со скоростью 10-30 мм/с. Фотонаборный аппарат Фотонаборный аппарат можно увидеть только в солидной полиграфической фирме. Он отличается своим высоким разрешением. Для обработки информации фотонаборный аппарат оборудуется процессором растрового изображения RIP, который функционирует как интерпретатор PostScript в растровое изображение. В отличие от лазерного принтера в ...
0 комментариев