Fm 3Fm f

0  Fm 3Fm f

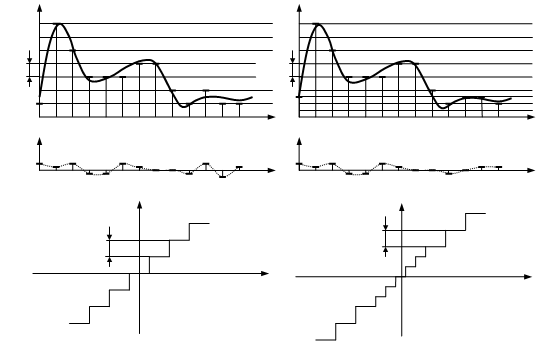
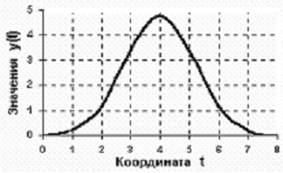
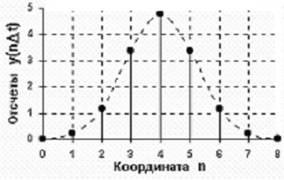
Огибающая спектральной плотности сигнала f(t) представляет собой функцию S1(f) . Спектр отсчетных импульсов SDf(f) представляет собой периодически повторяемую функцию S1(f) с периодом 2Fm . Идеальный ФНЧ с частотой среза Fm не пропускает составляющие основного сигнала и пропускает составляющие сектра амплитудно-модулируемой первой гармоники спектра отсчетных импульсов (2Fм) .

3)При восстановлении сигнала конечной длительности следует иметь ввиду что :

а) точность восстановления в средней части сигнала будет наибольшей, а по краям наименьшей;

б) в моменты , соответствующие отсчетам сигнал восстанавливается точно, а в средней части между отсчетными моментами ошибка максимальна

ВЫБОРКИ ИЗ АНАЛОГОВОГО СИГНАЛА.

Схема взятия выборки из аналогового сигнала.

1-Умножитель

2-Схема хранения УВХ

3-Квантователь

4-Преобразователь АЦП

5-Регистр

УВХ-устройство выборки и хранения. Перед умножителем стоит фильтр для уменьшения помех. Квантователь находит ближайший оцифрованный уровень. Устройство хранения дает время квантователю для принятия решения. Устройство хранения-конденсатор,окруженный ключами с большим сопротивлением ( т.е.RC-цепочкой с малой емкостью).Постоянная времени t стремится к единице, это переходный процесс в цепочке (т.е. конденсатор заряжается). За время Dt изменение сигнала мало,т.к. очень большое входное сопротивление преобразователя.Это и есть хранение. Преобразователь -преобразует вид кода (т.е. переводит его в бинарную систему счисления, за счет пороговых устройств). Регистр-считывает этот код, а за тем последовательно, побитно передает в линию.

ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ.

Квантование перидического сигнала.

W=2p/T

cosWT, cos2WT, ... , cosnWT.

n=3 n=Ґ

Много ли W нужно иметь и от чего это зависит (зависит от того насколько

гладкий сигнал).Если ширина спектра периодического сигнала конечно,

то он описывается конечным числом гармоник .N-кол-во отсчетов на один период.

ДПФ строго описывает периодический сигнал с конечным спектром ( если это не

соблюдается ,то появляется ошибка в представлении сигнала ДПФ ).

N-1

Cд(t)=е Ckd(t-kDt), где Т=NDt, Ck=C(kDt).

k=0

Ґ

т C(t)d(t-t)dt=C(t)-фильтрующее свойство d-функции.

-Ґ

Ґ

Cд(t)=е Cn*exp(j2npk/T) Пара преобразований Фурье

-Ґ

T

Cn=1/T тCд(t)exp(-j2npt/T)dt

0

NDt N-1

Сn=1/NDt т е Ckd(t-kDt)exp(-j2npt/T)dt={сжали ось времени symbol 120 \f "Symbol" \s 10xsymbol 61 \f "Symbol" \s 10=t/symbol 68 \f "Symbol" \s 10Dtsymbol 125 \f "Symbol" \s 10=

0 k=0

N N-1 N-1 N

=1/N т  е Ckd(x-k)exp(-j2pnx/n)dx=1/N е Ck  т d(x-k)exp(-j2npx/N)dx=

0 k=0 k=0 0

N-1

=1/N е Ckexp(-j2npk/N)

k=0

T=NDt

N-1

Cn=1/N е Ck exp(-j2npk/N) Пара дискретного преобразования Фурье

k=0

N-1

Ck= е Cn exp(jk2np/N)

0

Cn-комплексная гармоника, а N-кол-во отсчетов.

СВОЙСТВА ДИСКРЕТНОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ.

1. Линейность - если в цепи отклик на сумму воздействий равен сумме откликов.

Спектр суммы сигналов равен сумме спектров сигналов.

N-1

Ck= е Сxn exp(j2npk/N)

0 Выборки двух сигналов.

N-1

Uk= е Cyn exp(j2npk/N)

0

Zk=Ck+Uk , Линейность преобразования Фурье

Сzn=Cxn+Cyn ( для интегралов и сумм).

2. Для дискретного сигнала кол-во отсчетов спектра ( Сn) равно кол-ву

отсчетов сигнала.

3.Коэффициент (Со) дает постоянную составляющую.

N-1

Со=1/N е Ck ѕ это математическое ожидание.

k=0

4. Если N-четное ,то тогда

N-1 k

Cn/2=1/N е Ck(-1)

k=0

5. Если Ck - вещественные, то Cn ,расположенные симметрично

относительно Cn/2 образуют комплексно сопряженные пары.

N-1 N-1  +

C =1/N е Ck exp(-j2pk(N-n)/N)=1/N е Ck exp(j2kp/N)=Cn

N-n k=0 k=0

Отсчеты выше C повторяют спектр от Co до C .

N/2 N/2

Но мы не нарушаем теорему Котельникова, т.к. Сn комплексное число,

оно требует два числа для своего представления. Следовательно нужно

ровно N отсчетов ,как и по Котельникову ( N=2FT=T/Dt).

ЦАП и АЦП.

1 3 5

4

2 ЦАП АЦП 2

+5в +15в +5в

6 7 6

1.Стробирующий импульс ( аналоговая величина, соответствующая дис-

кретному слову).

2. N-разрядное дискретное слово (код).

3.Опорное аналоговое напряжение (определяет от какого сигнала ведется

счет т.е. служит для получения единиц измерения в дискретных долях).

4.Аналоговый сигнал.

5.Пуск (внешний сигнал - для конкретного момента времени будет получен

код).

6.Логическое питание.

7.Аналоговое питание.

Отдельные земли обеспечивают подавление импульсных помех ( т.е.возрастает

помехоустойчивость) по питанию.

Входные и выходные сигналы ЦАП и АЦП.

Сигналы ЦАП АЦП

аналоговый на выходе ; напряжение вход ; напряжение ; полярность ;

или ток ; полярность ; ве- величина ; ( есть однополярные

личина ( бывают одно- и двуполярные АЦП ) ;

и двуполярные ЦАП ) (2.5В , 5В , 10В , 10.24В , 20В)

(2.5В,5В,10В,10.24В,20В)

(1мА,1.2мА,1.5мА,2.5мА)

цифровое вход ; послед. или парал. выход ; последовательный

слово ( шина ) включение ; или параллельный ;

логические уровни :

ттл-5В ; эсл- -5В,-2.5В ;

кмоп-3В,15В ; источник

питания : анал.±15,±12В ;

дискр.+5В .

сигналы стробирующий импульс а) входной импульс начала

управления ( при завершении ввода преобразования.

слова , т.е. тактовый ввод) б) вых. “состояние”

( говорит , что на выходе

появился код )

Dt между сигналами а

и б - это врнмя , затрачи-

ваемое АЦП на преобра-

зование.

опорный эталонное напряжение , эталонное напряжение ;

относительно которого внешнее , внутреннее ;

ведется счет ; можно использавать перемен-

ное

При преобразовании мы можем получать прямой код Uвых. ( 0-10В ), или

двуполярный ( ± 10В ). При использовании ЦАП и АЦП необходимо обра-

тить внимание на используемый код ( т.к. они различны ).

Однополярные : как правило старший разряд обеспечивает 0,5 Uопор. ,

n

следующий разряд 0,25 Uопор. , ... , младший 1/ 2 Uопор. .

Двуполярные : первый разряд дает знак , следующий 0,5 Uопор. ,

n-1

младший 1/2 Uопор. .

-0,51 ё -0,38 ® 000  Декодирование аналогового

-0,38 ё -0,26 ® 001 напряжения в бинарное число

-0,26 ё -0,13 ® 010 DU = 0,128 - шаг квантования.

-0,13 ё 0 ® 011 Uразмаха = 1,024 В.

0 ё 0,13 ® 100 ( ошибка не больше 0,5 DU ).

0,13 ё 0,26 ® 101

0,26 ё 0,38 ® 110

0,38 ё 0,51 ® 111

ОСНОВНЫЕ ТИПЫ ЦАП.

1.Цепочка взвешенных резисторов.

R R Rвх.оу№0 ,Rключей№0 (удается реали-

зовать ключи с сопротивлением R»10 Ом)

2R Uвых~еIвх

4R Недостатки:

ОУ Слишком большой разброс сопротивлений

8R Uвых и как следствие трудность в изготовление

их на одной микросхеме .

Влияние Rвх.оу на цепь.

Uопорное

2.Цепочка R-2R .

+Uопорн

2R Uвых Достоинства:

Более технологична ,т.к.всего два

номинала сопротивлений.

-Uопорн 2R R Rн

2R R

2R R

2R

АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ.

А).АЦП последовательного приближения (скоростные).

xi(t) УВХ Ком- схема Umax

пар. управл Uвх

1/2Umax

ЦАП RG

Uвых Umin

цап  n

вых 1 2 3 4 5

1.При подачи пускового импульса , после УВХ обнуляется регистр (RG),

затем в старший разряд регистра дается “1”,на выходе ЦАП появляется

напряжение равное 0.5Umax .Если Uвых.увх>Uвых.цап ,то ”1” в старшем

разряде остается ( иначе она стирается ).

2.Опять ставят “1” в следующий разряд регистра .......................................

.......................................................................................................................

Кол-во шагов соответствует кол-ву разрядов АЦП.

Б).АЦП параллельного действия .

Uопорн. В качестве опорного на каждый

компаратор (К) подается сетка

УВХ R  напряжений - Uопорн.

xi(t) K n

2 n

R Kол-во компараторов = 2 .

K При подачи сигнала на вход АЦП ,

R ДЕКО- все компараторы у которых

K ДЕР Q2 Uопорн.<Uвх.

дадут единици.

R Q1 Наивысший номер компаратора

K находящегося в единичном состоя-

R Q0 нии соответствует выходному коду

K АЦП.

R Недостатки:

K Эти АЦП малоразрядные (4-5)

R (т.к.необходимо много компара-

K  торов).

R

K

R

КОМПЛЕКСНОЕ ПРЕДСТАВЛЕНИЕ СИГНАЛОВ.

x t)= x(t)+jh(t)=E(t)exp{ jy(t)} x(t) x

`  `

h(t)

пре-

образ.

При определенных правилах связи комплексное число дает аналитический сигнал

( т.е. непрерывный вместе со своими производными ) .

h(t)

E(t) Описание сигнала через огибающюю E(t)

и фазу y(t) .

y(t)

Похожие работы

Дискретизация сигнала

Скачать

16809

0

4

... сигнала уровень квантования называют также глубиной дискретизации или битностью. Глубина дискретизации измеряется в битах и обозначает количество бит, выражающих амплитуду сигнала. Чем больше глубина дискретизации, тем точнее цифровой сигнал соответствует аналоговому. В случае однородного квантования глубину дискретизации называют также динамическим диапазоном и измеряют в децибелах (1 бит ≈ ...

Квантование сообщений. Ошибки квантования. Энтропия источника сообщений

Скачать

14053

0

1

... иметь дело с данными, имеющими конечный размер, – например, с массивами чисел конечного размера и ограниченной разрядности. Рассмотренная выше теорема дискретизации дает такую возможность.   Количество информации, энтропия источника сообщений Для сравнения между собой различных источников сообщений необходимо ввести некоторую количественную меру, которая дала бы возможность объективно ...

Описание сигналов

Скачать

23730

0

8

... функций в виде зависимости их значений от определенных аргументов Δвремени, линейной или пространственной координаты и т.п.) при анализе и обработке данных широко используется математическое описание сигналов по аргументам, обратным аргументам динамического представления. Так, например, для времени обратным аргументом является частота. Возможность такого описания определяется тем, что любой ...

Автоматизированные системы обработки информации и управления

Скачать

326231

12

0

... рисунков в формате А0-А1 со скоростью 10-30 мм/с. Фотонаборный аппарат Фотонаборный аппарат можно увидеть только в солидной полиграфической фирме. Он отличается своим высоким разрешением. Для обработки информации фотонаборный аппарат оборудуется процессором растрового изображения RIP, который функционирует как интерпретатор PostScript в растровое изображение. В отличие от лазерного принтера в ...