Навигация
Параметры транзисторного ключа
4.2. Параметры транзисторного ключа
1. Остаточное напряжение и остаточный ток.
Под остаточным напряжением надо понимать уровень напряжения на выходе открытого до насыщения транзистора. Величина остаточного напряжения находится в прямой зависимости от степени насыщения транзистора: чем глубже насыщение транзистора, тем меньше остаточное напряжение на его выходе. Глубокое насыщение наступает в том случае, если транзистор переходит в режим двойной инжекции: инжекция в базу идет и из эмиттера, и из коллектора. Обычное значение остаточного напряжения на выходе насыщенного биполярного транзистора лежит в пределах Uост=0,05-0,1В. У полевого транзистора эта величина может быть гораздо меньше.
Под остаточным током подразумевается ток неосновных носителей через закрытый транзистор. Его величина очень незначительна и чаще всего им пренебрегают, но при повышении температуры и частоты с ним приходится считаться.
2. Степень насыщения транзистора в схеме ключа. Существует понятие формального критерия насыщения - когда на коллекторе действует прямое напряжение. Но транзистор обычно работает в режиме заданного тока, поэтому для оценки степени насыщения транзистора более удобен токовый критерий
(4.1)
где Iкн - ток насыщения транзистора; b - статический коэффициент передачи тока базы; I+б - отпирающий базовый ток. Чтобы оценить силу неравенства (4.1), вводится особый параметр - степень насыщения S:
(4.2)
3. Быстродействие - время отклика схемы на сигнал, то есть это время, в течение которого транзистор переходит из закрытого состояния в открытое и наоборот. При этом самым важным параметром можно считать среднее время задержки распространения сигнала tср.зд.. Чем глубже насыщение транзистора, тем хуже быстродействие ключа в целом. Чтобы не допустить ощутимой инжекции со стороны коллектора в то время, когда потенциал коллектора изменился на противоположный, коллекторный переход шунтируется диодом Шоттке, падение напряжения на котором не превышает 0,2-0,4 В (рис. 1.8). При этом несколько увеличивается остаточное напряжение на транзисторе, но это окупается высоким быстродействием ключа.
4. Помехоустойчивость - устойчивость схемы против ложного срабатывания.
Статическая помехоустойчивость - максимально допустимое напряжение статической помехи, при которой еще не происходит изменения выходного напряжения. Под статической помехой понимают паразитные напряжения и токи, длительность которых значительно больше времени переключения схемы из одного состояния в другое. Измеряют помехоустойчивость обычно в вольтах. По отношению к полярности входного сигнала помехоустойчивость может быть существенно разной.
Динамическая помехоустойчивость возникает в переходных процессах.
5. Нагрузочная способность ключа.
Типичным для ключевых схем является сочетание нескольких ключей, соединенных последовательно или параллельно. В последовательной цепочке (рис. 4.2) каждый ключ может управлять не одним, а несколькими ключами. Поэтому нагрузочной способностью ключа называют количество параллельно включенных ключей, которыми способен управлять данный ключ.
Рис. 4.2. Ключевая цепочка
В схеме рис. 4.2 показано, что второй транзистор VT2 управляет не только ключом VT3, но и еще рядом ключей - VT4, VT5, VT6.
Величина тока, отпирающего ключ VT2,
(4.3)
где U* - напряжение отпирания эмиттерного перехода втранзисторе; Rк - резистор нагрузки в коллекторной цепи VT1, который играет роль резистора смещения в цепи базы VT2.
Коллекторный ток в последовательной цепочке
Следовательно, коллекторный и базовый токи в последовательной цепочке почти одинаковы.
Обозначим число ключей, нагруженных на VT2, через n. Если допустить, что отпирающий ток (Iб) равномерно распределяется между базами всех параллельных ключей, то в цепи базы каждого ключа будет протекать ток
(4.4)
Отпирающий ток должен удовлетворять токовому критерию насыщения (4.1), из которого можно получить принципиальное ограничение на нагрузочную способность ключа. Кроме того, учитывая, что ограничение должно быть достаточно жестким, то есть необходимо не просто обеспечить насыщение, а
минимальную степень насыщения транзистора Sмин (4.2) получаем
(4.5)
где b - коэффициент передачи базового тока при нормальном включении транзистора.
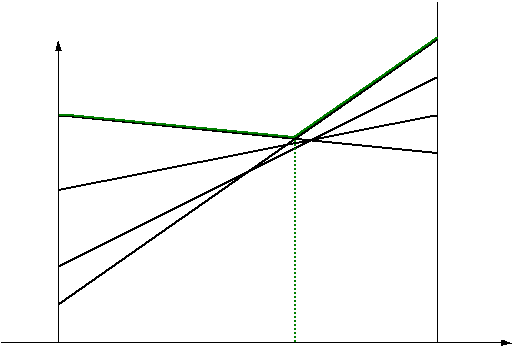
В реальных схемах наблюдается неравномерное распределение токов между базами параллельно соединенных ключей. Дело в том, что крутизна входных ВАХ транзисторов очень высокая и малейшее несовпадение характеристики одного транзистора с характеристикой другого вызывает большой разброс в базовых токах (рис. 4.3)
Чтобы выровнять базовые токи транзисторов необходимо уменьшить крутизну ВАХ. С этой целью последовательно с базами каждого транзистора включают резисторы одного номинала. На рис. 4.2 эти резисторы показаны штриховыми линиями.
|
На рис. 4.3 второй пучок входных ВАХ транзистора соответствует схемам ключей с резисторами в цепях базы. Наклон характеристик соответствует сопротивлению R.
К сведению, сопротивление базы играет ту же роль, что и резистор R, но его величина не превышает 100-150 Ом. За счет сопротивления резистора R общее сопротивление базы будет больше, за счет чего и прямое напряжение на эмиттерном переходе Uэ увеличивается до 1,2 В.
Похожие работы
кую и дидактическую функции с учетом ситуации в российской социологии. Направления фундаментального уровня различаются и систематизируются в концепции преподавания социологической теории на основе их существенной связи с различными решениями важнейших философских, теоретико-познавательных и мировоззренческих проблем, сформулированных в истории европейской социальной мысли относительно природы ...
... смешанными стратегиями игроков 1 и 2 называются такие наборы хо, уо соответственно, которые удовлетворяют равенству Е (А, х, y) = Е (А, х, y) = Е (А, хо, уо). Величина Е (А, хо ,уо) называется при этом ценой игры и обозначается через u. Имеется и другое определение оптимальных смешанных стратегий: хо, уо называются оптимальными смешанными стратегиями соответственно игроков 1 и 2, если они ...
... Доказать: По определению второй смешанной производной. Найдем по двумерной плотности одномерные плотности случайных величин X и Y. Т.к. полученное равенство верно для всех х, то подинтегральные выражение аналогично В математической теории вероятности вводится как базовая формула (1) ибо предлагается, что плотность вероятности как аналитическая функция может не существовать. Но т.к. в нашем ...
... была построена теория вложения функциональных пространств, которые в настоящее время носят название пространств Соболева. А.Н. Тихоновым была построена теория некорректных задач. Выдающийся вклад в современную теорию дифференциальных уравнений внесли российские математики Н.Н. Боголюбов, А.Н. Колмогоров, И.Г. Петровский, Л.С. Понтрягин, С.Л. Соболев, А.Н. Тихонов и другие. Влияние на развитие ...
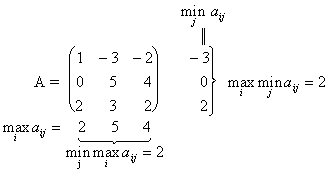
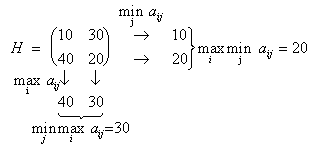





0 комментариев