Навигация
Частотные и импульсные свойства p-n-перехода
1.2.2. Частотные и импульсные свойства p-n-перехода
При воздействии на p-n-переход напряжения высокой частоты начинают проявляться инерционные свойства перехода: распределение носителей при достаточно быстрых изменениях тока или напряжения требует определенного времени. Внешнее напряжение изменяет ширину запрещенной зоны, высоту потенциального барьера, граничную концентрацию носителей (величину объемных зарядов в переходе), следовательно, p-n-переход обладает емкостью. Для p-n-перехода характерны два состояния (прямо- и обратносмещенное), поэтому эту емкость можно условно разделить на две составляющие - барьерную и диффузионную. Деление емкостей на барьерную и диффузионную является чисто условным, но, учитывая тот факт, что значения их сильно отличаются, на практике понятие барьерной емкости удобнее использовать для обратносмещенного p-n-перехода, а диффузионной - для прямосмещенного.
Барьерная емкость отражает перераспределение носителей в p-n-переходе, то есть эта емкость обусловлена нескомпенсированным объемным зарядом, сосредоточенным по обе стороны от границы перехода. Роль диэлектрика у барьерной емкости выполняет запрещенная зона, практически лишенная носителей. Барьерная емкость зависит от площади перехода, от концентрации примеси, от напряжения на переходе:
где П - площадь p-n-перехода (в зависимости от площади перехода барьерная емкость может изменяться от единиц до сотен пикофарад); x - диэлектрическая проницаемость полупроводникового материала; Nд - концентрация примеси; U - напряжение на переходе.
Значение барьерной емкости колеблется от десятков до сотен пФ. При постоянном напряжении на переходе барьерная емкость определяется отношением , а при переменном .
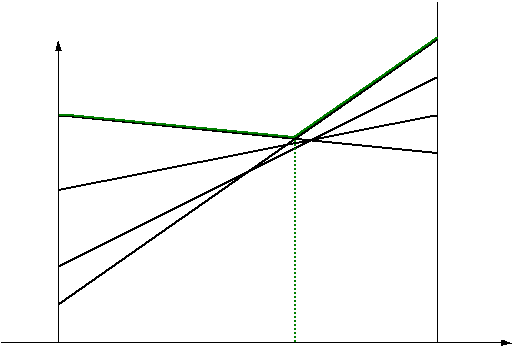
Особенностью барьерной емкости является то, что она изменяется при изменении напряжения на переходе (рис. 1.2); изменение барьерной емкости при изменении напряжения может достигать десятикратной величины, то есть эта емкость нелинейна, и при увеличении обратного напряжения барьерная емкость уменьшается, так как возрастает толщина запирающего слоя (площадь p-n-перехода).
Рис. 1.2. Зависимость барьерной емкости от напряжения
В силовых полупроводниковых приборах площадь p-n-перехода делается большой, поэтому у них велика величина барьерной емкости. Такие полупроводниковые диоды называют плоскостными. Если такой прибор использовать, например, для выпрямления переменного напряжения высокой частоты в постоянное, то барьерная емкость, зашунтировав переход, нарушает его одностороннюю проводимость, то есть переход теряет выпрямительные свойства, поэтому частотный диапазон плоскостных диодов ограничивается промышленными частотами. Но барьерная емкость может быть и полезной: приборы с явно выраженными емкостными свойствами (варикапы) используются для электронной перестройки контуров.
У точечных p-n-переходов площадь перехода мала, поэтому барьерная емкость невелика и частотный диапазон гораздо шире, чем у плоскостных.
Диффузионная емкость отражает перераспределение носителей в базе:
где t - время жизни носителей; Iпр - прямой ток через диод.
Значение диффузионной емкости колеблется от сотен до тысяч пФ.
Диффузионная емкость также нелинейна и возрастает с увеличением прямого напряжения. Образование этой емкости схематично можно представить следующим образом. Эмиттером будем считать p-область, а базой n-область. Носители из эмиттера инжектируются в базу. В базе вблизи перехода происходит скопление дырок - объемный положительный заряд, но в это время от источника прямого напряжения в n-область поступают электроны, и в этой облаcти, ближе к внешнему выводу, скапливается отрицательный объемный заряд. Таким образом, в n-области наблюдается образование двух разноименных зарядов "+Qдиф" и "-Qдиф". При постоянном напряжении эта емкость рассматривается как отношение абсолютных значений заряда и контактной разности потенциалов (прямого напряжения):
,
а при переменном
.
Так как вольт-амперная характеристика перехода нелинейна, то с увеличением внешнего напряжения прямой ток растет быстрее, чем прямое напряжение на переходе, поэтому и заряд "Qдиф" растет быстрее, чем прямое напряжение, и диффузионная емкость тоже увеличивается.
Диффузионная емкость является причиной инерционности полупроводниковых приборов при работе в диапазоне высоких частот и в режиме ключа, так как процесс накопления и особенно рассасывания объемного заряда требует затраты определенного времени.
На рис. 1.3, а, б и рис. 1.4, а, б даны упрощенные эквивалентные схемы полупроводникового перехода (простейшего диода) на низких и высоких частотах.
На низких частотах сопротивления диффузионной и барьерной емкостей очень велики и не оказывают шунтирующего действия на переход, поэтому они не подлежат учету.
|
Рис. 1.3. Эквивалентные схемы перехода на низких частотах: а - для диффузионной емкости (Сдиф); б - для барьерной емкости (Сбар).
Сопротивление емкости в общем случае
(1.7)
где rp-n- сопротивление прямосмещенного p-n-перехода; rобр - сопротивление обратносмещенного p-n-перехода (rобл< rпр<< rобр); rобл - суммарное сопротивление n- и p-областей и контактов этих областей с выводами.
|
Рис. 1.4. Эквивалентные схемы перехода на высоких частотах: а - для диффузионной емкости (Сдиф); б - для барьерной емкости (Сбар).
Диффузионная емкость значительно больше барьерной, но использовать ее для практических целей нельзя, так как она зашунтирована малым сопротивлением прямосмещенного p-n-перехода.
Импульсные диоды используют в качестве ключевых элементов в устройствах с микросекундной и наносекундной длительностью импульсов
(рис. 1.5).
Важным параметром при этом будет время восстановления обратного сопротивления tвос - интервал времени от момента переключения до момента, когда обратный ток уменьшается до заданного уровня отсчета; при подаче на диод запирающего импульса ток не может мгновенно уменьшиться до нуля, так как в базе образовался объемный заряд и на его рассасывание требуется определенное время. Этим и объясняется выброс обратного тока в цепи диода (рис. 1.5, б).
|
Рис. 1.5. Диод в импульсном режиме: а - схема простейшего ключа;
б - временные диаграммы входного напряжения и тока через диод
Похожие работы
кую и дидактическую функции с учетом ситуации в российской социологии. Направления фундаментального уровня различаются и систематизируются в концепции преподавания социологической теории на основе их существенной связи с различными решениями важнейших философских, теоретико-познавательных и мировоззренческих проблем, сформулированных в истории европейской социальной мысли относительно природы ...
... смешанными стратегиями игроков 1 и 2 называются такие наборы хо, уо соответственно, которые удовлетворяют равенству Е (А, х, y) = Е (А, х, y) = Е (А, хо, уо). Величина Е (А, хо ,уо) называется при этом ценой игры и обозначается через u. Имеется и другое определение оптимальных смешанных стратегий: хо, уо называются оптимальными смешанными стратегиями соответственно игроков 1 и 2, если они ...
... Доказать: По определению второй смешанной производной. Найдем по двумерной плотности одномерные плотности случайных величин X и Y. Т.к. полученное равенство верно для всех х, то подинтегральные выражение аналогично В математической теории вероятности вводится как базовая формула (1) ибо предлагается, что плотность вероятности как аналитическая функция может не существовать. Но т.к. в нашем ...
... была построена теория вложения функциональных пространств, которые в настоящее время носят название пространств Соболева. А.Н. Тихоновым была построена теория некорректных задач. Выдающийся вклад в современную теорию дифференциальных уравнений внесли российские математики Н.Н. Боголюбов, А.Н. Колмогоров, И.Г. Петровский, Л.С. Понтрягин, С.Л. Соболев, А.Н. Тихонов и другие. Влияние на развитие ...
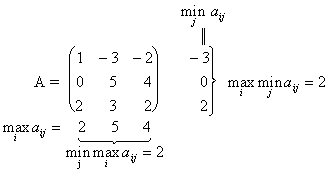
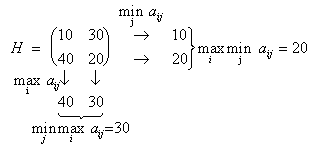





0 комментариев