Навигация
Выявление основной тенденции ряда. Аналитическое выравнивание
2.3. Выявление основной тенденции ряда. Аналитическое выравнивание.
Наиболее эффективным способом выявления основной тенденции развития является аналитическое выравнивание. При этом уровни ряда динамики выражаются в виде функции времени.
Аналитическое выравнивание является предпосылкой для применения других приемов углубленного изучения развития социально - экономических явлений во времени, для изучения колеблемости данных в динамике, их связи с другими явлениями.
В практике социально-экономических исследований применяется аналитическое выравнивание по прямой, параболе второго и третьего порядка, гиперболе, экспоненте. Аналитическое выравнивание состоит в подборе для данного ряда динамики теоретической кривой, выражающей основные черты фактической динамики, т.е. в подборе теоретически плавной кривой, наилучшим образом описывающей эмпирические данные.
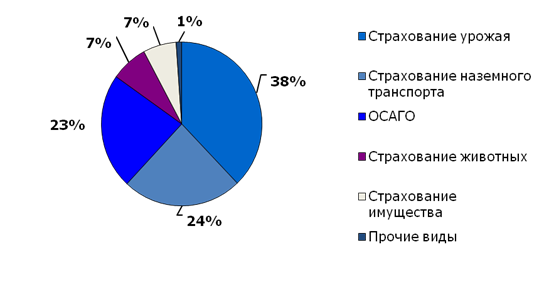
Проанализируем данные по страховым выплатам по видам страховой деятельности, используя таблицу 7.
Таблица7.
| период времени | личное страхование, млн. руб., y | t | tІ | yt | yt |
| 1992 | 11.16 | -7 | 49 | -78,12 | -4164,90 |
| 1993 | 259.74 | -5 | 25 | -1298,7 | 72,26 |
| 1994 | 2877.83 | -3 | 9 | -8633,49 | 4309.42 |
| 1995 | 9159.33 | -1 | 1 | -9159,33 | 8546,58 |
| 1996 | 10229.11 | +1 | 1 | 10229,11 | 12783,74 |
| 1997 | 10679.17 | +3 | 9 | 32037,51 | 17020,90 |
| 1998 | 15955.41 | +5 | 25 | 79777,05 | 21258,06 |
| 1999 | 36149.54 | +7 | 49 | 253046,78 | 25495,22 |
| ИТОГО | 85321,29 | 168 | 355920,81 | 85321,29 |
Произведем аналитическое выравнивание по прямой. Для этого используем выражение:
y0= a0 + a1t , где t - условное обозначение времени, а а0 и а1 - параметры искомой прямой.
Параметры прямой, удовлетворяющей методу наименьших квадратов, находятся из решения системы уравнений:
na0 + a1t = y
a0t + atІ = yt , где y - фактические уровни, n - число членов ряда динамики.
Система упрощается, если t подобрать так, чтобы их сумма равнялась нулю, т.е. начало отсчета времени перенести в середину рассматриваемого периода. Тогда
а0 = y/n ; a1 = yt/tІ
Поскольку число уровней четное (n = 8), то распределение при t = 0 будет следующим (3-я колонка в таблице 7).
Из таблицы находим:
n = 8; y = 85321,29; yt = 355920,81; tІ = 168.
a0 = 85321,29/8 = 10665,16; a1 = 355920,81/168 = 2118,58
Уравнение прямой будет иметь вид: yt= 10665 + 2118,58t
По уравнению найдем расчетные значения выровненных уровней ряда динамики (последняя колонка в таблице 7).
Графически результаты произведенного аналитического выравнивания ряда динамики страховой деятельности и фактические данные будут выглядеть следующим образом:
Рис.1.
Сумма уровней эмпирического ряда (y) совпадает с суммой расчетных значений выравненного ряда yt. А полученное уравнение показывает, что сумма личного страхования растет приблизительно на 4200 млн.руб. в год.
Мы произвели аналитическое выравнивание ряда динамики личного страхования по прямой. Рассмотрим данные по обязательному страхованию и произведем выравнивание по многочлену более высокой степени - по параболе второго порядка:
yt = a0t + a1t + a2tІ Для произведения расчетов вновь воспользуемся данными, взятыми из таблицы 4.
Таблица 8.
| период времени | обязательное страхование, млн. руб., y | t | tІ | t | yt | ytІ | yt |
| 1992 | 1.10 | -7 | 49 | 2401 | -7,70 | 53,90 | -348,55 |
| 1993 | 61.83 | -5 | 25 | 625 | -309,15 | 1545,75 | 47,97 |
| 1994 | 1225.57 | -3 | 9 | 81 | -3676,71 | 11030,13 | 1268,25 |
| 1995 | 6020.25 | -1 | 1 | 1 | -6020,25 | 6020,25 | 3312,29 |
| 1996 | 10974.17 | +1 | 1 | 1 | 10,974,17 | 10974,17 | 6180,09 |
| 1997 | 12747.47 | +3 | 9 | 81 | 38242,41 | 114727,23 | 9871,65 |
| 1998 | 13606.40 | +5 | 25 | 625 | 68032,0 | 340160,0 | 14385,22 |
| 1999 | 19094.38 | +7 | 49 | 2401 | 133660,66 | 935624,62 | 19725,75 |
| ИТОГО | 63731,17 | 168 | 6216 | 240895,43 | 1420135,80 | 59442,67 |
Система нормальных уравнений для определения параметров параболы принимает вид:
na0 + a1t + a2tІ = y
a0t + a1tІ + a2tі = yt
a0tІ + a1tі + a2t = ytІ
Как видно из таблицы t = 0, также tі = 0, следовательно, система упрощается:
na0 + a2tІ = y
a1tІ = yt
a0 + a2yt = ytІ
Отсюда получается, что a1 = yt/tІ = 1433,90 ;
a0и a2 определяются из решения системы двух уравнений с двумя неизвестными:
10a0 + 168а2 = 63731,17
168а0 + 6216а2 = 1420135,80 ,или
а0 + 16,8а2 = 6373,117
а0 + 37а2 = 8453,19
Отсюда 20,2а2 = 2080,07
а2 = 102,97
а0 = 4643,22
Уравнение параболы: yt = 4643,22 + 1433,90t + 102,97tІ
Расчетные данные для каждого года приводятся в последней колонке таблицы 8. Мы видим некоторые расхождения между суммой выровненных и фактических данных. Это происходит из-за округления величин, а также наличия более высоких степеней в системе уравнения для определения параметров параболы, чем, например, прямой. Для более наглядного рассмотрения рассчитанных показателей, воспроизведем графически результаты, полученные аналитически.
Рис. 2
Как мы видим, выровненные данные действительно представляют собой параболу.
Параметры уравнения параболы интерпретируются следующим образом: а0 - величина, выражающая средние условия образования уровней ряда, а1 - скорость развития данных ряда динамики, а2 - ускорение этого раз
Похожие работы
... (2.31.) Страховой тариф лежит в основе определения эффективности страховых операций как системы показателей, характеризующей экономическую целесообразность проведения различных видов страхования. 2.4. Статистический анализ и показатели эффективности страхования Основным показателем эффективности страхования является рентабельность в виде обычного отношения годовой балансовой прибыли к ...
... , характеризующие отдельные стороны деятельности страховых организаций. В следующем подразделе более подробно рассмотрим основные показатели финансово-хозяйственной деятельности страховых организаций.[22] 1.3 Методология анализа показателей финансово-хозяйственной деятельности страховых организаций Основными финансовыми показателями деятельности страховой организации служат: ...
... – 199 с. 18. http://www.ingos.ru/ru/about/finance/2006 Журналы: Страховое дело, Страховое ревю, Финансы, Финансовый бизнес, Страховое право. Газеты: Финансовая газета, Экономика и жизнь, Страховая газета. Приложение Бухгалтерский баланс ОСАО "Ингосстрах" на 31.12.2006 (тыс.руб) АКТИВ Код строки На начало отчетного года На конец отчетного периода I. Активы ...
... стран- участниц ЕС: введение единых правил по финансовым гарантиям страховщиков, единых правил лицензирования, определение ответственности национальных органов надзора за страховой деятельностью, введение единой классификации видов страхования. Итак, различия государственного регулирования страховой деятельности в Российской Федерации и за рубежом (на примере Европейского союза) очевидны
0 комментариев