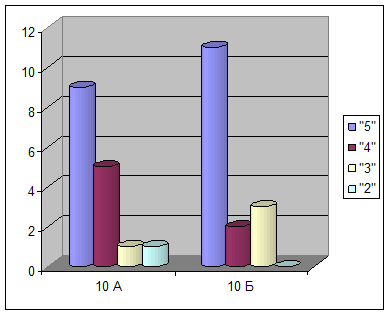
Наглядно, обозримо, выразительно

1.    наглядно, обозримо, выразительно.

2.    сразу видны пределы изменения показателя, сравнительная скорость изменения и колеблемость

Минусы графического изображения

Включают меньшее количество данных чем в таблице. на графике показываются округленные данные, общая ситуация, но не детали.
Тема 3: Статистические показатели.

§1. Сущность и значение статистического показателя, его атрибуты.

§2. Классификация статистических показателей.

§3. Виды относительных показателей. Принципы построения.

§4. Системы статистических показателей.

§1.

Статистический признак – свойство присущее ЕСС, он существует объективно от того изучает его как наука или нет

Статистический показатель – обобщающая характеристика какого-либо свойства совокупности.

Структура статистического показателя (его атрибуты):

Качественная сторона : объект и его свойства	Количественная сторона: число и ед. измерения	Территориальные, отраслевые, либо др. границы	Интервал или момент времени
Ввод в действие жилых домов	40800,5 млн./м2	РФ	1993 год

§2.

·     Средние величины

·     Показатели вариации

·     Показатели связи признаков

·     Показатели структуры и характера распределения

·     Показатели динамики

·     Показатели колебимости

·     Показатели точности и надежности выборочных оценок

·     Показатели точности и надежности прогнозов

По виду: суммарное количество единиц либо суммарное свойство объекта. Это сумма первичных признаков, измеряется в шт., кг, м, $, и т.д.

Относительный показатель – получаемый путем сопоставления абсолютных или относительных показателей в пространстве, во времени или в сравнении показателей разных свойств изучаемого объекта.

Относительный показатель 1^го порядка получается путем сопоставления 2^х абсолютных показателей. Относительный показатель 2^го порядка получается путем сопоставления относительных показателей 1^го порядка и т.д.

Относительный показатель 3^го порядка и выше встречаются очень редко.

Прямые показатели – такие показатели величина которых увеличивается с увеличением исследуемого явления .

Обратные показатели – показатели величина которых уменьшается с увеличением исследуемого явления.

Пример:

§3. Относительные показатели

Показатели структуры получаются путем отношения части к целому.

Относительные показатели динамики

ü  Показатели динамики (темпы роста, прироста)

ü  Индексы

Показатели взаимосвязи характеризуют связи между признаками:

ü  Коэффициент корреляции

ü  Аналитические индексы

Показатели интенсивности характеризуют отношение двух объектов по разным признакам.

ü  Трудоемкость – количество времени используемое для изготовления одной единицы изделия

ü  Выработка – количество продукции произведенное в единицу времени

ВЫРАБОТКА = 1/трудоемкость

Показатели отношения к нормативу – соотношение фактических величин признака показателя к нормативным, плановым, оптимальным.

Показатели сравнения – сравнение разных объектов по одному признаку.

Общие принципы построения статистических показателей:

1.    статистические показатели объективно связаны.

2.    сравниваемые показатели могут отличаться только одни атрибутом, нельзя сопоставлять показатель по двум и более атрибутам.

3.    необходимо знать и учитывать границы показателя.

§4.

Для каждой характеристики объекта необходима система статистических показателей.

1.    функция позновательская – основывается на анализе данных

2.    пропагандистская

3.    стимулирующая функция

тема 4: Средние величины

§1. понятие средней величины

§2. виды средних величин

§3. средняя арифметическая и ее свойства

§4. среднее гармоническое, геометрическое, квадратическое.

§5. многомерная средняя

§1.

Наиболее распространенной формой статистических показателей является средняя величина.

Важнейшее свойство средней заключается в том, что она отражает то общее, что присуще каждой единице изучаемой совокупности, хотя значение признака отдельных единиц совокупности могут колебаться в ту или иную сторону.

Типичность средней непосредственно связана с однородностью изучаемой совокупности. В случае не однородной совокупности необходимо провести разбивку ее на качественно однородные группы и рассчитать среднюю по каждой по каждой из однородных групп.

Определить среднюю можно через исходное соотношение средней (ИСС) ее логическую формулу.

От того в каком виде представлены данные для расчета средней, зависит каким именно будет ИСС.

§2.

Средняя арифметическая Средне гармоническая Средне квадратическая, кубическая Средне геометрическое

Правило мажерантности средних.

Структурные средние

Мода – Мо

Медиана – Ме

В рядах динамики рассчитывается средняя арифметическая, средняя хронологическая.

Средней арифметической называется такое среднее значение признака при вычислении которого общий объем признака не изменяется.

Пример: вес.

 - ср. арифметическое простое

x_i – индивидуальное значение признака

n – общее число изучаемой совокупности

 ср. арифметическое взвешенное

Свойства ср. арифметической.

Сумма отклонений индивидуальных значений признака от его средней величины равно нулю если каждое индивидуальное значение признака умножить или разделить на одно и тоже постоянное число, то среднее увеличится или уменьшится во столько же раз. если к каждому индивидуальному значению признака прибавить одно и тоже постоянное число, то средняя величина изменится соответственно на тоже самое число.

Доказательство

если веса f средней взвешенной умножить или разделить на одно и тоже число, то средняя не изменится. сумма квадратов отклонений признака меньше чем от любого другого числа.

Другие виды средних

Вид средней	Простая средняя	Взвешенная средняя
гармоническая
геометрическое
Квадратическая

§5.

Очень трудно охарактеризовать группировку по одному признаку и мало остается информации в памяти.

Сохранить сложность описания групп и одновременно преодолеть недостатки комбинированной группировки позволяют многомерные группировки. Простейшим вариантом многомерной группировки является многомерная средняя.

Многомерная средняя – средняя величина для нескольких признаков Е.С.С.

Т.к. нельзя рассчитать ср. величину абсолютных значений разных признаков выраженных в разных единицах измерения, то многомерная средняя вычисляется из относительных величин.

Из отношений значений признака для Е.С. к средним значениям этих признаков.

 - многомерная средняя для i единицы

x_ij – значение признака j для i единицы

 - среднее значение признака j

k – число признаков

j – номер признака и номер его совокупности

тема 5: Вариационный анализ

§1. Вариация признаков и ее причины

§2. Ряды распределения

§3. Структурные характеристики вариационного ряда.

§4. Показатели силы вариации.

§5. Показатели интенсивности вариации

§6. виды дисперсии. Правило сложения дисперсии.

§1.

Вариацией значения какого-либо признака в совокупности называется различие его значений у разных единиц данной совокупности в один и тот же период или момент времени.

Причина вариации: разные условия существования ЕСС именно вариация порождает необходимость в такой науке как статистика.

§2.

Проведение вариационного анализа начинается с построения вариационного ряда – упорядоченное распределение единиц совокупности по возрастающим или по убывающим признакам и подсчет соответствующих частот.

Ряды распределения

ü  ранжированные

ü  дискретные

ü  интервальные

Ранжированный вариационный ряд – перечень отдельных ед. совокупности в порядке возрастания убывания ранжированного признака

БАНК	Капитал тыс. руб.
СБ РФ	96007237
Внешторгбанк	47991724

Дискретный вариационный ряд – таблица состоящая из 2^х строк – полимерных значений варьирующего признака и кол-во единиц с данным значением признака.

Кол-во детей в семье	0	1	2	3	4
Кол-во семей	20	40	45	10	5

Интервальный вариационный ряд строится в случаях:

1.    признак принимает дискретные значения , но кол-во их слишком велико

2.    признака принимает любые значения в определенном диапазоне

Размер собственного капитала тыс. руб.	0 - 10000	10000-50000	Свыше 50000
Количество банков	20	40	10

При построении интервального вариационного ряда необходимо выбрать оптимальное количество групп, самый распространенный способ по формуле Стерджесса

k=1+3.32lgn

k – количество интервалов

n – объем совокупности

При расчетах почти всегда получают дробные значения, округления производить до целого числа.

Длина интервала – l

Виды интервалов

1.    нижняя граница последующего интервала повторяет верхнюю границу последующего интервала

0 - 10	10 - 20	20 - 30

2.    С индивидуальными границами в интервал входят верхняя и нижняя границы

0 - 9	10 - 19	20 - 29

3.    открытый интервал, интервал с одной границей

До 5	5 - 10	10 – 15

В случае открытого интервала l принимается равной длине смежного с ним интервала, либо исходя из логических соображений.

Стаж	До 5	5-7	7-9
Кол-во рабочих

При расчетах по интервальному вариационному ряду за x_i принимается середина интервала.

Интервалы могут быть как равные так и нет. При изучении вариационного ряда существенную помощь оказывает графическое изображение. Дискретный вариационный ряд изображается с помощью полигона.

Интервальный вариационный ряд изображается с помощью гистограммы.

Накопленная частота

xi	0	1	2	3	4
fi	20	40	45	10	5

N_ME=60 медиана = 1

Кумулята – распределение меньше чем

Огива – распределение больше чем

§3.

Медиана – значение признака делящее всю совокупность на две равные части.

Для дискретного вариационного ряда расчет медианы: если n-четное, то №_Ме медианой единицы

Интервальный вариационный ряд:

k – количество интервалов

х₀ – нижняя граница медианного интервала

l – длина медианного интервала

 - сумма частот

 - накопленная частота интервала предшествующая медианному.

 - частота медианного интервала

Медианный интервал – первый интервал накопленная частота которого превышает половину от общей суммы частот.

0-5	5-10	10-15	15-20
15	20	40	25

Графически медиана находится по кумуляте.