Понятие группировки,
группировочные
признаки, интервалы
групп, их виды,
порядок определения
Статистические
таблицы, основные
правила их
составления
и оформления
Средние
величины, их
виды, формулы
Понятие
рядов динамики,
их виды, особенности
Общие, групповые
индексы, порядок
их построения
Корреляционный
метод анализа
между явлениями
Навигация
Корреляционный метод анализа между явлениями
Шпаргалки
46647
знаков
1
таблица
0
изображений
27 Корреляционный метод анализа между явлениями.
33 Парная корреляция и линейная регрессия.(часть, см. 32)
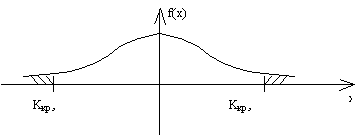
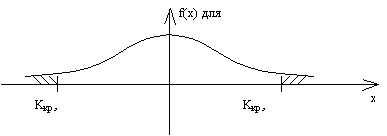
При проведении корреляционного анализа необходимо отобрать наиболее существенные признаки, установить связь между ними (причинно-следственную) определить форму связи, выбрать математическое уравнение для отражения данных взаимосвязи. При этом необходимо также рассчитать числовые характеристики корреляционной связи, рассмотреть ст. оценку показателей регрессии и тесноты связи. При исследовании взаимосвязи, т.е. при установлении характера взаимосвязи между признаками, кроме аналитической группировки большое значение имеет графический метод. Отложив на оси абсцисс значение факторного признака 'x', а на оси ординат значение результативного признака 'y', и получив в корреляционном пространстве точки 'x' и 'y', получим корреляционное поле. Характер расположения этих точек дает представление о направлении, силе связи, форме связи, а также позволяет построить уравнение парной зависимости.
а) Прямая линия:
б) Парабола:
в) Гипербола:
- результативный признак; x – факторный признак; a0, a1, a2… - параметры уравнения (коэффициенты регрессии), которые позволяют рассмотреть среднее значение, т.е. показывают среднее изменение зависимой переменной y от x при изменении независимой переменной x на 1. Параметры уравнения (свободные члены) определяются путем решения системы нормальных уравнений, полученных на основе метода наименьших квадратов:
а) прямая: ;;
б) парабола
Наряду с построением и решением уравнения связи определяется степень тесноты этой связи при помощи коэффициента линейной регресси r, корреляционного отношения h и индекса корреляции I.
Рассмотрим формулы коэффициента корреляции для несгруппированныхданных: показатель дисперсии
разность между показателями
При изучении тесноты связи с помощью коэффициента корреляции можно проанализировать шкfлу Чеддока, учитывая коэффициент корреляции.
| Величина коэффициента корреляции | Параметры связи |
| До – 0,3 | Связь отсутствует |
| От 0,3 до 0,5 | Связь слабая |
| От 0,5 до 0,7 | Связь умеренная |
| До 1 | Связь сильная |
Для криволинейной зависимости существует корреляционное отношение h, которое является наиболее точным измерителем (показателем) тесноты связи между двумя признаками
; ;
Показатель индекса корреляции рассматривается на основе прямой и обратной взаимосвязи. Все показатели корреляции можно рассматривать с точки зрения случайности данного события и вероятности.
Для определения вероятности достоверности коэффициента корреляции в нормальном распределении применяется критерий t, критерий Стъюдента. Существует специальная таблица критерия Стъюдента, где рассматривается значение вероятности, коэффициент свободы и нормальное распределение. Расчет показателя критерия Стъюдента определяется по следующей формуле:
или или ; где n – число единиц совокупности; r – коэффициент корреляции;
Данный критерий сравнивают с табличным, на основе чего делается вывод о принятии или опровержении выдвинутой гипотезы.
Оценку значимости коэффициента корреляции можно определить по формуле
;
Коэффициент корреляции и значение t в случае превышения расчетного t над табличным и в случае определения параметров регрессии по значимости определяется значение уровня данной значимости и значение степеней свободы n. Значимость определяется коэффициентом a.
29 Понятие выборочного наблюдения. Виды выборок.
Выборочное наблюдение представляет собой один из наиболее широко применяемых видов несплошного наблюдения. При проведении выборочного наблюдения, изучают не все единицы изучаемого объекта, или иными словами, обследуются не все единицы генеральной совокупности, а лишь некоторая отобранная часть единиц. Наблюдение организованно т.о., что эта часть отобранных единиц в уменьшенном масштабе репрезентирует (представляет) всю совокупность. Часть единиц генеральной совокупности, подлежащая непосредственному наблюдению, называется выборочной совокупностью. Система отбора единиц и способов характеристики изучаемой совокупности составляет основу выборочного метода. В расчетах выборочного метода рассматривается следующие показатели
Средняя дисперсия СКО (среднеквадратичное отклонение);
Теория вероятности;
Рассматривая подробно показатели выборочного метода, можно обнаружить ошибки, которые представляют собой ошибки регистрации и ошибки репрезентативности.
По виду отбора различают индивидуальный, групповой и комбинированный отбор. При индивидуальном отборе в выборочной совокупности отбираются отдельные единицы совокупности. При групповом отборе – качественно-однородные группы или серии изучаемых единиц. В комбинированном отборе происходит сочетание первого и второго отбора.
По методу отбора выборка делится на повторную и бесповторуную. При повторной выборке количество единиц остается постоянным, т.е. при выборке рассматриваются все единицы и в генеральную совокупность после регистрации попадают те же самые единицы. По типу возвращающего шара, т.е. при повторном отборе прежде выбранная единица рассматривается и попадает в генеральную совокупность несколько раз.
При бесповторной выборке единиц совокупности попавшая в выборку единица не возвращается в генеральную совокупность, т.е. в дальнейшей выборке она не участвует. И последующую выборку делают из генеральной совокупности уже без отобранных ранее единиц (не возвращающийся шар). Численность единиц в генеральной совокупности при исследовании сокращается. По степени охвата единиц совокупности различают большую и малую выборку.
При малой выборке количество отобранных единиц всегда
Похожие работы
... неравенство |xi|/t>=1. Учитывая это неравенство получаем: P{|X|>=t}=сумма по i: |xi|>=t pi <=сумма по i:|xi|>=t |xi|/t pi<=сумма по i:|xi|>=t |xi|/t pi+сумма по i:|xi|<t |xi|/t*pi =1/t сумма по i от 1 до бесконечности |xi|*pi=1/t*M|X|. 2) Для Н.С.В. Х. Пусть Х – Н.С.В. с плотностью вероятности р(х). Вероятность того, что |X|>=t, равна сумме интегралов от плотности ...
... измерений на рабочем месте. Чтобы эти службы эффективно выполняли стоящие перед ними задачи необходимо научное, техническое и правовое обеспечение их деятельности. Научной основой МО является метрология - наука об измерениях. Техническую основу МО составляют: система государственных эталонов единиц ФВ; система передачи размеров единиц ФВ от эталонов всем средствам измерений с помощью образцовых ...
... их можно периодически менять, делая вид, что сломался карандаш или кончилась ручка. Один юный талант умудрился на ручке иголкой нацарапать ответы на все вопросы теоретического экзамена в ГАИ. Сигареты - шпаргалки помешаются в патроны сигарет, вместо табака. На сигаретах можно проставит номера билетов или краткое название темы вопроса. Пачка сигарет помещается на стол и лежит там в течении всего ...
... ее в рукав пиджака. Причем прикрепляют шпору на резинке. Держат бумажку в ладони и списывают. А как только на горизонте показался преподаватель, просто отпускают ее, и шпаргалка самостоятельно “запрыгивает” обратно. Бывают, конечно, и более изощренные виды шпаргалок. Алексей М., студент факультета социологии СПбГУ, смастерил для сдачи экзаменов волшебную ручку — с увеличительным стеклышком. ...
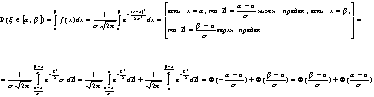
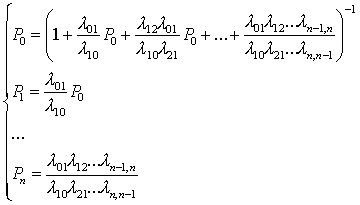
0 комментариев