ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

2. ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

2.1. Методика исследований

Современные исследования тепловых агрегатов напрямую связаны с использованием математических моделей. Это объясняется сложностью и нестабильностью процессов, происходящих в печах. Математическая модель, если она достаточно адекватно описывает поставленную задачу, позволяет исследователю проанализировать влияние различных факторов на те или иные параметры, получить достоверные денные, на основании которых можно сделать выводы и в конечном итоге дать конкретные рекомендации.

Это существенно ускоряет и удешевляет процесс исследования, а в ряде случаев позволяет изучить процессы, ранее недоступные. Для исследования процессов теплообмена в колпаковых печах создана математическая модель, включающая в себя ряд уравнений с граничными условиями, описывающих эти процессы с определенными допущениями. Корректность математической модели определяется обоснованностью принятых при ее разработке допущений и правильностью ее адаптации к реальным условиям. В задачу данной работы и входит выполнение процесса привязки модели к конкретным условиям работы относительно АО «ММК».

2.1.1. Описание исследуемого объекта.

Используемая в дипломной работе математическая модель тепловой работы колпаковой печи была разработана на кафедре ТЭМП Московского государственного института стали и сплавов (Технологического университета) профессором кафедры Мастрюковым Б.С. и доцентом Гусевым Е.В. и опробована в условиях КарМК (Карагандинского металлургического комбината)./ /

Цель данной работы: выявить возможность применения данной модели к условиям работы Магнитогорского металлургического комбината, в частности, ЛПЦ-5.

При разработке математической модели колпаковой печи приняты следующие допущения:

1.   Все температурные поля в печи имеют осевую симметрию.

2.   Температурное поле рулонов принято двухмерным.

3.   Температурное поле футеровки рассчитывается как температурное поле пластины и является одномерным.

4.   Муфель является термически тонким телом.

5.   Излучение и отражение поверхностных зон внешнего контура является изотропным.

6.   Излучение и поглощение внутренней поверхности футеровки колпака и наружной поверхности муфеля не является селективной, то есть e¹f(l).

7.   Защитный газ лучепрозрачен.

8.   Топливовоздушная смесь сгорает мгновенно и пространство между колпаком и муфелем заполнено продуктами сгорания.

9.   Условные замыкающиеся поверхности.

Математическая модель включает в себя уравнения теплового баланса элементов печи, а также уравнения теплообмена и теплопередачи с соответствующими граничными условиями. В данной модели принят зональный метод расчета, при котором все рабочее пространство печи разбивается на зоны. В пределах каждой зоны температура и теплофизические параметры остаются постоянными. Цикл термообработки в колпаковых печах состоит из нагрева, выдержки и охлаждения. Теплообмен печи во всех трех периодах описывается одними и теми же уравнениями, только для периода охлаждения, когда снимают колпак, расчет теплообмена во внешнем контуре заменяется расчетом теплообмена с окружающей средой.

Во внутреннем контуре теплоперенос осуществляется излучением от муфеля к рулонам, а также конвекцией к защитному газу и от защитного газа к рулонам. Таким образом, в математическую модель теплообмена в этом контуре вошли уравнения теплопереноса теплопроводностью в рулоне, уравнения переноса тепла излучением в лучепрозрачной среде, а также уравнения теплового баланса защитного газа.

Математическая модель позволяет определять температурные поля садки, футеровки, муфеля, а также температуры продуктов сгорания и защитного газа в зависимости от изменения различных режимных параметров, как то: расход топлива, его калорийность, массивность садки и прочее. Кроме того, в модель входит блок управления печью с помощью которого можно задавать различные расходы газа на нагреве и выдержке, изменять вид регулирования как в период нагрева, так и в период выдержки.

1.   В начальный момент времени имеются все температурные поля элементов печи: футеровки, муфеля, садки, защитного газа.

2.   Рассчитываем геометрические угловые коэффициенты излучения в наружном и во внутреннем контурах теплообмена.

3.   Производим расчет горения газа.

4.   Рассчитываем теплообмен в наружном контуре:

4.1. По известным температурам продуктов сгорания находим скорость их движения в пространстве между муфелем и колпаком.

4.2. Рассчитываем коэффициенты теплоотдачи конвекцией от продуктов сгорания к муфелю и футеровке, а также от наружной поверхности колпака в окружающую среду.

4.3. Вычисляем радиационные характеристики продуктов сгорания А_пс и e_пс.

4.4. Рассчитываем и нормируем матрицы обобщенных и обобщенных разрешающих коэффициентов излучения.

4.5. По формулам:

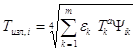, (1)

где m - количество расчетных зон, принимающих участие в теплообмене излучением с зоной «i»;

e_к - степень черноты зоны «к»;

Т_к - температура зоны «к»;

Y_{i, k} - обобщенный разрешающий угловой коэффициент

и

, (2)

где s₀ - постоянная Стефана-Больцмана;

А₁ - поглощательная способность зоны «i»;

s₀ = 5,67 * 10^-8 Вт/м²К⁴;

находим коэффициенты теплоотдачи излучением и яркостные температуры для всех расчетных зон контура.

4.6. Расчет температур продуктов сгорания на новом временном шаге производим при помощи теплового баланса.

4.7. Решая дифференциальное уравнение теплопроводности для каждой расчетной зоны футеровки колпака, находим температурное поле кладки на последующем шаге по времени.

4.8. На выходе из расчета теплообмена в наружном контуре имеем новые значения температур футеровки и продуктов сгорания, а также коэффициенты теплоотдачи излучением и конвекцией и яркостные температуры для расчетных зон на наружной поверхности муфеля.

5.   Рассчитываем теплообмен во внутреннем контуре:

5.1. По известным температурам муфеля и рулонов находим степени черноты и поглощательные способности для всех поверхностных расчетных зон контура.

5.2. Рассчитываем и нормируем матрицу угловых коэффициентов излучения.

5.3. Вычисляем коэффициенты теплоотдачи излучением и конвекцией, а также яркостные температуры для всех расчетных зон контура.

5.4. Рассчитываем тепловой баланс защитного газа на всех участках его циркуляции и находим температуры объемных зон.

5.5. Решая уравнение теплопроводности для рулонов, находим температурное поле садки на последующем шаге по времени.

5.6. Из теплового баланса дисков конвекторного кольца получаем их температуры на новом шаге по времени.

5.7. В результате расчета теплообмена во внутреннем контуре получаем температуры рулонов и защитного газа на последующем шаге по времени, а также коэффициенты теплоотдачи конвекцией и излучением и яркостные температуры для расчетных зон на внутренней поверхности муфеля.