Навигация
Исходные данные, основные требования и этапы проектирования
1. Исходные данные, основные требования и этапы проектирования
В комплексных заданиях на курсовой проект (работу) содержатся следующие исходные данные:
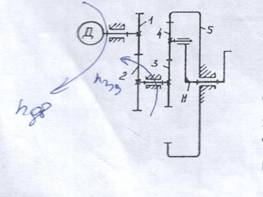
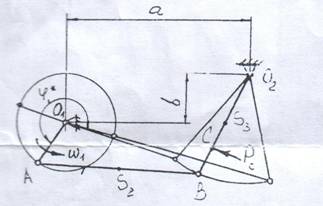
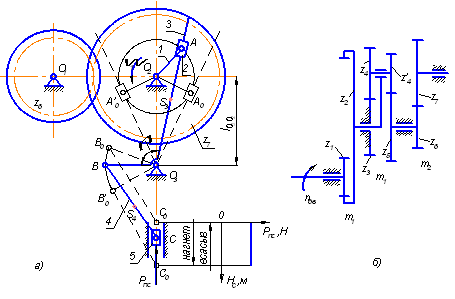
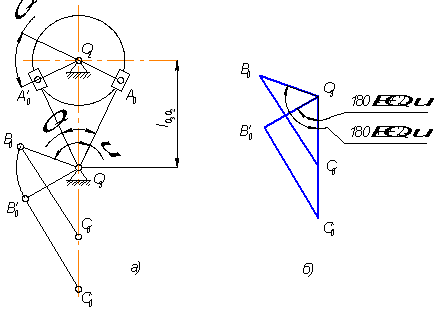
Структурная схема кулачкового механизма, показывающая характер взаимосвязей звеньев и их относительное расположение, тип кулачка, вид толкателя и характер его движения. Ведущим звеном в кулачковом механизме (рис. 1, 2) является дисковый кулачок 1, ведомым - толкатель 2, снабженный роликом 3. Толкатель может совершать поступательное (рис. 1) или вращательное (рис. 2) движение.
Максимальное перемещение толкателя - ход толкателя h (рис. 1, 2) или угол поворота толкателя b![]() (рис. 2)
(рис. 2)
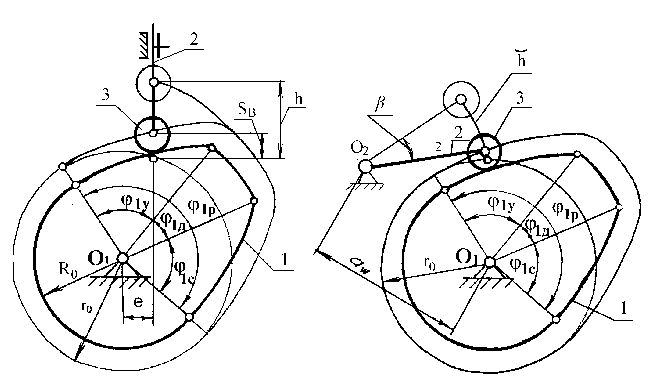
Рис.1 Рис.2
Длина толкателя ![]() 2в случае вращательно перемещающегося толкателя или внеосность е в случае поступательно движущегося толкателя.
2в случае вращательно перемещающегося толкателя или внеосность е в случае поступательно движущегося толкателя.
Фазовые углы: угол рабочего профиля кулачка ![]() и его составляющие - при удалении
и его составляющие - при удалении ![]() , при дальнем стоянии
, при дальнем стоянии ![]() , и сближении
, и сближении ![]() , которые назначаются в соответствии с циклограммой, отражающей согласованность перемещений исполнительных звеньев механизма.
, которые назначаются в соответствии с циклограммой, отражающей согласованность перемещений исполнительных звеньев механизма.
Закон движения толкателя в виде графика изменения ускорения толкателя в зависимости от угла поворота кулачка. Закон движения определяется конкретной технологической операцией, для выполнения которой предназначен проектируемый механизм.
Допустимый угол давления [J].
Направление вращения кулачка и частота его вращения в с-1.
При проектировании кулачковых механизмов необходимо соблюдать следующие основные требования:
проектируемый механизм должен обеспечивать заданный закон движения;
механизм должен иметь наименьшие габариты при достаточной надежности работы;
детали, составляющие механизм, должны быть технологичными, а их сборка - простой.
Проектирование кулачкового механизма делится на три основных этапа:
Определение кинематических передаточных функций, характеризующих изменение ускорения, скорости и перемещения толкателя, в функции времени или угла поворота кулачка.
Определение основных размеров кулачкового механизма - минимального радиуса кулачка ![]() , внеосности
, внеосности ![]() или межосевого расстояния
или межосевого расстояния ![]() w, при которых углы давления не превышают допустимых значений.
w, при которых углы давления не превышают допустимых значений.
Определение координат профиля кулачка.
Проектирование кулачкового механизма может быть выполнено графическим методом либо по аналитическим зависимостям с применением ЭВМ. В учебных целях при выполнении курсового проекта используют сочетание графических методов определения параметров кулачкового механизма с анализом математических моделей и выполнением расчетов на ЭВМ.
Применение графического метода позволяет предварительно изучить алгоритм реализации поставленной задачи, выявить связи между отдельными параметрами и сформировать математическую модель для составления программы расчета на ЭВМ. В итоге расчетов на ЭВМ студент получает таблицу результатов, которые ему следует проанализировать и сравнить с результатами графических построений и вычислений.
Выбор закона движения толкателя
При проектировании профиля кулачка обычно задаются законом движения толкателя. Выбор закона движения определяется главным образом теми требованиями, которые предъявляет технологический процесс к движению толкателя. В качестве требуемого закона движения можно принять определенный тип кривой перемещения, скорости или ускорения. Динамика кулачковых механизмов в основном определяется законами изменения ускорений (так как с ускорениями толкателя связаны пропорциональные им и массе толкателя силы инерции, учитывать которые приходиться при расчете замыкающих пружин, при определении напряжений в деталях механизма и т.д.), поэтому обычно в качества закона движения толкателя задаются кривой (или уравнением) относительных ускорений толкателя. Технологические соображения в большинстве случаев заставляют обращаться к сложным законам движения.
В табл. 1...5 приведены некоторые законы движения толкателя, представленные в виде безразмерных коэффициентов относительных значений ускорений ![]() и угла поворота Ку на фазе удаления. Коэффициент угла поворота Ку = j1р / jу меняется в пределах от 0 до I, а коэффициент ускорения в пределах
и угла поворота Ку на фазе удаления. Коэффициент угла поворота Ку = j1р / jу меняется в пределах от 0 до I, а коэффициент ускорения в пределах ![]() может изменяться по величине и по знаку. Для приведенных примеров вначале, а также в промежуточных положениях ускорение может изменяться скачком на конечную величину (мягкий удар за счет мгновенного изменения силы инерции). Для ряда законов ускорение меняется скачком в конце фазы удаления, в других случаях скачки на графиках ускорений могут отсутствовать.
может изменяться по величине и по знаку. Для приведенных примеров вначале, а также в промежуточных положениях ускорение может изменяться скачком на конечную величину (мягкий удар за счет мгновенного изменения силы инерции). Для ряда законов ускорение меняется скачком в конце фазы удаления, в других случаях скачки на графиках ускорений могут отсутствовать.
Кинематические характеристики кулачкового механизма при задании функций через безразмерные коэффициенты могут быть представлены на фазе удаления в следующем виде:
перемещение толкателя - ![]()
кинематическая передаточная функция скорости толкателя -
![]() ;
;
кинематическая передаточная функция ускорения толкателя
![]() .
.
Определение кинематических передаточных функций кулачкового механизма
Связь между
кинематическими
параметрами
толкателя -
ускорением
![]() ,
скоростью
,
скоростью
![]() и перемещением
и перемещением
![]() определяется
известными
соотношениями:
определяется
известными
соотношениями:
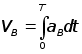 ,
,
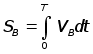 ,
,![]()
где Т - время одного оборота кулачка.
Так как закон
изменения
скорости кулачка
неизвестен,
приведенные
зависимости
нельзя использовать
непосредственно,
но их можно
выразить через
кинематические
передаточные
функции, которые
не зависят от
времени:![]()
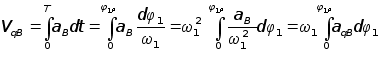 ,
,
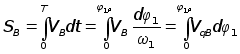 .
.
При расчете размеров и координат профиля кулачка кулачкового механизма определяющими являются ход толкателя, угол рабочего профиля кулачка и функциональная зависимость ускорения (относительного ускорения) толкателя от угла поворота кулачка. Если задать эту зависимость в аналитической форме, то последующим интегрированием могут быть получены зависимости кинематической передаточной функции скорости и перемещения толкателя.
Любую непрерывную
дифференцируемую
функцию вида ![]() можно представить
разложением
в ряд:
можно представить
разложением
в ряд:
![]() , (1)
, (1)
![]() . (2)
. (2)
(1) - полиномиальное разложение;
(2) - разложение в тригонометрический ряд;
![]() -
остаточный
член.
-
остаточный
член.
Двойное интегрирование выражений (1) и (2) позволяет получить
![]() , (3)
, (3)
![]() , (4)
, (4)
![]() , (5)
, (5)
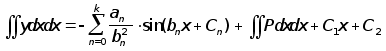 , (6)
, (6)
где С1 , С2 - константы интегрирования.
Если предположить
что
![]() ,
то интегралы
от Р из формул (3) ... (6) можно исключить.
Таким образом,
имея зависимости
,
то интегралы
от Р из формул (3) ... (6) можно исключить.
Таким образом,
имея зависимости ![]() вида (1) или (2), легко
получить
аналитические
зависимости
вида (1) или (2), легко
получить
аналитические
зависимости ![]() вида (3) или (4) и
зависимости
вида (3) или (4) и
зависимости ![]() вида (5) или (6).
вида (5) или (6).
В программе
QUL
реализован
алгоритм, вычисляющий
значения первого
и второго интеграла
относительного
ускорения
толкателя для
определения
углов поворота
кулачка. Следует
заметить что
![]() в общем виде
может иметь
точки разрыва.
При этом функция
в общем виде
может иметь
точки разрыва.
При этом функция ![]() при
при
![]() разбивается
на участки
разбивается
на участки
![]() ,
,
где ![]() -
индекс
участка (режима).
-
индекс
участка (режима).
Так что функция ![]() - кусочно-непрерывная
дифференцируемая
функция в области
своего определения
- кусочно-непрерывная
дифференцируемая
функция в области
своего определения ![]() ,
каждый
,
каждый ![]() - й участок
называется
режимом, при
этом
- й участок
называется
режимом, при
этом
![]()
Чтобы избежать
неопределенности
в задании функции
![]() ,
отрезки
,
отрезки ![]() открыты справа.
Для обеспечения
задания функции
на
открыты справа.
Для обеспечения
задания функции
на ![]() -
ом режиме
-
ом режиме
![]() предполагается,
что
предполагается,
что ![]() .
Требование
.
Требование
![]() не является
обязательным.
не является
обязательным.
Точность
интегрирования
определяется
не шагом по
углу поворота,
а точностью
задания функции
на участке,
т.е. величиной
![]() .
.
Если исходная функция заданна в виде графика или таблицы значений, то решение получают при помощи численных или графических методов. Для определения передаточной функции скорости толкателя интегрируют заданную функцию ускорения толкателя, интегрируя полученную функцию скорости, находят функцию перемещения толкателя. Обычно применяется численное интегрирование методом трапеций по формулам:
![]()
![]()
где - ![]() приращение
угла поворота
кулачка на шаге
интегрирования,
приращение
угла поворота
кулачка на шаге
интегрирования,
N - число равноотстоящих точек, в которых заданны значения переменной.
Примечание:
В течение цикла движения толкатель кулачкового механизма должен переместиться из начального положения на величину хода h , а затем возвратиться в исходное положение, то есть перемещение толкателя на фазе удаления равно перемещению на фазе сближения. Следовательно, график кинематической передаточной функции скорости должен удовлетворять условию:
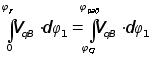 ,
,
где jсо-угловая координата начальной точки фазы сближения.
Скорость и кинематическая передаточная функция скорости толкателя на фазах ближнего и дальнего выстоя равны нулю. Чтобы эти условия выполнялись необходимо выполнить соотношения
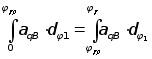 ,
,
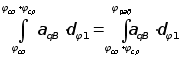 ,
,
где jyp- угловое перемещение при разгоне на фазе удаления;
jср - угловое перемещение при разгоне на фазе сближения;
jст = jраб - (jсо + jср)- угловое перемещение при торможении на фазе сближения.
Эти условия необходимо учитывать при построении безразмерных графиков передаточной функции скорости и передаточной функции ускорения, выравнивая соответствующие указанным интегралам площади над осью абсцисс и под ней.
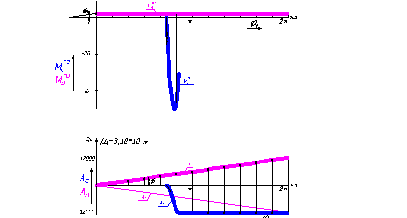
При работе
над листом
проекта с
использованием
графического
интегрирования
(рис. 3) все три
графика располагают
один под другим
на одинаковой
базе по оси
абсцисс, которую
удобно выбирать
в пределах
150...240 мм. График
скорости ![]() толкателя (рис.
3б) получается
(строится) методом
графического
интегрирования
из графика
ускорения
толкателя. Для
этого на продолжении
оси t
графика ускорений
с левой стороны
выбирается
отрезок интегрирования
К1
=30...50 мм. После
построения
графика скорости
строится график
перемещений
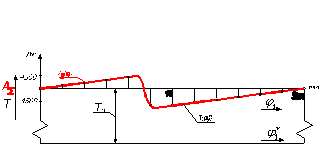
толкателя рис.
3в. Для этого
также на продолжении
оси абсцисс
t
графика
толкателя (рис.
3б) получается
(строится) методом
графического
интегрирования
из графика
ускорения
толкателя. Для
этого на продолжении
оси t
графика ускорений
с левой стороны
выбирается
отрезок интегрирования
К1
=30...50 мм. После
построения
графика скорости
строится график
перемещений
толкателя рис.
3в. Для этого
также на продолжении
оси абсцисс
t
графика
![]() откладывается
отрезок интегрирования
К2.
Можно принимать
К1
= К2. Или
принять их
равными mj.
В зависимости
от принятых
отрезков
интегрирования
на графике
откладывается
отрезок интегрирования
К2.
Можно принимать
К1
= К2. Или
принять их
равными mj.
В зависимости
от принятых
отрезков
интегрирования
на графике ![]() ордината
ордината
![]() получается
больше или
меньше. Если
частота вращения
кулачка
n1
(с-1)
и максимальное
перемещение
(ход) толкателя
h
в исходных
данных на проект
заданы, то можно
определить
следующие
масштабы:
получается
больше или
меньше. Если
частота вращения
кулачка
n1
(с-1)
и максимальное
перемещение
(ход) толкателя
h
в исходных
данных на проект
заданы, то можно
определить
следующие
масштабы:
Масштаб
времени, мм
/ c ![]() , (7)
, (7)
Масштаб
перемещений,
мм
/ м ![]() , (8)
, (8)
Масштаб
скорости, мм
/ мс-1![]() (9)
(9)
Масштаб
ускорений, мм
/ мс-2![]() (10)
(10)
где ![]() -
максимальная
ордината с
графика перемещений
точки В
центра ролика
толкателя, мм;
-
максимальная
ордината с
графика перемещений
точки В
центра ролика
толкателя, мм;
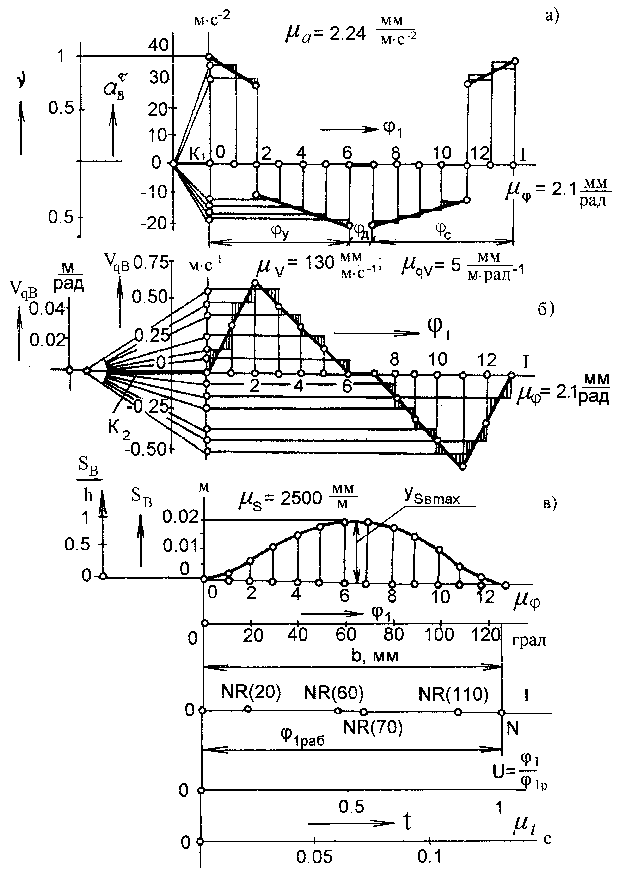
Рис.3
![]() - угол рабочего
профиля кулачка
в градусах;
- угол рабочего
профиля кулачка
в градусах;
![]() -
база
графика, мм;
-
база
графика, мм;
![]() -
частота
вращения кулачка,
c-1.
-
частота
вращения кулачка,
c-1.
Если в задании
на проект значение
угловой скорости
или частоты
вращения кулачка
не заданы , то
можно интегрировать
заданный график
по углу поворота
кулачка ![]() и получить
графики кинематических
передаточных
функций. Для
перехода от
вычисленных
интегралов
и получить
графики кинематических
передаточных
функций. Для
перехода от
вычисленных
интегралов
![]() и
и ![]() к действительным
значениям
кинематической
передаточной
функции скорости
к действительным
значениям
кинематической
передаточной
функции скорости
![]() и перемещения
и перемещения
![]() определяются масштабы, которые
вычисляются
с учетом заданного
максимального
перемещения
( хода ) толкателя
h
и максимального
вычисленного
перемещения
определяются масштабы, которые
вычисляются
с учетом заданного
максимального
перемещения
( хода ) толкателя
h
и максимального
вычисленного
перемещения
![]() из массива
перемещений
из массива
перемещений
![]() .
.
Масштаб угла
поворота, мм
/ рад ![]() , (11)
, (11)
Масштаб передаточной функции
скорости
,мм
/ м рад-1
, ![]() , (12)
, (12)
Масштаб передаточной функции
ускорения,
мм
/ м рад-2, 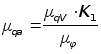 , (13)
, (13)
где ![]() - угол
рабочего профиля
кулачка в радианах,
- угол
рабочего профиля
кулачка в радианах,
К1 ,К2 - отрезки интегрирования, мм.
В массиве
![]() отыскиваются
максимальное
отыскиваются
максимальное
![]() и минимальное
и минимальное
![]() значения и
соответствующие
им углы
значения и
соответствующие
им углы
![]() и перемещения
толкателя
и перемещения
толкателя ![]() .
.
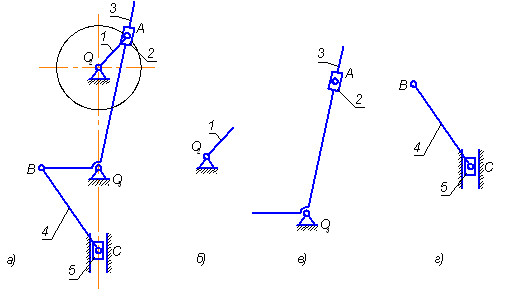
4. Определение основных размеров кулачкового механизма из условия ограничения угла давления
При выборе
основных размеров
кулачкового
механизма -
минимального
радиуса кулачка ![]() ,
смещения
оси толкателя
относительно
оси вращения
кулачка
,
смещения
оси толкателя
относительно
оси вращения
кулачка ![]() или расстояния
между осями
вращения кулачка
и толкателя
или расстояния
между осями
вращения кулачка
и толкателя ![]() w,
стремятся
получить минимально
возможные
значения углов
давления
w,
стремятся
получить минимально
возможные
значения углов
давления ![]() , т.к. при
этом уменьшаются
реакции в
кинематических
парах, величина
вращающего
момента на валу
кулачка, силы
трения;
повышается
КПД и надежность
механизма
, т.к. при
этом уменьшаются
реакции в
кинематических
парах, величина
вращающего
момента на валу
кулачка, силы
трения;
повышается
КПД и надежность
механизма
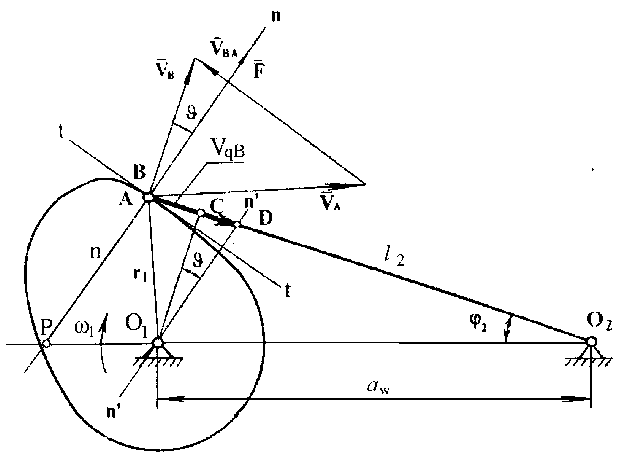
Рис. 4
Углом давления
называется
угол между
вектором силы,
действующим
на ведомое
звено со стороны
ведущего звена,
и вектором
скорости точки
приложения
этой силы. Связь
угла давления
с характером
движения звеньев
высшей кинематической
пары и основными
размерами
механизма может
быть установлена
с использованием
рис. 4 . Угол давления
заключен между
направлением
вектора силы
F,
действующей
со стороны
кулачка на
толкатель по
нормали nn,
проведенной
в точке касания
звеньев, и
направлением
вектора скорости
точки В
-
VB
,
принадлежащей
толкателю,
перпендикулярного
толкателю. Угол
CO1D
равен
углу давления ![]() , и
, и
![]()
Из подобия треугольника плана скоростей и треугольника BO1D
![]()
![]()
![]() и
и 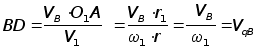
![]()
![]()
После подстановки значений отрезков зависимость между углом давления и кинематическими параметрами механизма приобретет вид:
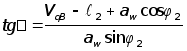 , (14)
, (14)
где ![]() -
передаточная
функция скорости
точки В
толкателя;
-
передаточная
функция скорости
точки В
толкателя;
![]() - расстояние
между осями
вращения кулачка
и толкателя;
- расстояние
между осями
вращения кулачка
и толкателя;
![]() 2
- длина толкателя;
2
- длина толкателя;
![]() - угол, определяющий
положение
толкателя
относительно
линии межосевого
расстояния.
- угол, определяющий
положение
толкателя
относительно
линии межосевого
расстояния.
В случае, когда толкатель совершает прямолинейно-поступательное движение, выражение для определения угла давления имеет вид [2] :
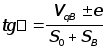 , (15)
, (15)
где ![]() -
смещение
направляющей
толкателя
относительно
оси вращения
кулачка,
-
смещение
направляющей
толкателя
относительно
оси вращения
кулачка,
![]() -
координата
точки В
толкателя в
системе координат,
имеющих начало
на оси вращения
кулачка.
-
координата
точки В
толкателя в
системе координат,
имеющих начало
на оси вращения
кулачка.
Величины ![]() ,
,
![]() и
и ![]() , входящие в
формулу для
определения
, входящие в
формулу для
определения ![]() , являются
переменными.
Следовательно,
угол давления
также является
переменной
величиной и
его текущие
значения
, являются
переменными.
Следовательно,
угол давления
также является
переменной
величиной и
его текущие
значения ![]() i
не должны
превосходить
определенный
допустимый
угол давления
i
не должны
превосходить
определенный
допустимый
угол давления
Ji
Похожие работы
... φу=100 град; φдс=40 град; φв=70 град; Ход толкателя кулачкового механизма h=74мм; Эксцентриситет e =28 мм; Тип диаграммы 2 1 СИНТЕЗ ЗУБЧАСТОГО РЕДУКТОРА 1.1 Расчет геометрических параметров зубчатой передачи 1-2 Проектируем зацепление со смещением 1 – 2. Основними исходными данными ...
... рассчитанными длинами звеньев вычерчен на листе №1 формата А1. 2.2 Построение графика силы сопротивления Механическая характеристика, т.е. зависимость силы сопротивления от перемещения верхнего ножа аллигаторных ножниц строится по диаграмме усилия реза, представленной на рис.1б: сначала по заданной координате находится положение разрезаемого металла (точка К) и в масштабе вычерчивается его ...
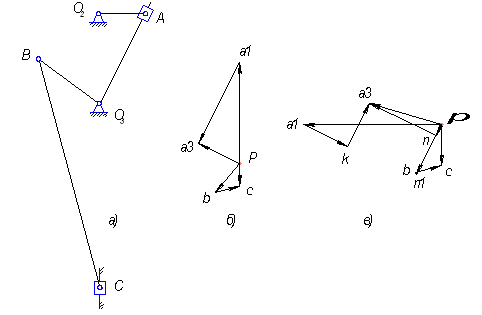
анов. Особенностью поршневых насосов является периодический, пульсирующий характер подачи, обуславливающий неравномерность давлений и подачи по времени. Для поршневых насосов наряду с кривошипно-ползунными механизмами для увеличения производительности применяются кулисные механизмы. В задании поршневой насос состоит из кулисного О2АО3 и шатунного ОВС механизмов (рис. 1а). На ведущий вал О2 ...
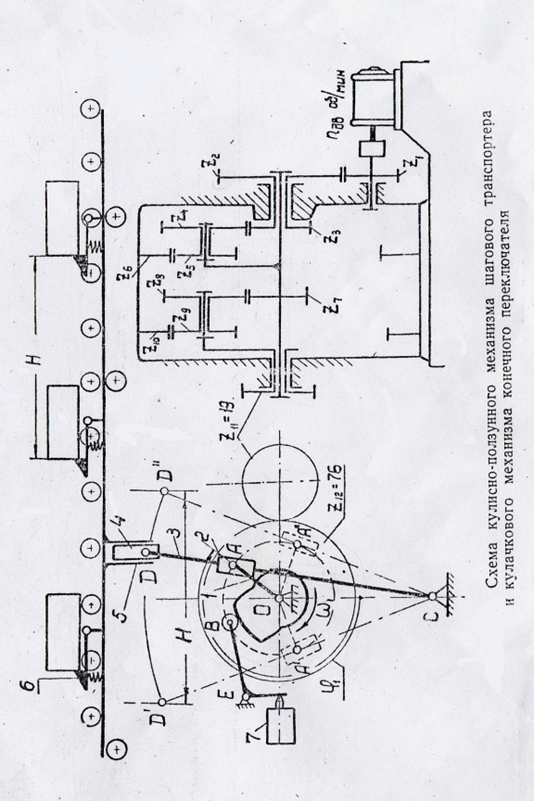
... При графическом изображении физических величин масштаб обозначается буквой с индексом, указывающим, к какой величине он относится. 1. Проектирование основного механизма и определение закона движения 1.1 Проектирование механизма по заданным условиям Механизм шагового транспортера автоматической линии вычерчен в масштабе =50мм/м. Положения начального звена 1 при вращении вокруг центра О ...

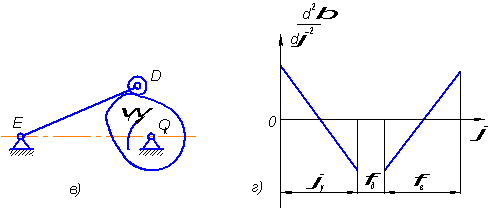
0 комментариев