Интерферометры
Звездный интерфероментр Майкельсона
Интерферометр Фабри-Перо
Дифракционная решетка
Дифракция на круглом отверстии
Обсуждение полученных результатов
Пятно Пуассона
Одноосные кристаллы
Двойное лучепреломление
Естественное вращение плоскости поляризации
Искусственное двойное лучепреломление
Тепловое излучение
Плотность лучистой энергии
Формула Планка
Оптическая пирометрия
Теплоемкость кристаллической решетки
Эффект Допплера
Фотоны
Примеры использования понятия фотона
Эффект Комптона
Примеры использования понятия фотона
Эффект Комптона
Физический смысл волновой функции
Как нам это понимать
Парадокс Больцмана
Нормирование волновой функции
Стоячие волны. Рефракция
Квантование момента импульса
Навигация
Интерферометр Фабри-Перо
Лекции по физике
143609
знаков
73
таблицы
14
изображений
8.6.5 Интерферометр Фабри-Перо.
Угловое распределение амплитуды проходящей волны
| d
q q
1 2 3 4 |
На своем пути каждый последующий из пронумерованных лучей испытывает два дополнительных отражения от внутренних поверхностей пластин. Стало быть, их интенсивности различаются в r2 раз. Интенсивность пропорциональна квадрату амплитуды и поэтому
; 
.
Далее, разность оптических путей соседних лучей равняется 
и разность фаз их колебаний в удаленной точке наблюдения
.
Таким образом, для амплитуды суммарных колебаний мы имеем выражение:
.
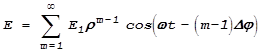Начальную фазу колебаний первого луча мы положили равной нулю.
Для сложения этих колебаний перейдем к комплексным переменным - добавим мнимую часть, памятуя, что физический смысл имеет лишь реальная часть суммы, которую мы получим:
.
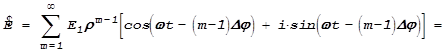
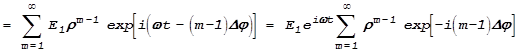Итак, нам надо найти сумму членов бесконечной геометрической прогрессии, знаменатель которой 
. Таким образом,
.
Амплитуда суммарных колебаний равна модулю комплексного значения 
:
.
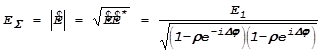Воспользовавшись формулой Эйлера, произведем перемножение скобок под квадратным корнем в знаменателе:
.
| r: ES
0,05
0,25
0,75 0 q |
Вспомним, что
|
|
.
Таким образом,
.
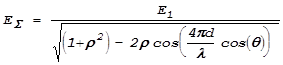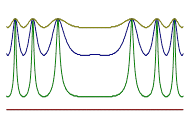
Как и ожидалось, с увеличением коэффициента отражения глубина минимумов увеличивается. Одновременно уменьшается ширина интерференционных полос. Предвидеть этот результат было не так просто.
9. Дифракция Фраунгофура
Дифракция рассматривает процессы отклонения направления распространения света от прямолинейного при встрече с некоторыми препятствиями или при отражении от них. В случае дифракции Фраунгофера рассматривается падение на препятствие плоской волны (бесконечно удаленный источник света) и подразумевается, что зона наблюдения удалена от препятствия на достаточно большое расстояние (находится на бесконечности). Коротко говоря, это “дифракция в параллельных лучах”.
Как Вы увидите, основные задачи дифракции Фраунгофера мы, собственно, уже решили. Просто мы говорили о волнах вообще, а словом дифракция обычно обозначают именно оптические явления, поведение в том или ином случае световой (электромагнитной) волны.
9.1. Дифракция на щели
Ранее мы получили такое выражение для углового распределения амплитуды от системы точечных источников, от “цепочки” источников длиной b:
.
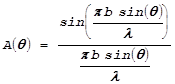Ввиду особой важности да и сложности понимания этого результата получим его еще раз - другим способом.
| X
b
0 q |
В связи с рассмотрением явлений дифракции формулируется принцип Гюйгенса-Френеля. Согласно этому принципу элементарный участок волнового фронта считается точечным источником вторичных волн, огибающая которого и является “новым” фронтом волны. В случае дифракции на щели в качестве таких источников выбираются узкие полоски (вдоль щели), которые являются источниками цилиндрических когерентных волн. Электромагнитные колебания в удаленной зоне наблюдения подсчитывается как сумма колебаний волн, пришедших от таких источников.
На этот раз мы проведем их сложение с помощью векторной диаграммы. Амплитуда вторичной волны пропорциональна ширине элементарной полоски: 
, а начальная фаза колебаний зависит от координаты выбранной полоски: 
. Таким образом, разность фаз колебаний от соседних элементарных полосок шириной Dx составит 
. На такой угол будут повернуты по отношению друг к другу соответствующие векторы на фазовой диаграмме.
|
R Dj j Dj DE0 |
ESПри стремлении ширины полоски Dx к нулю образованная элементарными векторами ломаная превращается в дугу окружности радиуса R, угловой размер дуги
.
При изменении угла q угловые размеры дуги изменяется. Но длина дуги, равная сумме модулей (длин) элементарных векторов, считается постоянной:
.
Это позволяет нам определить радиус дуги и амплитуду суммарных колебаний (см. рисунок) при произвольном q:
; 
.
Как видите, мы получили то же выражение, что и раньше. Но векторная диаграмма позволяет нам нагляднее представить причины обращения амплитуды суммарных колебаний в нуль и достижение максимумов.
При j=2p дуга превращается в окружность, амплитуда суммарных колебаний равна нулю. Максимумы достигаются при j=0 и, (приблизительно) при j=(2k+1)p.
|
1 2 ES 3
ES= E0
ES=0 |
Эти ситуации показаны на рисунке. При q=0 все элементарные векторы лежат на прямой, амплитуда суммарных колебаний максимальна и равна E0. По мере увеличения угла наблюдения q и, соответственно, угла j амплитуда колебаний уменьшается и при j=2p обращается в нуль. Затем дуга скручивается в спираль и максимум достигается приблизительно в тот момент, когда она представляет собой полторы окружности (2, j=3p). При этом амплитуда колебаний равна примерно диаметру окружности: 
. Затем спираль становится “двойной окружностью”, амплитуда колебаний снова обращается в нуль (3) и т.д.
Похожие работы
... свойства. А.у.т. - тело, для которого силы однозначно определяют деформации и наоборот. Правильность выбранной абстракции подтверждается совпадением, определенной точностью результатов теории и опыта. Физика - наука, устанавливающая закономерные связи посредством наблюдений явлений в природе и посредством лабораторных опытов. Согласие результатов научного анализа с результатами опыта - критерий ...
... так, как большинство материалов относится к устному творчеству, откуда и были получены, также есть выдержки из книг: «Физики шутят», «Физики продолжают шутить», «Сборник задач по физике» Г. Остера. Шутки, которые шутят физики. Один математик спросил коллегу, известного своими религиозными убеждениями: - Вы, что же, верите в единого ...
... фара́да). 1 фарад равен электрической ёмкости конденсатора, при которой заряд 1 кулон создаёт между обкладками конденсатора напряжение 1 вольт. Ф = Кл/В = A·c/B Единица названа в честь английского физика Майкла Фарадея Фарад — очень большая ёмкость. Емкостью 1Ф обладал бы уединенный шар, радиус которого был бы равен 13 радиусам Солнца. Для сравнения, ёмкость Земли (шара размером с ...
... гальванометра отклонялась (то же происходило и при поднятии электромагнита из катушки). Эта схема напоминает рисунок из лабораторного журнала Фарадея. Удивительно, как схожи оказались эксперименты двух великих физиков, работавших независимо друг от друга на разных континентах! В своей статье, написанной уже после знакомства с опытом Фарадея, Генри, отдавая должное английскому физику, подчеркнул, ...
0 комментариев