Коэффициент удельного веса заемных средств в активе

2.2. Коэффициент удельного веса заемных средств в активе.

1993 г.

1994 г. 

1995 г.

 

2.3. Коэффициенты заемных и собственных средств.

1993 г.

1994 г. 

1995 г.

3. Расчет показателей оборачиваемости

3.1. Коэффициенты оборачиваемости активов.

1994 г.

1995 г. 

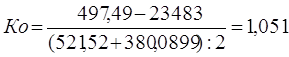
3.2. Коэффициенты оборачиваемости собственного капитала.

1994 г.

1995 г. 

3.3. Фондоотдача

1994 г.

1995 г. 

3.4. Коэффициенты оборачиваемости запасов.

1994 г.

1995 г. 

3.5. Показатели оборачиваемости запасов в днях

1994 г.

1995 г. 

3.6. Коэффициент оборачиваемости дебиторской задолженности.

1994 г.

1995 г. 

3.7.Коэффициент оборачиваемости кредиторской задолженности.

1994 г.

1995 г. 

4.Расчет показателей рентабельности.

4.1. Рентабельность всего капитала, %.

1994 г.

1995 г. 

4.2. Чистая рентабельность всего капитала, %.

1994 г.

1995 г. 

4.3.Чистая рентабельность собственного капитала.

1994 г.

1995 г. 

4.4.Рентабельность инвестиций.

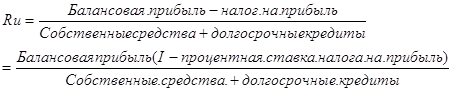
1994 г.

1995 г. 

4.5.Чистая рентабельность оборота, %.

1994 г.

1995 г. 

Приложение 3.

Оценка рыночной стоимости фирмы методом дисконтированных

денежных потоков.

Вариант 1.

Таблица 1.

№	Вид продукции, услуг	Базовый 1995 г.	Годы					Постпрогнозныйпериод
			1996	1997	1998	1999	2000
1.	Реализация лыж	100	+10	+15	+20	+15	+10	+5
2.	Реализация хоккейных клюшек	100	+7	+7	+7	+5	+5	+5
3.	Доходы от сдачи в аренду	100	0	+40	+40	+30	+10	+5

Таблица 2.

Износ по зданиям, сооружениям, оборудованию и капитальным вложениям будущих периодов, тыс.ам.долл.

№	Вид продукции, услуг	Годы					Постпрогнозныйпериод
		1996	1997	1998	1999	2000
1.	Существующие здания и сооружения	12,1	12,1	12,1	12,1	12,1	12,1
2.	Существующее оборудование	4,4	4,4	4,4	4,4	4,4	4,4
3.	Капитальные вложения 1996 г.	11,5	11,5	11,5	11,5	11,5	11,5
4.	Капитальные вложения 1997 г.	0	6,9	6,9	6,9	6,9	6,9
5.	Всего	28	34,9	34,9	34,9	34,9	34,9

Приложение 3.

Таблица 3.

Прогноз будущих доходов, ты.ам.долл.

Вид продукции, услуг	Базов 1995г.	Годы					Постпрогнозныйпериод
		1996	1997	1998	1999	2000
Лыжи Выручка от реализации	280,92	309,00	355,37	426,44	490,40	539,44	566,40
Издержки, (70 %)	196,64	216,30	248,76	298,50	343,30	377,60	396,50
Валовая прибыль	84,28	92,7	106,61	127,94	147,10	161,84	169,90
Хоккейные клюшки Выручка от реализации	144,58	154,70	165,52	177,12	186,0	195,27	205,00
Издержки, (60 %)	93,97	100,55	107,59	115,13	120,9	126,90	133,25
Валовая прибыль	50,61	54,15	57,93	61,99	65,1	68,37	71,75
Доходы от сдачи в аренду Затраты на содержание (30 %)	0	20,7	29,0	40,57	52,74	58,0	61,0
Валовая прибыль	0	48,3	67,6	94,67	123,07	135,4	142,0
Всего выручки от реализации	425,5	532	617,49	738,8	852,21	926,11	974,4
Всего валовая прибыль	134,89	195,15	232,14	284,6	335	365,61	383,65

Таблица 4.

Расчет денежного потока, тыс.ам.долл.

Показатель	Годы					Постпрогнозныйпериод
	1996	1997	1998	1999	2000
Валовая прибыль	195,15	232,14	284,6	335,27	364,61	383,65
Административные издержки (10% от валовой прибыли)	19,51	23,21	28,5	33,52	36,56	38,36
Процент за кредит (20%)	40,0	29,011	15,82	-	-	-
Налогооблагаемая прибыль	135,64	179,92	240,28	301,72	329,05	345,29
Налог на прибыль (35%)	47,48	62,97	84,1	105,61	115,17	102,85
Чистая прибыль	88,16	116,95	156,18	196,14	213,88	224,44
Начисленный износ	28,0	34,90	34,90	34,90	34,90	34,90
Прирост долгосрочной задолженности	0	0	0	0	0	0
Прирост чистого оборотного капитала	24,66	19,50	27,90	26,08	17,46	10,65
Капитальные вложения	115,0	69,0	0	0	0	0
Денежный поток	176,5	63,35	163,18	204,96	231,32	248,69
Коэффициент текущей стоимости	0,769	0,591	0,455	0,350	0,269	0,207
Текущая стоимость денежных потоков	135,73	37,44	74,25	71,74	62,23	51,47
Сумма текущей стоимости денежных потоков	432,86
Выручка от продажи фирмы в конце последнего прогнозируемого года
Текущая стоимость выручки от продаж фирмы	994,76 * 0,269 = 267,59
Рыночная стоимость собственного капитала фирмы	432,86 + 267,59 = 700,45
Недостаток стоимость собственного капитала фирмы	532,7 * 0,2645 – 37,74 = 103,16
Рыночная стоимость собственного капитала после внесения поправок	700,45 – 103,16 = 597,29

Приложение 4.

Вариант 2.

Таблица 1.

Темпы прироста объемов продаж в прогнозный период по сравнению с предшествующим годом, %.

№	Вид продукции, услуг	Базовый 1995 г.	Годы					Постпрогнозныйпериод
			1996	1997	1998	1999	2000
1.	Реализация лыж	100	+8	+12	+17	+10	+7	+3
2.	Реализация хоккейных клюшек	100	+6	+6	+6	+5	+5	+3
3.	Доходы от сдачи в аренду	100	0	0	0	0	0	0

Таблица 2.

Износ по зданиям, сооружениям, оборудованию и капитальным вложениям будущих периодов, тыс.ам.долл.

№	Вид продукции, услуг	Годы					Постпрогнозныйпериод
		1996	1997	1998	1999	2000
6.	Существующие здания и сооружения	12,1	12,1	12,1	12,1	12,1	12,1
7.	Существующее оборудование	4,4	4,4	4,4	4,4	4,4	4,4
8.	Капитальные вложения 1996 г.	11,5	11,5	11,5	11,5	11,5	11,5
9.	Капитальные вложения 1997 г.	0	6,9	6,9	6,9	6,9	6,9
10.	Всего	28	34,9	34,9	34,9	34,9	34,9

Приложение 3.

Таблица 3.

Прогноз будущих доходов, ты.ам.долл.

Вид продукции, услуг	Базов 1995г.	Годы					Постпрогнозныйпериод
		1996	1997	1998	1999	2000
Лыжи Выручка от реализации	280,92	309,00	355,37	426,44	490,40	539,44	566,40
Издержки, (70 %)	196,64	216,30	248,76	298,50	343,30	377,60	396,50
Валовая прибыль	84,28	92,7	106,61	127,94	147,10	161,84	169,90
Хоккейные клюшки Выручка от реализации	144,58	154,70	165,52	177,12	186,0	195,27	205,00
Издержки, (60 %)	93,97	100,55	107,59	115,13	120,9	126,90	133,25
Валовая прибыль	50,61	54,15	57,93	61,99	65,1	68,37	71,75
Доходы от сдачи в аренду Затраты на содержание (30 %)	0	20,7	29,0	40,57	52,74	58,0	61,0
Валовая прибыль	0	48,3	67,6	94,67	123,07	135,4	142,0
Всего выручки от реализации	425,5	532	617,49	738,8	852,21	926,11	974,4
Всего валовая прибыль	134,89	195,15	232,14	284,6	335	365,61	383,65

Таблица 4.

Расчет денежного потока, тыс.ам.долл.

Показатель	Годы					Постпрогнозныйпериод
	1996	1997	1998	1999	2000
Валовая прибыль	195,15	232,14	284,6	335,27	364,61	383,65
Административные издержки (10% от валовой прибыли)	19,51	23,21	28,5	33,52	36,56	38,36
Процент за кредит (20%)	40,0	29,011	15,82	-	-	-
Налогооблагаемая прибыль	135,64	179,92	240,28	301,72	329,05	345,29
Налог на прибыль (35%)	47,48	62,97	84,1	105,61	115,17	102,85
Чистая прибыль	88,16	116,95	156,18	196,14	213,88	224,44
Начисленный износ	28,0	34,90	34,90	34,90	34,90	34,90
Прирост долгосрочной задолженности	0	0	0	0	0	0
Прирост чистого оборотного капитала	24,66	19,50	27,90	26,08	17,46	10,65
Капитальные вложения	115,0	69,0	0	0	0	0
Денежный поток	176,5	63,35	163,18	204,96	231,32	248,69
Коэффициент текущей стоимости	0,769	0,591	0,455	0,350	0,269	0,207
Текущая стоимость денежных потоков	135,73	37,44	74,25	71,74	62,23	51,47
Сумма текущей стоимости денежных потоков	432,86
Выручка от продажи фирмы в конце последнего прогнозируемого года
Текущая стоимость выручки от продаж фирмы	994,76 * 0,269 = 267,59
Рыночная стоимость собственного капитала фирмы	432,86 + 267,59 = 700,45
Недостаток стоимость собственного капитала фирмы	532,7 * 0,2645 – 37,74 = 103,16
Рыночная стоимость собственного капитала после внесения поправок	700,45 – 103,16 = 597,29

 

Глава 2. ОЦЕНКА ФИНАНСОВЫХ (ПОРТФЕЛЬНЫХ) ИНВЕСТИЦИЙ. 2.I. Виды ценных бумаг.

Вложение денежных средств в ценные бумаге является одной, из форм финансовых инвестиций как для частного, так и институционального инвестора.

Получение дохода от вложения финансовых средств в ценные бумаги является главной, но не единственной целью. Так например, инвестиции в акции, кроме получения дохода в виде дивидендов, преследуют цель сохранении капитала в условиях инфляции, обеспечение прироста капитала за счет повышения курсовое стоимости акций и, наконец, институциональный инвестор может преследовать цель по реализации, так называемого, стратегического инвестирования, т.е. приобретения контрольного пакета акций с целью получения возможности управления компанией, эмитировавшей данные акции.

Bсe ценные бумаги, исходя ив их экономической природы, можно разделить на следующие группы: ценные бумаги, выражающие отношения совладения; ценные бумаги, опосредующие кредитные отношения; производные ценные бумаги.

К ценным бумагам, выражающим отношения совладения, или долевым ценным бумагам относятся акции.

К ценным бумагам, опосредующим кредитные отношения, относятся различные формы долговых обязательств: облигации, казначейские векселя и др.

К производным инструментам фондового рынка (производным ценным бумагам) относятся обратимые облигации (например, облигации, которые спустя определенное время могут быть обменены на акции), обратимые привилегированные акции (привилегированные акции, которые в некоторый период времени обмениваются на обыкновенные акции) и некоторые другие инструменты.

Исходя из механизма выплаты доходов, различаются ценные бумаги фиксированным доходом и ценные бумаги с изменяющимися доходом. Обычно твердый фиксированный процентный доход приносят облигации и ряд других долговых инструментов. Вместе с тем, фиксированные доходы выплачиваются и по привилегированным акциям. Как видим, разделение ценных бумаг по методу выплаты доходов не всегда совпадает с их классификацией по экономической природе.

Основную долю в общем объеме ценных бумаг составляют акции и облигации.

Перейдем к рассмотрению методов определения их цены и доходности.

2.2. Акции и определение их доходности.

Акции не относятся к ценным бумагам с фиксированным доходом Исключение составляют привилегированные акции, которые приносят фиксированный доход независимо от прибыли, полученной акционерным обществом, а при его ликвидации сродства, вложенные в привилегированные акции, возмещают по номиналу в первоочередном порядке.

В результате отсутствия гарантированного дохода эффективности операции с обыкновенными акциями может быть прогнозируема лишь условно. Поэтому риск инвестора, вложившего свой капитал в "обыкновенные" акции, выше, чем риск вложения в облигации или привилегерованные акции. При этом под риском будем понимать неопределенность в получении будущих доходов, т.е. возможность возникновения убытков или получения доходов, размеры которых ниже прогнозируемой. Величина получаемых дивидендов, а также разница в цене покупки и продажи являются двумя составляющими, которые определяют доход по акциям.

Эффективность инвестиций в акции выразим относительной величиной, которую можно записать в следующем виде:

где Р₀ - цена покупки акции;

Р₁ - цена продажи;

d - дивиденды, полученные за время владения акцией.

На цену акции влияет множество факторов, среди которых наиболее существенным является предполагаемый размер дивидендных выплат. К прочим факторам относятся: доверие к корпорации, эмитировавшей акции, прогнозирование ее дальнейшего развития, уровень рыночное ссудного процента и т.д.

При определении цены акции исходят из двух предположений:

I) с некоторой степенью вероятности можно предсказать ожидаемый размер дивидендов по акциям в текущем году (d₁), а такхе в ряд последующих лет (d₂, d₃… d_t).

2) акция будет бессрочно находиться на руках у ее владельца или его потомков, т.е. не будет продана. В этом случае расчетную цену акции Р можно определить как сумму приведенных стоимостей ежегодно приносимых акцией дивидендов при заданной ожидаемой доходности от их капитализации (реинвестирования) по ставке i.

Теоретически цена акции ( Р ) будет равна современной величине вечной ренты.

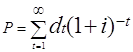
где d_t - дивиденд, выплачиваемый в t году.

i-          ставка процентов, учитываемая при оценивании.

Как правило, эта ставка весьма близка к средней ссудной ставке на рынке капиталов.

Если предположить, что дивиденды постоянны, т.е d_t = d_t+1…= d= const, то

Можно доказать равенство двух величин:

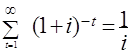, откуда следует, что

Таким образом, теоретическая цена акции прямо пропорциональна дивиденду но ней и обратно пропорциональна ставке процента, учитываемого при оценивании.

Если все же предположить, что через п лет акция будет продана, то цена акции будет равна сумме приведенных величин потока дивидендов и цены реализации, т.е.

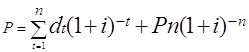
где Pn - цена реализации акции.

Оценка акций по приведенным формулам носит весьма условный характер, так как величины, входящие в них - дивиденды и уровень одного процента (i) является труднопредсказуемыми.

Вместе с тем уровень реальных цен складывается под влиянием прогнозных оценок, которые исходят из имеющейся информации о продуктивности каждой корпорации, ее дивидендной политики, а также расчеты эффективности альтернативных вложений.

2.3. Формирование портфеля акций и оценка его доходности.

Формируя инвестиционный портфель (портфель акций), инвесторы пытаются при минимальном риске получить максимальную прибыль. Достижение этой цели возможно только при принятии компромиссного решения, уравновешивающего эти факторы.

Создание оптимальной структуры инвестиционного портфеля зависит от звания ситуации на фондовом рынке и возможности ее прогнозирования.

(r_m1, r_m2, … r_mk) и (r_i1, r_i2, … r_ik)

Используя эти данные, можно рассчитать средние арифметические величины показателей эффективности акций, т.е. `r<sub>m</sub> и `r_i, а также среднестатистические отклонения этих показателей.

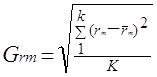(2.7.)

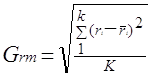(2.8.)

Дадим интерпретацию этим показателям. На протяжении рассматри­ваемого периода в К лет (месяцев, кварталов) доходность по рынку акций в целом и по отдельным акциям в каждом году (месяце) была близка к показателям `r<sub>m</sub> и `r_i, , т.е. к средним значениям доходно­сти. Однако в силу воздействия различных причин (факторов) показа­тели доходности отклонялись в ту или другую сторону от средних зна­чений. Можно предположить, что эти причины будут действовать и в будущем.

Величину фактического отклонения (вариацию) показателей эффек­тивности мы измерили с помощь» статистического показателя вариации - среднего квадратического отклонения (2.7; 2.8).

В случаях, когда вариация эффективности равна нулю (`r<sub>m</sub> = r<sub>m</sub> и `r_i = r_i,), показатель эффективности не отклоняется от сво­его среднего значения, т.е. нет неопределенности, а значит и риска. Чем больно вариация, тем больше и величина среднего квадратического отклонения, т.е. выше неопределенность и риск. Поэтому можно счи­тать величину G- мерой риска.

Предположим, инвестору предложены два вида ценных бумаг с пара­метрами `R<sub>i</sub> >`R_Y, а G_i<G_y, т.е. доходность i бумаг больше, чем y, а риск меньше. Естественно, грамотный инвестор, не­сомненно, выберет бумаги с показателем эффективности R_i .

Если эти параметры будут соотноситься, как R_i =`R_Y, а G_i>G_y инвестор выберет бумаги с показателем эффективности R_Y,

Инвестиции в ценные бумаги всегда сопровождаются необходи­мостью решения дилеммы: вкладывать деньги в акцию с большим доходом и большим риском или довольствоваться меньшим доходом, но и меньшим риском. Выбор варианта зависит от характера инвестора, суммы инве­стиций и ее доли в общем капитале инвестора. Например, 5 % капитала можно вложить в акции с высокой степенью риска, но сулящие большие доходы. В то же время неразумно было бы вкладывать в эти акции, 25 и более процентов капитала.

Для наших дальнейших рассуждений необходимо ввести очень важ­ное понятие – принцип рыночного равновесия.

Данный принцип основан на том, что рынок ценных бумаг являет­ся хорошо сбалансированной системой. Это означает, что при нормаль­ном состоянии рынка продавцы ценных бумаг и их покупатели постоян­но и активно взаимодействуют и, как следствие, разрыв между ценами спроса и предложения очень незначителен, операторы фондового рынка быстро приходят к признанию их равновесных значений. Обеспечивается подобное положение тем, что все обращаемые на рынке ценные бумаги имеются в любое время в продаже и, кроме того, адми­нистрацией фондовых бирж предусмотрен ряд административных мер, направленных на уменьшение разрыва в ценах спроса и предложения.

На основе принципа рыночного равновесия можно сделать вывод: доходности `r_m соответствует минимально возможная степень риска G_m , или максимально возможная прибыль, отвечающая риску G_m, достигается при структуре портфеля, идентичной структуре рыночного оборота.

В силу этого главной задачей инвестора становится максималь­ное воспроизведение в своем портфеле структуры рынка с периодичес­кой ее корректировкой.

Важнейшим элементом фондового рынка являются гарантированные ценные бумаги с фиксированным доходом, например, государственные облигации. Отсутствие риска по этим бумагам влечет за собой и мини­мальный уровень доходности. В силу этого гарантированные бумаги являются главным регулятором прибылей и рисков.

Предположим, что значение доходности по гарантированным сум­мам является величина Z. В этом случав любой инвестиционный порт­фель, имеющий бумаги с той или иной степенью риска, даст более вы­сокую прибыль, чем аналогичные по объему инвестиции в гарантирован­ные бумаги. Следовательно, можно заключить, что замена любых цен­ных бумаг на более прибыльные повышает риск портфеля.

Из сказанного вытекает соотношение, известное под названием линия капитала, связывающего показатели эффективности и степень рис­ка портфеля, т.е.

r_p и G_p (r_pr_m; G_p G_m)

где r_p - доходность (эффективность) портфеля акций;

Z - гарантированный процент, выплачиваемый по государствен­ным ценным бумагам;

r_m - средняя рыночная доходность акций за период К;

G_m - среднеквадратическое отклонение рыночных ценных бумаг;

G_p - среднеквадратическое отклонение акций портфеля ценных бумаг.

При r_р = r_m и G_p= G_m выражение (2.9) принимает вид:

(2.10)

Для дальнейшего анализа структуры портфеля используем едва ли не самый главный показатель рынка ценных бумаг - бета-коэффициент (b ), рассчитываемый по формуле

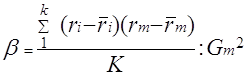(2.11)

Значения символов, входящих в данное выражение, приведены в (5.1) - (5.10).

Коэффициент бета оценивает изменения в доходности отдельных акций в сопоставлении с динамикой рыночного дохода. Ценные бумаги, имеющие бета выше единицы, характеризуются как агрессивные и яв­ляются более рискованными, чем рынок в целом. Ценные бумаги с бета меньше единицы характеризуются как защищенные и остаются менее рис­кованными, чем рынок в целом. Кроме того, коэффициент бета может быть положительным или отрицательным. Если коэффициент бета — ве­личина положительная, то эффективность ценных бумаг, для которых рассчитан b , будет аналогична динамике рыночной эффективности. При отрицательном бета-коэффициенте эффективность данной ценной бу­маги будет снижаться при возрастании эффективности рынка.

Например, доход на конкретные акции вырос на 10 %, и уровень дохода на рынке банка повысился на 10 %, или же наоборот, снижение рыночного дохода сопровождалось таким падением дохода на данные ак­ции, означающим, что доходность данных акций и рынка изменяется одинаково. Бета для данных акций равна I. Если же доход на акции вырос на 12 %, в то время как на рынке он увеличился на 10 %, то из­менение в доходе на акции в 1,2 раза превысит изменение рыночного дохода; соответственно бета для данных акций составит 1,2. Если доходность акций увеличилась на 8 % при росте рыночного дохода на 10 %, то изменение дохода на акции составит лишь 0,8 от изменения рыночного дохода; отсюда, бета для акции будет равна 0,8. Бета-коэффициент также используется для определения ожидаемой ставки до­хода. Модель оценки акций предполагает, что ожидаемая ставка дохода на конкретную ценную бумагу равна безрисковому доходу ( Z) плюс коэффициент-бета (показатель риска), помноженный на базовую премию за риск (`r<sub>m</sub>- Z). В качестве показателя `r_m обычно берется вели­чина, рассчитанная по какому-либо широко известному рыночному ин­дексу (в России используется индекс АК & M акций промышленных фирм). Данная модель описывается следующей формулой:

(2.12)

где `r_i - ожидаемый (средний) доход на конкретную ценную бумагу;

Z- ставка дохода на безрисковую ценную бумагу;

b_i - бета-коэффициент;

`r_m - средняя рыночная ставка дохода;

(`r_m-Z)- рыночная премия за риок.

формула (2.12) получена после ряда преобразований формул (2.9)

и (2.10).

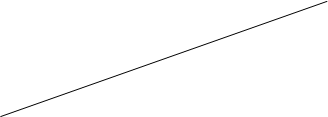
Линейная связь, описанная формулой (2.12), показана на рис. 2.1 и называется линия рынка ценных бумаг.

r_i

Рыночная премия за риск

r_m

Z

1.0 b_i

Рис. 2.1. Линия рынка ценных бумаг

Для того чтобы доход на ценную бумагу соответствовал риску, цена на обыкновенные акции должна снижаться, за счет этого будет ра­сти ставка дохода до тех пор, пока она не станет достаточной для компенсации риска, принимаемого инвестором. На равновесном рынка на все обыкновенные акции устанавливаются цены на таком уровне, при ко­тором ставка доходов на каждую акцию уравновешивает инвестору риск, связанный с владением данной бумагой. В этом случае, в соответствии с уровнями риска и ставки дохода, все акции размещаются на прямой рынка ценных бумаг.

Ранее мы концептуально определили риск как степень определен­ности или неопределенности, связанной с получением ожидаемых в бу­дущей доходов. Теория рынка каптала выделяет два вида риска: систематический риск и несистематический риск. Систематический риск характеризует неопределенность получения будущих доходов, обуслов­ленную вариацией среднесрочного дохода.

Несистематический риск обусловлен особенностями соответству­ющей отрасли, конкретной фирмы, типом инвестиционного участия.

Таким образом, совокупный риск определяется данными система­тическими и несистематическими факторами.

Исходя из этого положения, риск отдельной акции можно выразить формулой:  (2.13)

где G_i - характеристика риска i-того вида акций;

 характеризует влияние общего состояния рынка на кон­кретные ценные бумаги;

G_Ei² - характеризует вариацию несистематического риска, т.е. риска, не связанного с положением на рынке.

В выражении (2.11) используются средние величины r_i, и r_m Из теории статистики известно, что при расчете средних величин проис­ходит элиминирование случайных факторов, воздействующих на осредняемый признак. Следовательно, в формуле (2.11) устранено влияние не­систематического риска. Поэтому для более точного вычисления доход­ности i-той акции и портфеля в целом целесообразно использовать вы­ражение, подученное в результате преобразования (2.12). Ниже приво­дится это выражение

(2.14)

где E_i- величина несистематического риска.

Доходность же портфеля определяется аналогично

  (2.15)

Подстрочный символ р обозначает показатели, относящиеся к портфели ценных бумаг.

При этом и определяются как

где x_ip - удельное содержание в портфеле i-x ценных бумаг.

Вместе с выражением (2.14) и (2.15) выполняются следующие ра­венства:

(2.16)

(2.17)

Анализ выражений (2.16) к (2.I7) позволяет сделать вывод, что диверсификация портфеля снижает уровень риска. Действительно, если в портфеле находятся акции одного вида на сумму 20 млн.руб., то за­мена их на два вида по 10,0 млн.руб., но с теми же значениями b-коэффициента, сохраняет прибыль r_p, но понижает риск G_p.

Формулы (2.14) и (2.15) являются главными расчетными. Инвестор или исследователь, используя публикуемую статистику по r_i и r_m за прошедший период К , всегда может определить b_i и b_p по формулам:

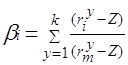(2.18)

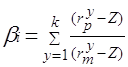(2.19)

где - доходность i-той акции в y -том периоде;

 - доходность рыночная в y-том периоде;

- доходность портфеля в y -том периоде;

Z - доходность безрисковых бумаг.

При рассмотрении вопроса об оптимизации структуры портфеля не­обходимо остановиться еже на одном показателе -  (альфа).

Известно, что курс акции подвержен частым колебаниям, которые не всегда адекватны реальным изменениям в делах компании-эмитента. Поэтому многие операторы фондового рынка пытаются вовремя восполь­зоваться такими непродолжительными ситуациями для извлечения прибы­ли. Наряду c этим на рынке всегда есть бумаги с устойчиво завышен­ными или заниженными ценами, причем эти отклонения от "истинной" цены носит долговременный характер. Мерой этого отклонения служит показатель . который рассчитывается как

2.20

При a_i < 0 действовавшая цена считается завышенной, а при > 0-заниженной.

На основе a-анализа инвесторы уточняют состав портфеля, выби­рая при прочих равных условиях те акции, которые имеют положитель­ные a.

Пример 3.1. На основе опубликованных данных о доходности ак­ций компании "Прометей" и рыночного индекса доходности акций за пе­риод с 01.01.95. по 01.01.97 (24 месяца) выбраны следующие данные (графы 1-3 из таблицы 2.1).

Определим b-коэффициент акций компании "Прометей", если доход по безрисковым бумагам составляет 5,0 % (Z = 0,03).

Таблица 2.1.

№ акции	Доход на акцию компании «Прометей»,ri	Рыноч.показатель дохо-ти акций, rm	ri  -` ri	rm  - `rm	(ri  - ri)* (rm  - rm)	(rm  - rm)2	ri  - Z	rm - Z
1	0,033	0,06	0,0188	0,0531	0,0010	0,0028	0.0030	0.030
2	0,034	0,046	0,0198	0,0391	0,0008	0,0015	0.0040	0.016
3	0,030	0,048	0,0158	0,0411	0,0006	0,0017	0.000	0.018
…
…
…
23	0,08	0,028	0,0658	0,0211	0,00014	0.0004	0.050	-0.0020
24	0,023	0,033	0,0088	0,0261	0,0002	0.0007	-0.0070	0.0030
Сумма	0,34	0,166			0,040	0.04450	0.694	0.770

1.  ;

2. 

3. 

4. 

5.  по (2.11)

6.  по (2.18)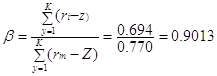

Рассчитанные значения коэффициента - ß свидетельствуют, что акции компании "Прометей" являются менее рискованными, чем рынок в целом. Кроме того, учитывая, что полученные коэффициенты положитель­ны, динамика эффективности акций "Прометей" будет соответствовать динамике рыночной эффективности ценных бумаг.

Пример 2.2. На основе данных предыдущего примера определить показатель α - (альфа) акций компании "Прометей" по состоянию на 01.01.97. no (2.20)

Так α > 0, то цена акций несколько занижена.

2.4. Основные характеристики облигаций и методы расчета их доходности.

Облигации относится к ценным бумагам с фиксированным доходом. Они могут выпускаться государством, региональными властями, финансо­выми институтами, а также различными корпорациями.

Облигация - ценная бумага, удостоверяющая отношение займа меж­ду кредитором - владельцем облигации и должником - эмитентом облига­ции. Облигация удостоверяет внесение ее владельцем денежных средств и подтверждает обязательство возместить ему номинальную стоимость облигации в заранее установленный срок с уплатой фиксированного про­цента.

К основным параметрам облигации относятся: номинальная цена, выкупная цена s случае, если она отличается от номинальной, норма доходности и сроки выплаты процентов. Момент выплаты процентов ого­варивается в условиях эмиссии и пожег производиться раз в год, по полугодиям или поквартально.

В мировой практике используется несколько способов выплаты до­ходов по облигациям, в их числе: установление фиксированного про­центного платежа, применение ступенчатой процентной ставки, исполь­зование плавающей ставки процентного дохода, индексирование номи­нальной стоимости облигации, реализация облигаций со скидкой (ди­сконтом) против их нарицательной цены, проведение выигрышных займов.

Установление фиксированного процентного платежа является распространенной и наиболее простой формой выплаты дохода по облигаци­ям.

При использовании ступенчатой процентной ставки останавливают­ся несколько дат, по истечении которых владельцы облигаций могут либо их погасить, либо оставить до наступления следующей даты. В каждый последующий период ставка процентов возрастает.

Ставка процента по облигациям может быть плавающей, т.е. изме­няющейся регулярно (каждые полгода и т.п.) в соответствии с динами­кой ставки рефинансирования Центрального Банка или уровнем доходно­сти государственных ценных бумаг, размещаемых путем аукционной про­дажи.

В отдельных странах в качестве антиинфляционной меры практику­ет выпуск облигаций с номиналом, индексируемым с учетом роста индек­са потребительских цен.

По некоторым облигациям проценты не выплачиваются. Их владель­цы получают доход благодаря тому, что покупают эти облигации с ди­сконтом (скидкой против нарицательной стоимости), а погашают - по номиналу.

 Доход по облигациям может выплачиваться в форме выигрышей, получаемых отдельными их владельцами по итогам регулярно проводимых тиражей.

Облигации, являясь объектом купли-продажи на рынке ценных бумаг, имеют рыночную цену, которая в момент эмиссии может быть равна номиналу, а также быть ниже или выше его. Рыночные цены существенно различаются между собой, поэтому для достижения их сопоставимости рассчитывается курс облигации. Под курсом облигации понимают покупную цену одной облигации в расчете на 100 денежных единиц номинала. Курс облигации зависит от средней величины ссудного процента на рын­ке капиталов, существующего в данный момент, срока погашения, степе­ни надежности эмитента и ряда других факторов.

Расчет курса производится по формуле:

(2.21)

где Р_к - курс облигации;

Р - рыночная цена;

N - номинальная цена облигации.

Доходность облигаций характеризуется рядом параметров, которые зависят от условий, предложенных эмитентом. Так например, для облигаций, погашенных в конце срока, на которые они выпущены, доходность измеряется купонной доходностью, текущей доходностью и полной доход­ностью.

Купонная доходность - норма процента, которая указана на цен­ной бумаге и которую эмитент обязуется уплатить по каждому купону. Платежи по купонам могут производиться раз в квартал, по полугоди­ям или раз в год.

Например, на облигации указана купонная доходность в 11,75 % годовых. Номинал облигации 100 тыс. руб. На каждый год имеется два купона. Это значит, что облигация принесет полугодовую прибыль 5,875 тыс. руб. (100 *0.1175 * 0,50), а за год 11.75 тыс. руб.

Текущая доходность характеризует выплачиваемый годовой процент на вложенный капитал, т.е. на сумму, уплаченную в момент приобрете­ния облигации. Текущая доходность определяется по формуле:

(2.22)

 где  норма доходности по купонам;

N - номинальная цена облигации;

Р - рыночная цена (цена приобретения).

Например, если купонная доходность =11,75 %, а курс облига­ции 95,0, то текущая доходность составит

Вместе с тем текущая доходность не учитывает изменения цены об­лигации за время ее хранения, т.е. другого источника дохода.

Полная доходность учитывает все источники дохода. Показатель полной доходности измеряют процентной ставкой, называемой ставкой помещения. Начисление процентов по ставке помещения на цену приобре­тения дает доход, эквивалентный фактически получаемому по ней дохо­ду за вес! период обращения этой облигации до момента ее погашения. Ставка помещения является расчетной величиной и в явном виде на рын­ке ценных бумаг не выступает.

Стоимость облигации равна сумме двух слагаемых - современной стоимости ее аннуитетов (приведенной сумме ежегодных выплат процент­ных платежей) и современной стоимости ее номинала:

P = N g a_n/i + N (1+i)^-n = N (ga_n/i + (1+i)^-n) (2.23)

Если использовать 2.1, то

P = (ga_n/i + (1+i)^-n) * 100

где Р - рыночная цена облигации;

Рк – курс облигации;

N - номинал облигации;

g- купонная ставка;

n- время от момента приобретения до момента погашения обли­гации;

i - ссудный процент, предлагаемый банками в момент продажи облигации.

Пример 2.3. По облигации номинальной стоимостью в 100 тыс.руб. в течение 10 лет (срок до ее погашения) будут выплачиваться ежегод­но в конце года процентные платежи в сумме 10 тыс.руб. ( = 10 %), которые могут быть помещены в банк под 11 % годовых.

Рыночная цена облигации по (2.25) составит:

В данном случае облигация продается с дисконтом (ниже номинала), т.к. = 10 % <i = 11 %, Р_к = 100.

Предположим далее, что ставка банковского процента снизилась с 11 % до 9,5 %. Номинальная стоимость облигации и размер ежегодных выплат при этом сохраняется неизменным. Тогда рыночная цена облига­ции составит:

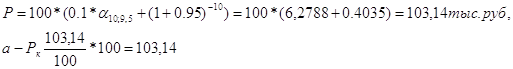
В этом случае облигация продается с премией, т.к. . = 10 % > i' = 9,5 %, a P>100.

Так как цена облигации при ее продаже эквивалентна будущим по­ступлениям от нее, то при приближении момента ее выкупа курс обли­гации, купленной с премией, понижается. Обусловлено это тем, что по всей уже выплачена большая часть доходов и к моменту выкупа остается получить только ее номинальную стоимость. Курс же облигации, куплен­ной с дисконтом, будет повышаться, так как в момент ее погашения владелец получит сумму, равную номиналу (приобрел же он ее по пониженной цене).

Таким образом, с приближением даты выкупа происходит погашение дисконта. Погашенный дисконт увеличивает оценку облигации и ее курс.

Для получения показателя, дающего количественную характеристику зависимости цены облигации от купонного дохода и рыночной процент­ной ставки,обозначим:

N(1 + i)^-n= Q - современная стоимость номинала облигации.

Разность между продажной и выкупной ценой облигации (номина­лом облигации) равна

Е = Р -N

Сделав ряд преобразований, определим эту разность, как

E = g-i/i *Na_n/i  (2.25)

При g=i, Е=0, т.е. облигация продается по номиналу.

При g>i, Е - величина положительная и облигация продает­ся с премией.

При g<i, Е < 0 и облигация продается с дисконтом.

Ранее мы рассматривали понятие - ставка помещения. Естественно, что любой инвестор, планирующий сделать инвести­ции в облигации, должен рассчитать ставку помещения.

Для приближенной оценки ставки помещения соотносят годовой до­ход от облигации со средней ее ценой. Средняя цена определяется на основе номинала и цены покупки. Для облигаций, приобретенных с дис­контом, ставка помещения равна:

 I = (gN + (N-P)/n): (P+N)/2 (2.26)

а для облигаций, купленных с премией:

I = (gN + (N-P)/n): (P+N)/2 (2.27)

где n - числи лет, оставшихся до погашения;

g - годовой купонный доход;

P- цена приобретения;

N - номинал облигаций.

По данным примера 5.5 рассчитаем ставку помещения для случая продажи облигации с дисконтом:

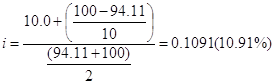
Приведем ряд расчетных формул показателей доходности для дру­гих видов облигаций.

Облигации без выплаты процентов. Для данного вида облигаций доходом является разность между ценой погашения (номиналом) и ценой приобретения. В этом случае показатель доходности равен

(2.28)

 где P_k - курс облигации, Р„ ^ 100;

n - срок от момента приобретения до момента выкупа.

Облигации с выплатой процентов в конце срока обращения. Владе­лец данного вида облигаций в конце срока обращения получит ее номи­нальную стоимость с начисленными процентами. Показатель доходности:

I = (100 : P_k)^1/n (1+g) – 1 (2.29)

где g - проценты, начисляемые на номинал.

Пример 2.4. Банк выпустил облигации со сроком погашения через 10 лет. Начисление процентов на номинал – 6 % годовых. Выплата про­центов и номинальная стоимость выплачивается при погашении. Опреде­лить доходность облигации (ставку помещения), если ее курс при пер­воначальной реализации составил: а) 108,0; б) 92,0:

а) 5.19 %

б)6,89 %

2.5. Дополнительные характеристики облигаций.

Доходность является важнейшим, но не единственным критерием выбора облигаций. Другим показателем привлекательности для инвесто­ра того или иного вида облигации является продолжительность срока до ее погашения. При увеличении последнего растет степень финансового риска для ее владельца. Безусловно, риск приобретения облигаций с купонными доходами значительно ниже риска, связанного с облигаци­ями, выплата процентов, по которым производится в конце срока. В свя­зи с этим существует ряд показателей, которые характеризуют в той или иной степени особенности распределения доходов в период времени от момента покупки облигации до момента погашения.

Одним из таких показателей является средний срок облигации. При ежегодных купонных выплатах средний срок выплат определяется как:

Т = h * (g (1+h):2 + 1) : gh + 1 (2.30)

где h - сроки платежей по купонам в годах;

g - купонный процент.

Пример 2.5.Облигация номиналом 10000 руб. выпущена со сроком погашения через 4 года. Ежегодно по купонам выплачивается 12 % от номинала. Определить средний срок облигации

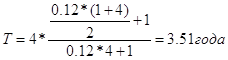
Наряда с показателей среднего срока облигации существует близ­кий ему по экономическому смыслу показатель, характеризующий сред­нюю продолжительность платежей. Иногда его называют показателем из­менчивости; обозначим его символом.

Данный показатель является средней величиной.

В случае, когда проценты по облигациям выплачиваются ежегодно, расчет средней продолжительности платежей производится по формуле;

D = S t_{j *}S_j V^t : S S_j V (2.31)

Пример 2.6. Облигация выпущена сроком на 4 года, номиналом 1000 руб. Ежегодно выплачиваются по купонам 12 % годовых, рыночная процентная ставка - 12,5 %. Рыночная цена облигации 985 руб.

Определить показатель продолжительности платежей.

Рассчитаем все элементы, входящие в (2.31)

t	Vt	Sj	SjVt	t SjVt
1	0.8889	120	106.668	106.668
2	0.7901	120	94.815	189.630
3	0.7023	120	84.280	252.840
4	0.6243	120+1000	692.973	3345.980

D = 3345,980 : 985,0 = 3,4 года.

Приведенные формулы для расчета величин Т и Д показывают, что величина Т не зависит от рыночной процентной ставки (ссудного про­цента), в то же время величина Д зависит от ее изменения: с ростом ссудного процента его влияние на отдаленные по времени платежи пада­ет, что, в свою очередь, снижает величину Д.

Поэтому основным назначением показателя Д является определение эластичности цены по процентной ставке, т.е. измерение степени колеблемости цены облигации при незначительных изменениях величины процентной ставки на денежном рынке.

Решение этой задачи осуществляется с помощью модифицированной величины Д, которая в отечественных экономических публикациях по­лучила название модифицированной изменчивости (МД).

 МД = Д/ (1+i:p) (2.32)

Где Д - средняя продолжительность платежей;

i - рыночная процентная ставка;

Р - число выплат процентов в году.

Изменение цены облигации в результате изменения процентной ставки определяется по формуле:

▲P = - 0.01*МД * ▲ i * P (2.33)

где ▲P - изменение цены облигации;

▲ i - изменение рыночной процентной ставки.

Пример 2.7. По данным примера 2.4 рассчитаем показатель моди­фицированной изменчивости

Определим, как изменится цена облигации, если рыночная процент­ная ставка возрастет с 12,5 % до 12,8 %.

▲Р= -0001*3,0222*0,3*985=-8,9306.

Откуда ожидаемое значение цены составит:

985,0 - 8,9306 = 976,0694.

Реакция цены облигации на значительные изменения рыночной про­центной ставки измеряется с помощью показателя, получившего назва­ние выпуклость (С_x).

Расчет производится по формуле

С_х= 1/(1+ i:p) * (M² +Д² + Д: Р) (2.34)

Где М² - дисперсия показателей времени платежа;

значения остальных символов те же, что и в (2.11-2.12).

 М² = 1/Р S t² S_j V^t – Д² (2.35)

где Р - цена облигации.

Сдвиг в цене облигации в результате значительного изменения рыночных процентных ставок определяется как

▲P = - РМД * ▲ i: 100 +( (0.5P * C_x▲ i) : 10000) (2.36)

Пример 2.8. Рассмотрим возможность изменения цены облигации, если рыночная процентная ставка возросла с 12,5 % до 15,0 %, осталь­ные условия аналогичны примерам 2.4 и 2.5.

t	t2	Vt	Sj	t2 SjVt
1	1	0.8889	120	106.668
2	4	0.7901	120	189.630
3	9	0.7023	120	252.840
4	16	0.6243	120+1000	11187.360
Итого				12431,808

М² = 1,0611

Рассчитаем С_х:

Так как ▲i = 15- 12,5 = 2,5 %, то по (2.15) находим

▲Р= - 985,0 * 3,0222 * (15 - 12,5 / 100) + (0,5 * 985,0 * 14,2410 * 2,5²) / 1000= - 70,038

т.е. рост процентной ставки на 2,5 % вызывает снижение цены облигации до уровня 985,0 + (-70,038) = 914,962 руб.