Навигация
Этап. За первые два года получения дохода их современная величина составит
3 этап. За первые два года получения дохода их современная величина составит
![]()
т.е. эта величина меньше суммы инвестиций с начисленными процентами 342,97 < 470. За три года современная величина дохода будет равна
![]()
т.е. больше, чем стоимость инвестиций.
Отсюда, срок окупаемости (при условии, что доход может выплачиваться и за часть года) составит
nок = 2+ ((470+342.97) : 225,4) = 2,56 года.
Величина 225,4 получена как 3500 • 1,1-3.
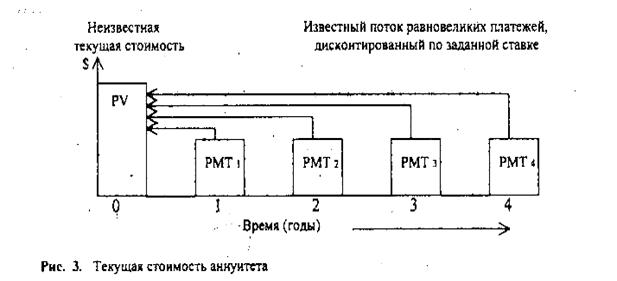
Рассмотрим определение срока окупаемости для доходов, которые можно представить в виде некоторых упорядоченных последовательностей (аннуитетов). Начнем с самого простого случая: с равномерного дискретного (один раз в конце года) поступления доходов. Из условий полной окупаемости за срок nок при заданной ставке –i следует равенство суммы капитальных вложений современной стоимости аннуитета.
![]() , осюда
, осюда
|
| (3.6) |
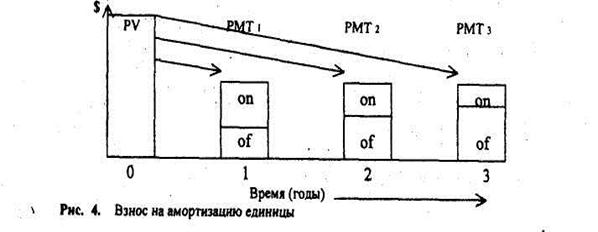
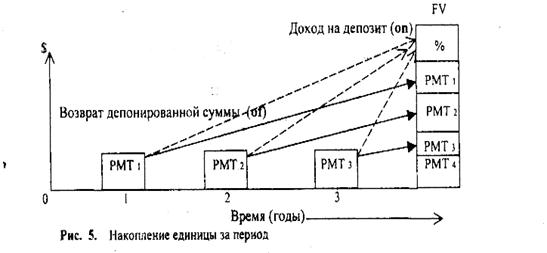
Аналогичным путем можно найти срок окупаемости для других видов распределения отдачи. В каждом таком случае капиталовложении приравниваются к современной величине финансовых рент, т.е. IC = А, а члены денежного потока Pk = R - члену ренты, число членов потока в году - Р.
Пример 3.9. Инвестиции к началу поступления доходов составили 6 млн.у.д.е., годовой доход ожидается на уровне 1,05 млн.у.д.е., поступлении ежемесячные при принятой ставке сравнения i = 10 %.
Исходя из формулы для расчета срока постоянных рент, постнумерандо
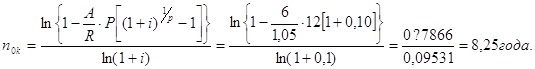
Для сравнения заметим, что без учета фактора времени получения доходов срок окупаемости составит ny= 5,71 года (6: 1,05=5,71)
Как видим, разница существенная.
Не всякий уровень дохода при прочих равных условиях приводит к окупаемости инвестиций. Срок окупаемости существует, если не нарушаются определенные соотношения между поступлениями и размером инвестиций. Так, при ежегодном поступлении постоянных доходов (один раз в году) это соотношение имеет вид: Рк> IC * i , при поступлении постоянных доходов несколько раз в году (Р-раз в году): Рк>P (1+i)1/p * IC , при непрерывном поступлении доходов: Рк> ln(1+i)* IC.
Если перечисленные требования не выполняются, то капиталовложения не окупаются за лисой срок, точнее, этот срок равен бесконечности.
Приведенные неравенства, вероятно, окажутся полезными для быстрой оценки ситуации.
Пример 3.10 С = 10 %. Капвложения - 6 млн.у.д.е. Ожидаемая годовая отдача от инвестиций 0,5 млн.у.д.е. исходя из приведенного неравенства, отдача должна быть больше, чем IC • i = 0,1 * 6,0 = 0,6, но 0,6 < 0,5. Таким образом, при заданной уровне отдачи инвестиции не окупаются. В то же время упрощенный срок окупаемости (без учета фактора времени) говорит о том, что инвестиции окупятся через 12 лет
![]()
Основной недостаток показателя срока окупаемости nok как меры эффективности заключается в том, что он не учитывает весь период функционирования инвестиций и, следовательно, на него не влияет вся та отдача, которая лежит за пределами nok. Поэтому показатель срока окупаемости не должен служить критерием выбора, а может использоваться лишь в виде ограничения при принятии решения, т.е., если срок окупаемости проекта больше, чем принятое ограничение, то он исключается из списка возможных инвестиционных проектов.
3.4. Определение внутренней нормы доходности инвестиционных проектов.Внутренняя норма доходности, прибыли (internal rats of return, IRR) является показателем, широко используемым при анализе эффективности инвестиционных проектов.
Реализация любого инвестиционного проекта требует привлечения финансовых ресурсов, за которые всегда необходимо платить. Так, за заемные средства платятся проценты, за привлеченный акционерный капитал - дивиденды и т.д.
Показатель, характеризующий относительный уровень этих расходов, является "ценой" за использованный (авансируемый) капитал (СС). При финансировании проекта из различных источников этот показатель определяется по формуле средней арифметической взвешенной.
Чтобы обеспечить доход от инвестированных средств или, по крайней мере, их окупаемость, необходимо добиться такого положения, когда чистая текущая стоимость будет больше нуля или равна ему. Для этого необходимо подобрать такую процентную ставку для дисконтировании членов потока платежей, которая ооеспечит получение выражений NPV^> 0 или NPV = 0.
Как оказывалось ранее в (3.2), такая ставка (барьерный коэффициент) должна отражать ожидаемый усредненный уровень ссудного процента на финансовом рынке с учетом фактора риска.
Поэтому под внутренней нормой доходности понимают ставку дисконтирования, использование которой обеспечивает равенство текущей стоимости ожидаемых денежных оттоков и текущей стоимости ожидаемых денежных притоков, т.е. при начислении на сумму инвестиций процентов по ставке, равной внутренней норме доходности, обеспечивается получение распределенного во времени дохода.
Показатель внутренней нормы доходности - IRR характеризует максимально допустимый относительный уровень расходов, которые могут быть произведены при реализации данного проекта.
Например, если для реализации проекта получена банковская ссуда, то значение IRR показывает верхнюю границу допустимого уровня банковской процентной ставки, превышение которой делает проект убыточным.
Таким образом, смысл этого показателя заключается в том, что инвестор должен сравнить полученное для инвестиционного проекта значение IRR. и "ценой" привлечиньых финансовых ресурсов (cost of capital - CC)
Если 1RR. > СС, то проект следует принять;
1RR < СС, проект следует отвергнуть;
IRR = CС, проект ни прибыльный, ни убыточный. Практическое применений данного метода сводится к последовательной итерации, с помощью которой находится дисконтирующий множитель, обеспечивающий равенство NPV=0
Рассчитываются два значения коэффициента V1 < V2 таким образом, чтобы в интервале (V1,V2) функция NPV=. f (V) меняла свое значение с " + " на " - " или наоборот. Далее используют формулу:
IRR = i1 + (NPV (i1) : (NPV (i1) - NPV (i2)) (3.7)
где i1 - значение процентной ставки в дисконтном множителе, при которой f (i1) > 0, f (i1) < 0
i2 - значение процентной ставки в дисконтном множителе, при котором (f (i2) > 0), (f (i2) < 0).
Точность вычислений обратна длине интервала (i1, i2 ). Поэтому наилучшая апроксимация достигается в случае, когда длина интервала принимается минимальной (1%).
Пример 3.11.Требуется определить значение IRR (процентную ставку) для проекта, рассчитанного на три года, требующего инвестиций в размере 20,0 млн.у.д.е. и имеющего предполагаемые денежные поступления в размере Р1 = 0,0 млн. (1-й год); Р2 = 8,0 млн. (2-й год) и Р3 = 14,0 млн. (3-й год).
Возьмем два произвольных значения процентной ставки для коэффициента дисконтирования: i1= 15 % и i2 = 20 %. Соответствующие расчеты приведены в таблицах.
Таблица 3.4.
| Год t | Поток | Расчет 1 | Расчет 2 | ||
| i1= 15 %
|
| i1= 20 %
|
| ||
| 0-й 1-й 2-й 3-й | -20 6,0 8,0 14,0 | 1,0 0,8696 0.7561 0.6575 | -20.0 5.2176 6,0488 9,2050 | 1.0 0.8333 0,6944 0,5787 | -20,0 4,9998 5.5552 8,1018 |
| 0,4714 | -1,3452 | ||||
По данным расчета 1 и 2 вычислим значение IRR
1) ![]()
Уточним величину ставки, для чего примем значения процентных ставок, равное i1 = 16 %, i2 = 17 % и произведем новый расчет.
Таблица 3.4.
| Год t | Поток | Расчет 1 | Расчет 2 | ||
| i1= 16 %
|
| i1= 20 %
|
| ||
| 0-й 1-й 2-й 3-й | -20 6,0 8,0 14,0 | 1,0 0,8662 0.7432 0.6407 | -20.0 5.1972 5,9200 8.9698 | 1.0 0.8547 0,7305 0,6244 | -20,0 5.1282 5.8440 8,7416 |
| 0,0870 | -0.2862 | ||||
По данным расчета 1 и 2 вычислим значение IRR
2) ![]()
I RK. = 16,25 % является верхним пределом процентной ставки, по которой уирма помет окупить кредит для финансирования инвестиционного проекта. Для получения прибыли фирма должна брать кредит по ставки менее 16,25 %.
3.5. Расчет индексов рентабельности и коэффициента эффективности инвестиций.
Индекс расчета (profitability index - PI) метод расчета данного показателя является как бы продолжением метода расчета чистого приведенного дохода – NPV. Показатель PI в отличие от показателя NPV является относительной величиной.
Если инвестиции осуществлены разовым вложениям, то данный показатель рассчитывается по формуле:
PI = S Pk : (1+i)n IC = S PkVn : (1+i)n
где Рк - чисты и доход;
1C - стартовые инвестиции;
Vn- дисконтный множитель.
где IC - размеры инвестиционных затрат в периоды t = 1, 2, ... n.
Пример 3.12. Показатели современных величин вложений (![]() ) равны.5,1568 млн.у.д.е., а современная величина частых доходов
) равны.5,1568 млн.у.д.е., а современная величина частых доходов
![]()
равна 5,4452 млн. у. д. е.
При этих условиях индекс рентабельности будет равен
![]()
Если показатель РI = I, то это означает, что доходность инвестиций точно соответствует нормативу рентабельности (ставке сравнения). При РI < 1
Расчет коэффициента эффективности инвестиций (ARR)
Суть метода заключается в том, что делится величина среднегодовой прибыли (РN) на среднюю величину инвестиции. Сам коэффициент выражается в процентах. Средняя величина инвестиции находится делением исходной суммы капитальных вложении на два, если предполагается, что по истечении срока реализации анализируемого проекта все капитальные затраты будут списаны, если же допускается наличие остаточной или ликвидационной стоимости (RV), то ее величина долина быть исключена.
Таким образом, величина этого коэффициента рассчитывается как
![]()
Данный показатель можно сравнивать с коэффициентом рентабельности.
Основной недостаток данного метода заключается в том, что он не учитывает временного фактора при формировании денежных потоков.
3.6.Анализ альтернативных инвестиционных проектов.
Оценка инвестиций в условиях дефицита финансовых ресурсов.
Одним из побудительных мотивов, заставляющих фирму выбирать из нескольких перспективных и выгодных инвестиционных проектов один или несколько - это ограниченность финансовых средств. Лимитирование финансовых средств для инвестиций есть фиксированный предел годового объема капитальных вложений, который может себе позволить фирма, исходя из своего финансового положения. При наличии финансовых ограничений на инвестиции фирма монет принять некоторые инвестиционные проекты, составляющие такую комбинацию, которая обеспечит наибольший эффект.
Предположим, что у фирмы есть следующие предложения для инвестирования средств, проранжированные в убывающем порядке по индексу рентабельности (отношение текущей стоимости будущих чистых
денежных потоков к первоначальным затратам):
Таблица 3.6.
| Инвестиционные предложения | 3 | 7 | 4 | 2 | 6 | 1 |
| Индекс рентабельности | 1,22 | 1,2 | 1,19 | 1,13 | 1,08 | 1,04 |
| Первоначальные (стартовые) затраты, у.д.е. | 800000 | 200000 | 350000 | 250000 | 400000 | 20000 |
Исходя из своего финансового положения, фирма планирует ассигновать в инвестиции 2,0 млн. у.д.е. В этом случае фирма выберет из предложенных проектов те из них, которые обещают наибольшую рентабельность, а сумма всех первоначальных затрат не превысит 2,0 млн.у.д.е.
В нашем случае это предложение (3,7,4,2 и 6), т.к. они обладают наиболшей рентабельностью, а сумма стартовых капиталов равна 2,0 млн. у.д.е. (800000 + 20000 + 350000 + 250000 + 400000).
Фирма не станет принимать предложение № I, хотя первоначальные затраты значительно уступают другим проектам, а его рентабельность превышает единицу, что в других условиях было бы вполне приемлемым.
При рассмотрении нескольких альтернативных инвестиционных проектов в зависимости от выбранного метода его экономической оценки можно получить далеко не однозначные результаты, зачастую противоречащие друг другу. Вместе с тем, между рассмотренными показателями эффективности инвестиций (NPV, PI, IRR) существует определенная взаимосвязь.
Так, если NPV > 0, то одновременно 1RR, > GC и PI > I;
при NPV = 0 одновременно IRR= СС и PI = I.
Для решения вопроса о том, каким критерием в таком случае лучше воспользоваться, рассмотрим пример.
Пример 3.13. Фирма рассматривает четыре варианта инвестиционных проектов, требующих равных стартовых капиталовложений (2400 тыс.у.д.е.). Необходимо произвести экономическую оценку каждого к выбрать оптимальный. Финансирование проектов осуществляется за счет банковской ссуды в размере 18 % годовых.
Динамика денежных потоков и рассчитанные показатели эффективности приведены в таблице 3.7.
Таблица 3.7.
| Год | Прогнозируемые денежные потоки, тыс. у.д.е. цые денедные г ютоки^ ты с.у. ii ^„——— | ||||
| Проект I | Проект 2 | Проект 3 | Проект 4 | ||
| 0-й | -2400 | -2400 | -2400 | -2400 | |
| 1-й | 0 | 200 | 600 | 600 | |
| 2-й | 200 | 600 | 900 | 1800 | |
| 3-й | 500 | 1000 | 1000 | 1000 | |
| 4-й | 2400 | 1200 | 1200 | 500 | |
| 5-й | 2500 | 1800 | 1500 | 400 | |
| Показатели | |||||
| NPV | 809,6 | 556,4 | 307,2 | 689,0 | |
| PI | 1,337 | 1,231 | 1,128 | 1,29 | |
| 1^ | 22,31 % | 20,9 % | 27,7 % | 27.8 % | |
| PP | 2,33 года | 2,0 года | 2,16 года | 1,79 года | |
Анализ данных, приведенных в таблице, позволяет сделать следующие выводы:
1) наилучший показатель NPV= 809,6 тыс.у.д.е. принадлежит проекту № 1. Следовательно, принятие данного проекта обещает наибольший прирост капитала:
2) в этом же "первом" инвестиционном проекте наибольшее значение из всех рассматриваемых имеет показатель PI = 1,337, т.е. приведенная сумма членов денежного потока на 33,7 % превышает величину стартового капитала;
3) наибольшую величину показателя IRR = 27, 8 % имеет четвертый инвестиционный проект. Однако, учитывая, что банк предоставил ссуду под 18,0 % годовых, это преимущество не имеет существенного значения;
4) наименьший срок окупаемости РР = 1,79 имеет четвертый проект, но учитывая, что разница в сроках окупаемости между наибольшим значением (2,33 года) и наименьшим значением составляет чуть больше полугода, этим преимуществом можно пренебречь.
Таким образом, рассмотрев четыре инвестиционных проекта по четырем показателям, можно отдать предпочтение первому проекту.
В работах, посвященных методам экономической оценки инвестиций, отдается предпочтение показателю NPV. Объясняется это следующими факторами:
1) данный показатель характеризует прогнозируемую величину прироста капитала фирмы в случае реализации предлагаемого инвестиционного проекта;
2) проектируя использование нескольких инвестиционных проектов, можно суммировать показатели NPV каждого из них, что даст в агрегированном виде величину прироста капитала.
При анализе альтернативных инвестиционных проектов использование показателя внутренней нормы доходности - IRR. в силу ряда присущих ему недостатков должно носить ограниченный характер. Рассмотрим некоторые из них.
1. Поскольку IRR является относительным показателем, исходя из его величины, невозможно сделать вывод о размере увеличения капитала предприятия при рассмотрении альтернативных проектов. К примеру возьмем два альтернативных проекта, параметры которых представлены в таблице 3.8.
Таблица 3.8.
| Проект | Размер инвестиций | Денежный поток по годам | IRR, % | NPV при доходности 15 % тыс. |
| ций | 1 2 3 | |||
| А Б | 795 1949 | 450 570 650 800 1100 1500 | 45,0 50,0 | 455,0 565,0 |
Если судить о проектах только по показателю IRR , то проект А более предпочтителен, имеете с тем, прирост капитала он обеспечивает в меньшем размере, чем проект А.
Если фирмa имеет возможность реализовать проект Б без привлечении заемных средств, то он становится более привлекателен;
2) из определения сущности показателя IRR следует, что он показывает максимальный относительный уровень затрат, связанных с реализацией инвестиционного проекта. Следовательно, если данный показатель одинаков для двух инвестиционных проектов и он превышает "цену" инвестиций (например, банковского процента на заемный капитал, предназначенный на реализацию проектов), то для выбора между проектами необходимо использовать другие критерии;
5) показатель IRR непригоден для анализа проектов, в которых денежный поток чередуется притоком и оттоком капитала. В этом случае выводы, сделанные на основе показателя IRR могут быть не корректны.
Сравнительный анализ проектов различной продолжительности.
При сравнении проектов различной продолжительности целесообразно использовать следующую процедуру:
1) определить общее кратное для числа лет реализации каждого проекта. Например, проект А имеет продолжительность 2 года, а проект Б - 3 года, следовательно, общее кратное для этих проектов составит 6 лет, откуда можно сделать предположение, что в течение 6 лет проект А может быть повторен триады (три цикла), а проект Б - два раза (два цикла). Следовательно, проект А будет иметь три потока годовых платежей: 1-2-й год, 3-4-И год и 5-6-й год, а проект Б - два потока: I-3-й год и 3-6-й год;
2) считая, что каждый из проектов будет повторяться несколько циклов, рассчитывается суммарное значений показателя NPV для повторяющихся проектов;
5) выбрать тот проект из исходных, у которого суммарное значение NPV повторяющегося потока будет наибольшее.
Суммарное значение NPV повторяющегося потока находится по формуле:
NPV (n,y) = NPV (y) * (1 + 1/(1+j)j + 1/(1+j)n) (3.11)
где NPV (y) - чистая приведенная стоимость исходного (повторяющегося проекта;
i – продол;ительность итого проекта;
n - число повторении (циклов) исходного проекта (число слагаемые в скобках);
i - процентная ставка в долях единицы, используемая при дисконтировании (ставка предполагаемого дохода).
Пример 3.14. Имеется ряд инвестиционных проектов, требующих равную величину стартовых капиталов - 200 млн.у.д.е. "Цена" капитала, т.е. предполагаемый доход составляет 10 %. Требуется выбрать наиболее оптимальный из них, если потоки платежей (приток) характеризуются следующими данными;
проект А:100; 140;
проект Б; 60; 80; 120;
проект В:100; 144.
В таблице приведены расчеты NPV.
Таблица 3.9.
| Годы | Коэффициенты дисконтирования iL = ЮЛ | Вариант А | ||
| Цикл I Цикл 2 Цикл 5 | ||||
| Поток PV | Поток РV | Поток PV | ||
| 0 | I | -200 -200 | ||
| I | 0,909 | 100 90,9 | ||
| 2 | 0,826 | 140 115,64 | -200 -165,2 | |
| 5 | 0,751 | 100 75,1 | ||
| 4 | 0,683 | 140 95,62 | -200 -156.6 | |
| 5 | 0.621 | 100 62,1 | ||
| 6 | 0,564 | 140 78,56 | ||
| NPV | 6,54 | 5,52 | 4,46 | |
| Годы | Коэффициенты дисконтирования (I = 10 %) | Вариант Б Цикл I Цикл 2 | |||
| Поток | PV | Поток | PV | ||
| 0 | 1 | -200 | -200 | ||
| I | 0.909 | 60 | 54,54 | ||
| 2 | 0,826 | 80 | 66,08 | ||
| 5 | 0.751 | 120 | 90,12 | -200 | -150.2 |
| 4 | 0,683 | 60 | 40,98 | ||
| 5 | 0,621 | 80 | 49,68 | ||
| 6 | 0,564 | 120 | 67,68 | ||
| NPV | 10,74 | 8,14 | |||
| Годы | Коэффициенты дисконтирования i= 10% | Вариант В | |||||
| Цикл 1 | Цикл 2 | Цикл 3 | |||||
| Поток | РV | Поток | PV | Поток | PV | ||
| 0 | 1 | -200 | -200 | ||||
| I | 0.909 | 100 | 909 | ||||
| 2 | 0,826 | 144 | 118,94 | -200 | -165.2 | ||
| 5 | 0,751 | 100 | 75,1 | ||||
| 4 | 0,683 | 144 | 98,35 | -200 | -136,6 | ||
| 5> | 0.621 | 100 | 62,1 | ||||
| 6 | 0,564 | 144 | 81,2 | ||||
| NPV | 9,84 | 8.25 | 6,7 | ||||
NPVа = 6.54 + 5,52 + 4,46 = 16,52
NPVб = 10,74 + 8,14 = 18,88
NPVв = 9,84 + 8,25 + 6,7 = 24,79
Из приведенной таблицы видно, что при трехкратном повторении проекта А суммарное значение NРV составит 16,52 млн. рус. или же по формуле;
NPV = 6,54 + 6.54/(1+0.1)2 + 6.54/(1+0.1)4 = 16,52 млн.руб.
Поскольку из трех рассмотренных проектов, имеющих различную продолжительность к различные денежные потоки, наибольшее значение NPV принадлежит проекту В, то его можно считать наиболее привлекательным.
3.7. Анализ эффективности инвестиционных проектов в условиях инфляции.Инфляция искажает результаты анализа эффективности долгосрочных инвестиций. Основная причина заключается в том, что амортизационные отчисления рассчитываются, исходя из первоначальной стоимости объекта, а ни его стоимости при замене.
В результате при росте дохода одновременно с ростом инфляции увеличивается налогооблагаемая база, так как сдерживающий фактор - амортизационные отчислений остаются постоянными, вследствие чего реальные денежные потоки отстают от инфляции. Чтобы проиллюстирировать что, рассмотрим, следующий весьма условный пример.
Пример 3.15.Инвестор вложил капитал в проект, рассчитанный на четыре года при полном отсутствии инфляция и уровне налогообложения 40 %. Ожидается, что при этом будут иметь место следующие денежные потоки (тыс.у. д. е. ).
Таблица 3.10
| Год | Выручка | Текущие расходы | Амортизация | Валовая прибыль (гр.2-гр.3-гр.4) | Налоги (гр.5 х 0,4) | Чистая прибыль (гр.5 – гр.6) | Денежный поток после налогооблажения (гр.7 х гр.4) |
| 1 | 2000 | 1100 | 500 | 400 | 160 | 240 | 740 |
| 2 | 2000 | 1100 | 500 | 400 | 160 | 240 | 740 |
| 3 | 2000 | 1100 | 500 | 400 | 160 | 240 | 740 |
| 4 | 2000 | 1100 | 500 | 400 | 160 | 240 | 740 |
Рассмотрим теперь ситуацию, когда присутствует инфляция, уровень которой 7 % в год и ожидается, что денежные накопления будут расти вместе с инфляцией теми же темпами. В этом случае расчет денежных потоков представим в таблице 3.11.
Таблица 3.11.
| Год | Выручка | Текущие расходы | Амортизация | Валовая прибыль (гр.2-гр.3-гр.4) | Налоги (гр.5 х 0,4) | Чистая прибыль (гр.5 – гр.6) | Денежный поток после налогооблажения (гр.7 х гр.4) |
| 1 | 200*1,07=2140 | 1100*1,07=11,77 | 500 | 463,0 | 182,2 | 280,8 | 780,8 |
| 2 | 200*1,072=2289,8 | 1100*1,072=1259,4 | 500 | 530,4 | 212,6 | 317,8 | 817,8 |
| 3 | 200*1,073=2289,8 | 200*1,073=2289,8 | 500 | 602,6 | 241,0 | 361,6 | 861,6 |
| 4 | 200*1,074=2289,8 | 200*1,074=2289,8 | 500 | 679,7 | 271,9 | 407,8 | 907,8 |
По абсолютной величине эти потоки больше, чем рассматриваемые ранее; их необходимо продефлировать на уровень инфляции для нахождения реальной величины. После дефлирования они будут выглядеть следующий образом:
| Годы | ||||
| 1 | 2 | 3 | 4 | |
| Реальный денежный поток, тыс. у.д.е. |
|
|
|
|
Как видим, реальные денежные потоки после налогообложения уступают номинальным потокам и они устойчиво уменьшаются с течением времени. Как уже указывалось, причина в тон, что амортизационные отчисления не изменяются в зависимости от инфляции, поэтому все возрастающая часть прибыли становится объектом налогообложения. Вместе с тем, вновь отметим, что приведенный пример носит весьма условный характер, т.к. индексы инфляции на продукцию фирмы и потребляемое им сырье могут существенно отличаться от общего индекса инфляции.
Наиболее корректной является методика, предусматривающая корректировку всех факторов, влияющих на денежные потоки инвестиционных проектов.
С помощью таких пересчетов исчисляются новые денежные потоки, которые и сравниваются между собой с помощью показателя NPV.
Существуют и более простые методы. Рассмотрим их на примерах.
Пример 3.16. Инвестор вложил в ценные бумаги 10,0 млн.у.д.е. в начале года и получил по прошествии года 11,0 млн.у.д.е. Следовательно, номинально доходность этой суммы составила 10 % (11/10=1,1)
Вместе с том, если допустить, что инфляция составляла 12 % в год, то покупательная способность полученной суммы окажется ниже на (I - 1/1,12). • 100 = 10,71 %. Следовательно, реальная доходность на вложенный капитал будет также ниже. Поэтому, чтобы обеспечить желаемый реальный доход, инвестор должен был сделать вложения в бумаги с большей доходностью, а именно отличающиеся от исходной доходности на величину индекса инфляции:
1,1 • 1,12 = 1,2320.
Существует зависимость можду обычной ставкой доходности (i), ставкой доходноcти и условиях инфляции (r ) и показателем инфляции ( a)
I +r = (1 + i) • (I +a).
Упростив формулу, получим:
I +r = I +a + i + ia
r =a +i +ia. (4.12)
Величиной ia ввиду ее незначительности можно пренебречь, тогда для практических расчетов формула приобретает вид
R= i+ a
Коэффициент дисконтирования в условиях инфляции рассчитывается но формула:
1/1+r = 1/1 + i + a
Если использовать данные, приведенные в предыдущем примере, то коэффициент дисконтирования равен 1/1 + 0.1 + 0.12 = 1/1.22=0,82
Продолжим рассмотрение инвестиционных проектов в условиях инфляции.
Пример 3.17. Оценим инвестиционный проект, имеющим следующие параметры: стартовые инвестиции - 8 млн.у.д.е.; период реализации - 3 года; денежный поток по годам (у.д.е.); 4000; 4000; 5000; требуемая ставка доходности (без учета инфляции) - 18 %; среднегодовой индекс инфляции 10 %. Произведем оценку проекта без учета и с учетом инфляции. Расчет представлен в таблице 3.12.
Таблице 3.12
| Годы | Расчет без учета инфляции | Расчет с учетом инфляции (Вариант 1) | Расчет с учетом инфляции (Вариант 2) | ||||||
| Коэф-ент дисконт.по ставке, 18 % | Денежный поток, тыс. у.д.е. | Дисконтчлены денежн. потока, PV | Коэф. Дисконт с учетом инфляц. По ставке, 29,8% | Денеж. Поток, тыс. у.д.е. | Дисконтчлены денеж. потока, PV | Коэф.дискон с учетом инфляц по ставке, 28 % | Денеж.поток. тыс. у.д.е. | Дискон.члены денеж потока | |
| 0 | 1 | -8000 | -8000.0 | 1 | -8000 | -8000 | 1 | -8000 | -8000 |
| 1 | 0.8475 | 4000 | 3389.8 | 0.770 | 4000 | 3080 | 0.781 | 4000 | 3124 |
| 2 | 0.7182 | 4000 | 2872.7 | 0.593 | 4000 | 2372 | 0.610 | 4000 | 2440 |
| 3 | 0.6086 | 5000 | 3043.2 | 0.457 | 5000 | 2285 | 0.477 | 5000 | 2385 |
Как видно из расчетной таблицы, при отсутствии инфляции проект целесообразно принять, т.к. NPV= 1305,7.
Однако расчет, сделанный с учетом инфляции по двум вариантам,
хотя и дает различные значения NPV, но оба с отрицательным знаком, что свидетельствует о невыгодности принятия данного проекта.
3.8. Риск и планирование капитальных вложений.
Похожие работы
... продолжительность которого называется горизонтом расчета. Горизонт расчета измеряется количеством шагов расчета. 2. Затратный (имущественный) подход. Его сущность, область применения и этапы Подход к оценке имущества предприятия с точки зрения затрат - это определение его текущей стоимости на основе расчета восстановительной стоимости оцениваемого объекта (или стоимости замещения) и ...
... профессиональным оценщиком заказчику, в котором обосновывается проведенная оценка стоимости заказанного объекта. Глава 2. Основные подходы и методы, используемые при оценке имущества и их применение 2.1 Сущность и особенности подходов и методов оценки имущества Подход к оценке представляет собой совокупность методов оценки, объединенных общей методологией. Методом оценки является ...
... от характера финансовых вложений, порядка их приобретения и использования единицей финансовых вложений может быть серия, партия, однородная совокупность финансовых вложений. 2. Правила оценки имущества, обязательств и хозяйственных операций на примере ЗАО “Проммаш” 2.1. Краткая характеристика ЗАО “Проммаш” ЗАО “Проммаш” создано в соответствии с Указом Президента РФ от 30 декабря2005 года. ...
... , и когда оно разработано самой компанией. Поэтому, признавая нематериальные активы – активами, возникает нелегкая задача — дать по возможности наиболее обобщающие рекомендации по стоимостной оценке нематериальных активов, которые сами по себе весьма значительно отличаются друг от друга. Конечно можно выделить наиболее общие факторы, общие критерии эффективности и некоторые другие наиболее ...
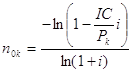 .
.
0 комментариев