Навигация
1.2 Свойства решений.
Пусть ЗПЛ представлена в следующей записи:
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
Чтобы задача (7) – (8) имела решение, системе её ограничений (8) должна быть совместной. Это возможно, если r этой системы не больше числа неизвестных n. Случай r>n вообще невозможен. При r= n система имеет единственное решение, которое будет при ![]() оптимальным. В этом случае проблема выбора оптимального решения теряет смысл. Выясним структуру координат угловой точки многогранных решений. Пусть r<n. В этом случае система векторов
оптимальным. В этом случае проблема выбора оптимального решения теряет смысл. Выясним структуру координат угловой точки многогранных решений. Пусть r<n. В этом случае система векторов ![]() содержит базис — максимальную линейно независимую подсистему векторов, через которую любой вектор системы может быть выражен как ее линейная комбинация. Базисов, вообще говоря, может быть несколько, но не более
содержит базис — максимальную линейно независимую подсистему векторов, через которую любой вектор системы может быть выражен как ее линейная комбинация. Базисов, вообще говоря, может быть несколько, но не более ![]() . Каждый из них состоит точно из r векторов. Переменные ЗЛП, соответствующие r векторам базиса, называют, как известно, базисными и обозначают БП. Остальные n – r переменных будут свободными, их обозначают СП. Не ограничивая общности, будем считать, что базис составляют первые m векторов
. Каждый из них состоит точно из r векторов. Переменные ЗЛП, соответствующие r векторам базиса, называют, как известно, базисными и обозначают БП. Остальные n – r переменных будут свободными, их обозначают СП. Не ограничивая общности, будем считать, что базис составляют первые m векторов ![]() . Этому базису соответствуют базисные переменные
. Этому базису соответствуют базисные переменные ![]() , а свободными будут переменные
, а свободными будут переменные ![]() .
.
Если свободные переменные приравнять нулю, а базисные переменные при этом примут неотрицательные значения, то полученное частное решение системы (8) называют опорным решением (планом).
Теорема. Если система векторов ![]() содержит m линейно независимых векторов
содержит m линейно независимых векторов ![]() , то допустимый план
, то допустимый план ![]() (10) является крайней точкой многогранника планов.
(10) является крайней точкой многогранника планов.
Теорема. Если ЗЛП имеет решение, то целевая функция достигает экстремального значения хотя бы в одной из крайних точек многогранника решений. Если же целевая функция достигает экстремального значения более чем в одной крайней точке, то она достигает того же значения в любой точке, являющейся их выпуклой линейной комбинацией.
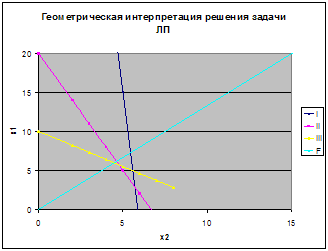
§2.Графический способ решения ЗЛП.
Геометрическая интерпретация экономических задач дает возможность наглядно представить, их структуру, выявить особенности и открывает пути исследования более сложных свойств. ЗЛП с двумя переменными всегда можно решить графически. Однако уже в трехмерном пространстве такое решение усложняется, а в пространствах, размерность которых больше трех, графическое решение, вообще говоря, невозможно. Случай двух переменных не имеет особого практического значения, однако его рассмотрение проясняет свойства ОЗЛП, приводит к идее ее решения, делает геометрически наглядными способы решения и пути их практической реализации.
Пусть дана задача
![]() (11)
(11)
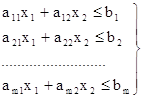 (12)
(12)
![]() (13)
(13)
Дадим геометрическую интерпретацию элементов этой задачи. Каждое из ограничений (12), (13) задает на плоскости ![]() некоторую полуплоскость. Полуплоскость — выпуклое множество. Но пересечение любого числа выпуклых множеств является выпуклым множеством. Отсюда следует, что область допустимых решений задачи (11) — (13) есть выпуклое множество.
некоторую полуплоскость. Полуплоскость — выпуклое множество. Но пересечение любого числа выпуклых множеств является выпуклым множеством. Отсюда следует, что область допустимых решений задачи (11) — (13) есть выпуклое множество.
Перейдем к геометрической интерпретации целевой функции. Пусть область допустимых решений ЗЛП — непустое множество, например многоугольник ![]() .
.
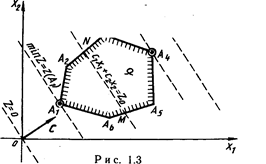
Выберем произвольное значение целевой функции ![]() . Получим
. Получим ![]() . Это уравнение прямой
линии. В точках прямой NМ целевая функция сохраняет одно и то же постоянное значение
. Это уравнение прямой
линии. В точках прямой NМ целевая функция сохраняет одно и то же постоянное значение ![]() . Считая в равенстве (11)
. Считая в равенстве (11) ![]() параметром, получим уравнение семейства параллельных прямых, называемых линиями уровня целевой функции (линиями постоянного значения).
параметром, получим уравнение семейства параллельных прямых, называемых линиями уровня целевой функции (линиями постоянного значения).
Найдём частные производные целевой функции по ![]() и
и ![]()
![]() (14)
(14)
![]() (15)
(15)
Частная производная (14)
((15)) функции показывает скорость ее возрастания вдоль данной оси. Следовательно, ![]() и
и ![]() — скорости возрастания
— скорости возрастания ![]() соответственно вдоль осей
соответственно вдоль осей ![]() и
и ![]() . Вектор
. Вектор ![]() называется градиентом функции. Он показывает направление наискорейшего возрастания целевой функции:
называется градиентом функции. Он показывает направление наискорейшего возрастания целевой функции:
![]()
Вектор —![]() указывает направление наискорейшего убывания целевой функции. Его называют антиградиентом.
указывает направление наискорейшего убывания целевой функции. Его называют антиградиентом.
Вектор ![]() перпендикулярен к прямым
перпендикулярен к прямым ![]() семейства
семейства ![]()
Из геометрической интерпретации элементов ЗЛП вытекает следующий порядок ее графического решения.
1. С учетом системы ограничений строим область допустимых решений ![]()
2. Строим вектор ![]() наискорейшего возрастания целевой функции — вектор градиентного направления.
наискорейшего возрастания целевой функции — вектор градиентного направления.
3. Проводим произвольную линию уровня ![]()
4. При решении задачи на максимум перемещаем линию уровня ![]() в направлении вектора
в направлении вектора ![]() так, чтобы она касалась области допустимых решений в ее крайнем положении (крайней точке). В случае решения задачи на минимум линию уровня
так, чтобы она касалась области допустимых решений в ее крайнем положении (крайней точке). В случае решения задачи на минимум линию уровня ![]() перемещают в антиградиентном направлении
перемещают в антиградиентном направлении
5. Определяем оптимальный план ![]() и экстремальное значение целевой функции
и экстремальное значение целевой функции ![]() .
.
§3.Симплексный метод.
Общая идея симплексного метода (метода последовательного улучшения плана) для решения ЗЛП состоит
1) умение находить начальный опорный план;
2) наличие признака оптимальности опорного плана;
3) умение переходить к нехудшему опорному плану.
Пусть ЗЛП представлена системой ограничений в каноническом виде:
![]() .
.
Говорят, что ограничение ЗЛП имеет предпочтительный вид, если при неотрицательной правой части ![]() левая часть ограничений содержит переменную, входящую с коэффициентом, равным единице, а в остальные ограничения равенства - с коэффициентом, равным нулю.
левая часть ограничений содержит переменную, входящую с коэффициентом, равным единице, а в остальные ограничения равенства - с коэффициентом, равным нулю.
Пусть система ограничений имеет вид
![]()
Сведем задачу к каноническому виду. Для этого прибавим к левым частям неравенств дополнительные переменные ![]()
![]() . Получим систему, эквивалентную исходной:
. Получим систему, эквивалентную исходной:
![]() ,
,
которая имеет предпочтительный вид
![]() .
.
В целевую функцию дополнительные переменные вводятся с коэффициентами, равными нулю ![]()
![]() .
.
Пусть далее система ограничений имеет вид
![]()
Сведём её к эквивалентной вычитанием дополнительных переменных ![]()
![]() из левых частей неравенств системы. Получим систему
из левых частей неравенств системы. Получим систему
![]()
Однако теперь система ограничений не имеет предпочтительного вида, так как дополнительные переменные ![]() входят в левую часть (при
входят в левую часть (при ![]() ) с коэффициентами, равными –1. Поэтому, вообще говоря, базисный план
) с коэффициентами, равными –1. Поэтому, вообще говоря, базисный план ![]() не является допустимым. В этом случае вводится так называемый искусственный базис. К левым частям ограничений-равенств, не имеющих предпочтительного вида, добавляют искусственные переменные
не является допустимым. В этом случае вводится так называемый искусственный базис. К левым частям ограничений-равенств, не имеющих предпочтительного вида, добавляют искусственные переменные ![]() . В целевую функцию переменные
. В целевую функцию переменные ![]() , вводят с коэффициентом М в случае решения задачи на минимум и с коэффициентом -М для задачи на максимум, где М - большое положительное число. Полученная задача называется М-задачей, соответствующей исходной. Она всегда имеет предпочтительный вид.
, вводят с коэффициентом М в случае решения задачи на минимум и с коэффициентом -М для задачи на максимум, где М - большое положительное число. Полученная задача называется М-задачей, соответствующей исходной. Она всегда имеет предпочтительный вид.
Пусть исходная ЗЛП имеет вид
![]() (1)
(1)
![]() (2)
(2)
![]()
![]() (3)
(3)
причём ни одно из ограничений не имеет предпочтительной переменной. М-задача запишется так:
![]() (4)
(4)
![]() (5)
(5)
![]()
![]() ,
, ![]() ,
, ![]() (6)
(6)
Задача (4)-(6) имеет предпочтительный план. Её начальный опорный план имеет вид
![]()
Если некоторые из уравнений (2) имеют предпочтительный вид, то в них не следует вводить искусственные переменные.
Теорема. Если в оптимальном плане
![]() (7)
(7)
М-задачи (4)-(6) все искусственные переменные ![]()
![]() , то план
, то план ![]() является оптимальным планом исходной задачи (1)-(3).
является оптимальным планом исходной задачи (1)-(3).
Для того чтобы решить задачу с ограничениями, не имеющими предпочтительного вида, вводят искусственный базис и решают расширенную М-задачу, которая имеет начальный опорный план ![]()
Решение исходной задачи симплексным методом путем введения искусственных переменных ![]() называется симплексным методом с искусственным базисом.
называется симплексным методом с искусственным базисом.
Если в результате применения симплексного метода к расширенной задаче получен оптимальный план, в котором все искусственные переменные ![]() , то его первые n компоненты дают оптимальный план исходной задачи.
, то его первые n компоненты дают оптимальный план исходной задачи.
Теорема. Если в оптимальном плане М-задачи хотя бы одна из искусственных переменных отлична от нуля, то исходная задача не имеет допустимых планов, т. е. ее условия несовместны.
Похожие работы
... во многих экономических задачах, приводит к линейной функции с линейными ограничениями, наложенными на неизвестные. 2. Области применения и ограничения использования линейного программирования для решения экономических задач Особенно широкое применение методы и модели линейного программирования получили при решении задач экономии ресурсов (выбор ресурсосберегающих технологий, составление ...
... строки и каждого столбца таблицы (матрицы) определяют специальные числа, называемые потенциалами. С помощью этих потенциалов можно установить, нужно ли заполнять свободную клетку матрицы или ее нужно оставить незаполненной. Для решения задач методом потенциалов исходный план должен иметь количество заполненных клеток m + n – 1 (m - число строк, n - число столбцов). Если план не отвечает этим ...
... рулонов, при котором все поступающие специальные заявки будут выполнены при минимальных затратах бумаги. Графический метод решения задач линейного программирования 1. Область решений линейных неравенств. Пусть задано линейное неравенство с двумя переменными и (1) Если величины и рассматривать как координаты точки плоскости, то совокупность точек ...
... разрабатываются методы отыскания экстремальных значений целевой функции среди множества ее возможных значений, определяемых ограничениями. Наличие ограничений делает задачи математического программирования принципиально отличными от классических задач математического анализа по отысканию экстремальных значений функции. Методы математического анализа для поиска экстремума функции в задачах ...

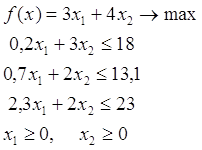
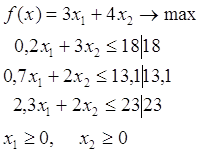
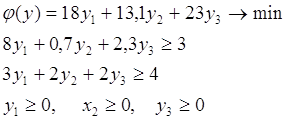
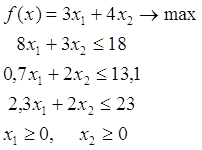
0 комментариев