Навигация
5.2 Задача о смесях.
В различных отраслях народного хозяйства возникает проблема составления таких рабочих смесей на основе исходных материалов, которые обеспечивали бы получение конечного продукта, обладающего определенными свойствами. К этой группе задач относятся задачи о выборе диеты, составлении кормового рациона в животноводстве, шихт в металлургии, горючих и смазочных смесей в нефтеперерабатывающей промышленности, смесей для получения бетона в строительстве и т. д. Высокий уровень затрат на исходные сырьевые материалы и необходимость повышения эффективности производства выдвигает на первый план следующую задачу: получить продукцию с заданными свойствами при наименьших затратах на исходные сырьевые материалы.
5.3 Задача о раскрое материалов.
Сущность задачи об оптимальном раскрое состоит в разработке таких технологически допустимых планов раскроя, при которых получается необходимый комплект заготовок, а отходы (по длине, площади, объему, массе или стоимости) сводятся к минимуму. Рассмотрим простейшую модель раскроя по одному измерению. Более сложные постановки ведут к задачам целочисленного программирования.
5.4 Транспортная задача.
Рассмотрим простейший вариант модели транспортной задачи, когда речь идет о рациональной перевозке некоторого однородного продукта от производителей к потребителям; при этом имеется баланс между суммарным спросом потребителей и возможностями поставщиков по их удовлетворению. Причем потребителям безразлично, из каких пунктов производства будет поступать продукция, лишь бы их заявки были полностью удовлетворены. Так как от схемы прикрепления потребителей к поставщикам существенно зависит объем транспортной работы, возникает задача о наиболее рациональном прикреплении, правильном направлении перевозок грузов, при котором потребности полностью удовлетворяются, вся продукция от поставщиков вывозится, а затраты на транспортировку минимальны.
5.5 Задача о размещении заказа.
Речь идет о задаче распределения заказа (загрузки взаимозаменяемых групп оборудования) между предприятиями (цехами, станками, исполнителями) с различными производственными и технологическими характеристиками, но взаимозаменяемыми в смысле выполнения заказа. Требуется составить план размещения заказа (загрузки оборудования), при котором с имеющимися производственными возможностями заказ был бы выполнен, а показатель эффективности достигал экстремального значения.
§7. Анализ задачи об оптимальном использовании сырья.
Исходя из специализации и своих технологических возможностей предприятие может выступать четыре вида продукции. Сбыт любого количества обеспечен. Для изготовления этой продукции используются трудовые ресурсы, полуфабрикаты и станочное оборудование. Общий объём ресурсов, расход каждого ресурса за единицу продукции, приведены в таблице 1. Требуется определить план выпуска, доставляющий предприятию максимум прибыли. Выполнить после оптимизационный анализ решения и параметров модели.
| Ресурсы | Выпускаемая продукция | Объём Ресурсов | |||||||
|
|
|
|
| ||||||
|
| Трудовые ресурсы, чел-ч | 4 | 2 | 2 | 8 | 4800 | |||
|
| Полуфабрикаты, кг | 2 | 10 | 6 | 0 | 2400 | |||
|
| Станочное оборудование, станко-ч | 1 | 0 | 2 | 1 | 1500 | |||
| Цена единицы продукции, р. | 65 | 70 | 60 | 120 |
| ||||
Решение.
Пусть ![]() - объёмы продукции
- объёмы продукции ![]() планируемый к выпуску;
планируемый к выпуску; ![]() - сумма ожидаемой выручки.
- сумма ожидаемой выручки.
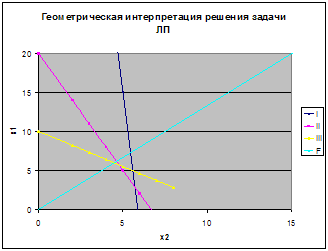
Математическая модель пря мой задачи:
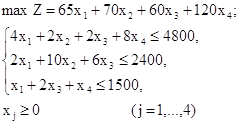
Математическая модель двойственной задачи:
![]()
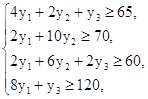
![]()
По условиям примера найти:
Похожие работы
... во многих экономических задачах, приводит к линейной функции с линейными ограничениями, наложенными на неизвестные. 2. Области применения и ограничения использования линейного программирования для решения экономических задач Особенно широкое применение методы и модели линейного программирования получили при решении задач экономии ресурсов (выбор ресурсосберегающих технологий, составление ...
... строки и каждого столбца таблицы (матрицы) определяют специальные числа, называемые потенциалами. С помощью этих потенциалов можно установить, нужно ли заполнять свободную клетку матрицы или ее нужно оставить незаполненной. Для решения задач методом потенциалов исходный план должен иметь количество заполненных клеток m + n – 1 (m - число строк, n - число столбцов). Если план не отвечает этим ...
... рулонов, при котором все поступающие специальные заявки будут выполнены при минимальных затратах бумаги. Графический метод решения задач линейного программирования 1. Область решений линейных неравенств. Пусть задано линейное неравенство с двумя переменными и (1) Если величины и рассматривать как координаты точки плоскости, то совокупность точек ...
... разрабатываются методы отыскания экстремальных значений целевой функции среди множества ее возможных значений, определяемых ограничениями. Наличие ограничений делает задачи математического программирования принципиально отличными от классических задач математического анализа по отысканию экстремальных значений функции. Методы математического анализа для поиска экстремума функции в задачах ...

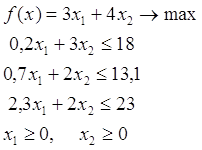
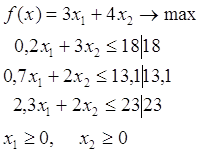
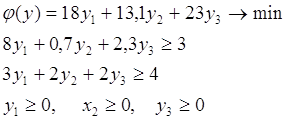
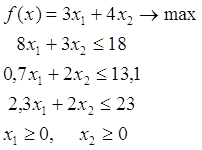
0 комментариев