Навигация
Исследование распределения температуры в тонком цилиндрическом стержне
Курсовая работа по информатике
Исполнитель: Солнцев П.В.
Санкт-Петербургский Государственный Технологический Институт (Технический Университет)
Санкт-Петербург 2001
Введение
В решении любой прикладной задачи можно выделить три основных этапа: построение математической модели исследуемого объекта, выбор способа и алгоритма решения полученной модели, численная реализация алгоритма.
Цель данной работы – на примере исследования распределения температуры в тонком цилиндрическом стержне освоить основные методы приближённых вычислений, приобрести практические навыки самостоятельных исследований, существенно опирающихся на использование методов прикладной математики.
Постановка задачи
Физическая модель
В ряде практических задач возникает необходимость исследования распределения температуры вдоль тонкого цилиндрического стержня, помещённого в высокотемпературный поток жидкости или газа. Это исследование может проводиться либо на основе обработки эксперимента (измерение температуры в различных точках стержня), либо путём анализа соответствующей математической модели.
В настоящей работе используются оба подхода.
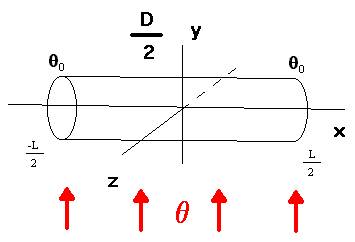
Тонкий цилиндрический стержень помещён в тепловой поток с постоянной температурой , на концах стержня поддерживается постоянная температура 0.
1.2 Математическая модель
Совместим координатную ось абсцисс с продольной осью стержня с началом в середине стержня. Будем рассматривать задачу (распределения температуры по стержню) мосле момента установления режима Т0.
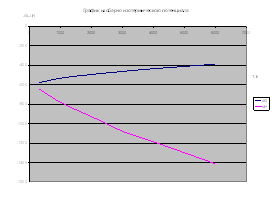
Первая математическая модель использует экспериментальные данные, при этом измеряют температуру Ui стержня в нескольких точках стержня с координатами xi. Результаты измерения Ui рассматривают как функцию регрессии и получают статистики. Учитывая чётность U(x) можно искать её в виде многочлена по чётным степеням x (ограничимся 4-ой степенью этого многочлена).
(1.1)
Задача сводится к отысканию оценок неизвестных параметров, т.е. коэффициентов a0 , a1 и a2 , например, методом наименьших квадратов.
Вторая математическая модель, также использующая экспериментальные данные, состоит в применении интерполяционных формул и может употребляться, если погрешность измерений температуры Ui пренебрежимо мала, т.е. можно считать, что U(xi)=Ui
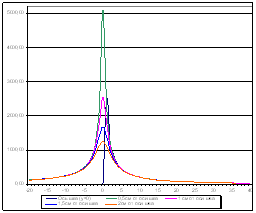
Третья математическая модель основана на использовании закона теплофизики. Можно доказать, что искомая функция U(x) имеет вид:
(1.2)
где коэффициент теплопроводности, коэффициент теплоотдачи, D – диаметр стержня, температура потока, в который помещён стержень.
Ищем U(x) как решение краевой задачи для уравнения (1.2) с граничными условиями:
(1.3)
на отрезке [-L|/2;L/2], где L – длина стержня, постоянная температура, поддерживаемая на концах стержня.
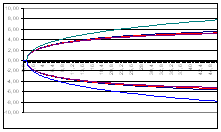
Коэффициент теплопроводности зависит от температуры:
(1.4)
где начальное значение коэффициента теплопроводности, вспомогательный коэффициент.
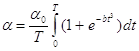 |
Коэффициент теплоотдачи вычисляют по формуле:
(1.5)
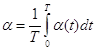 | |||
т.е. как среднее значение функции
за некоторый отрезок времени от 0 до Т, здесь значение при t стремящемся к бесконечности, b – известный коэффициент.
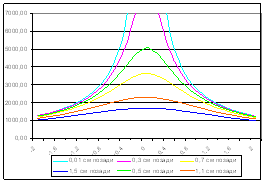
Время Т0, по истечении которого распределение температуры в стержне можно считать установившимся определяется по формуле:
(1.6)
где а – коэффициент температуропроводности, наименьший положительный корень уравнения:
(1.7)
Задание курсовой работы
Вариант № 136
Исходные данные:
L = 0.0386 м
D = 0,00386 м
оС
оС
141,85 (Вт/м*К)
2,703*10-4
6,789*10-7
3,383*102 (Вт/м2*К)
218 оС
А = 3,043*10-5 (м2/с)
11
| X, м | U, oC |
| 0 | 353 |
| 0,00386 | 343 |
| 0,00772 | 313 |
| 0,01158 | 261 |
| 0,01544 | 184 |
| 0,01930 | 74 |
Похожие работы
... Автору дипломной работы было предложено продолжить исследования электропроводности продуктов детонации. Основной задачей являлось перейти к изучению распределения электропроводности конденсированных взрывчатых веществ за фронтом пересжатой детонации. Объектом исследования выбраны такие взрывчатые вещества как октоген, гексоген, тэн и тотил. Цель исследований – получить информацию, способную ...
... в его средней части. Таким образом, можно считать, что распределение температуры в образце является достаточно равномерным, а это свидетельствует о равномерности температуры в центральной зоне самой печи. 2.2 Исследование деформации и ползучести керамических материалов 2.2.1 Керамических материалов трубчатых изделий Деформация при нагреве. С целью установления предельной температуры эксплуатации ...
... свариваемого металла, конструкцией сварного соединения, режимом сварки и начальной температурой изделия. Рекомендуется подогрев и последующая термообработка. Способы сварки: РД, РАД, АФ, КТ. 2. Исследование процессов взаимодействия между металлом, газом и шлаком 2.1 Характеристика защиты металла от взаимодействия с окружающей средой Сварка плавлением - высокотемпературный процесс, ...
... неоднородность имеет значительную глубину. Прибор интерференционно-теневой ИАБ-458 Прибор интерференционно-теневой ИАБ-458 предназначен для качественных и количественных исследований теневым методом неоднородностей оптически прозрачных сред. В приборе реализуются следующие методы исследования: светящейся точки, щели и ножа, щели и нити, сдвиговой интерферометрии и голографии. На рис. 2.4 ...

0 комментариев