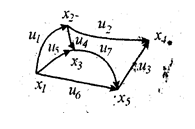
Построить остовное дерево минимальной стоимости для связанного взвешенного графа, используя алгоритм Краскала

4. Построить остовное дерево минимальной стоимости для связанного взвешенного графа, используя алгоритм Краскала.

#include <iostream.h>

#include <stdio.h>

#include <conio.h>

FILE* fi = fopen("k_graph.txt","r"); //Входной файл

FILE* fo = fopen("k_ostov.txt","w"); //Выходной файл

struct edge{ // Структура для хранения ребра

int beg,end;

int weigh;

};

edge *E; // массив с ребрами

edge *SST; //остов

int num_edge; //количество ребер в остове

int n; //количество ребер

bool *nov; //признак прохода вершины

void sort(edge *arr){ //сортировка ребер по весу

edge tmp;

for(int i=0;i<n-1;i++)

for(int j=n-1;j>i;j--)

if(arr[j].weigh<arr[j-1].weigh){

tmp = arr[j-1]; arr[j-1] = arr[j]; arr[j] = tmp;

}

}

int smezh(int v1,edge v2){

//определяет вершину смежную с v1 через ребро v2

if(v1==v2.beg)return(v2.end);

else if(v1==v2.end)return(v2.beg);

else return -1; // вершина v1 и ребро v2 не инцидентны

}

bool cycle(int v,int v0){ //определяет наличие цикла

nov[v] = 0; // v пройдена

for(int i=0;i<num_edge-1;i++)

if(smezh(v,SST[i])!=-1) //если смежны

if(smezh(v,SST[i])==v0)return 1; //из конца ребра пришли в начало

else if(nov[smezh(v,SST[i])]) // новая вершина

if(cycle(smezh(v,SST[i]),v0))return 1;

nov[v] = 1; //возвращаемся назад

return 0;

}

void kruskal(){

num_edge = 0; //остов пуст

sort(E); // упорядочивание E по возрастанию веса

for(int i=0;i<n;i++){

SST[num_edge] = E[i]; num_edge++; //добавляем ребро

// если появляется цикл - удаляем

if(cycle(SST[num_edge-1].end,SST[num_edge-1].beg))num_edge--;

for(int i=0;i<n;i++)nov[i]=1;

}

}

void out(edge *mas,int num){ // вывод ребер

int sum=0;

fprintf(fo,"%dn",num); // количество ребер

for(int i=0;i<num;i++){

fprintf(fo,"%d %d %3dn",mas[i].beg,mas[i].end,mas[i].weigh);

sum+=mas[i].weigh;

}

fprintf(fo,"%s%d","Вес найденного остова: ",sum);

}

int main(){

fscanf(fi,"%d",&n); //считываем количество ребер

E = new edge[n];

SST = new edge[n];

nov = new bool[n+1];

for(int i=0;i<n;i++)nov[i] = 1;

for(int i=0;i<n;i++) //заполняем множество ребер

fscanf(fi,"%d%d%d3",&E[i].beg,&E[i].end,&E[i].weigh);

kruskal(); //строим остов

out(SST,num_edge); //выводим в файл

return 0;

}

5.Для заданного неориентированного графа найдите максимальное паросочетание.

#include <iostream.h>

#include <stdio.h>

#include <conio.h>

FILE* fi = fopen("m_graph.txt","r");

FILE* fo = fopen("m_par.txt","w");

struct edge{ // ребро графа

int b,e;

};

int n; //количество ребер

edge *graph; // массив ребер

edge *matching; // паросочетание

int num_mat; //количество паросочетаний

bool smezh(edge q1,edge q2){ // 1 - если q1 и q2 смежны, иначе -0

return q1.b==q2.b||q1.b==q2.e||q1.e==q2.b||q1.e==q2.e;

}

void out(edge *m,int num){

fprintf(fo,"%dn",num); // количество ребер

for(int i=0;i<num;i++)

fprintf(fo,"%d %dn",m[i].b,m[i].e);

}

bool bad(){//возвращает 1, если в паросочетании есть смежное ребро

for(int i=0;i<num_mat-1;i++)

if(smezh(matching[i],matching[num_mat-1]))return 1;

return 0;

}

void solve(){ //находит максимальное паросочетание

num_mat = 0;

for(int i=0;i<n;i++){

matching[num_mat]=graph[i];num_mat++; // добавляем ребро

if(bad())num_mat--; // если уже есть смежные - удаляем

}

}

int main(){

fscanf(fi,"%d",&n);

graph = new edge[n];

matching = new edge[n];

for(int i=0;i<n;i++)

fscanf(fi,"%d%d",&graph[i].b,&graph[i].e);

solve();

out(matching,num_mat);

fcloseall();

return 0;

}

Приложение Б

Примеры входных и выходных файлов

1.

Входной файл "g_graph.txt":

5

0 0 1 1 0

0 0 0 1 1

1 0 0 0 1

1 1 0 0 0

0 1 1 0 0

Выходной файл "g_cycle.txt":

0 2 4 1 3 0

0 3 1 4 2 0

2.

Входной файл " e_graph.txt ":

5

0 1 1 1 1

1 0 1 1 1

1 1 0 1 1

1 1 1 0 1

1 1 1 1 0

Выходной файл "e_cycle.txt":

1 4 3 2 4 0 3 1 2 0 1

3.

Входной файл " p_graph.txt ":

9

0 4 5 2 0 0 0 0 0

4 0 7 0 0 0 6 0 0

5 7 0 3 0 0 0 0 0

2 0 3 0 0 0 0 0 0

0 0 0 0 0 7 8 0 0

0 0 0 0 7 0 1 0 0

0 6 0 0 8 1 0 3 1

0 0 0 0 0 0 3 0 2

0 0 0 0 0 0 1 2 0

Выходной файл "p_ostov.txt":

8

0 3 2

3 2 3

0 1 4

1 6 6

6 5 1

6 8 1

8 7 2

5 4 7

Вес найденного остова: 26

4.

Входной файл " k_graph.txt ":

5

0 1 1

1 2 2

2 3 1

0 3 4

1 3 2

Выходной файл "k_ostov.txt":

3

0 1 1

2 3 1

1 2 2

Вес найденного остова: 4

5.

Входной файл " m_graph.txt ":

7

0 1

1 4

0 3

3 2

1 3

2 0

2 5

Выходной файл "m_par.txt":

2

0 1