Навигация
Московский государственный
Горный университет
Курсовой проект по исследованию операций.
Решение задачи методами линейного,
целочисленного, нелинейного и динамического
программирования.
Выполнил студент группы
ПМ – 1 – 97 Солодовников Д. А.
Научный руководитель: Багрова Г.И.
Москва 1999 г.
Содержание:
Цель курсовой работы ……………………………………………………………..3
Линейное программирование ……………………………………………………..4
Решение задачи методом линейного программирования ……………………….6
Целочисленное линейное программирование …………………………………...9
Решение задачи методом целочисленного линейного программирования …...10
Нелинейное программирование ………………………………………………….15
Решение задачи нелинейного программирования ………………………………15
Динамическое программирования ………………………………………………..20
Решение задачи динамического программирования …………………………….21
Графическая интерпретация решений ……………………………………………25
Трудоемкость и эффективность решения модели различными методами …….27
О проекте …………………………………………………………………………...28
Цель курсовой работы.
Решить задачу методами линейного, целочисленного, нелинейного и динамического программирования. Сопоставить трудоемкость и эффективность решения модели различными методами.
Задание:
Определить плановые задания добывающим предприятиям, если в работе находится N = 12 составов.
Цена готовой продукции 50 у.е. за тонну.
Руда, поступающая на обогатительную фабрику должна иметь содержание 29,8 – 29,9%.
| Наименование показателя | Единицы Измерения | Предприятия | ||
| 1 |
2 | 3 | ||
| Max добыча ПИ | тыс. тонн | 740 | 680 | 600 |
| Содержание полезного компонента | % | 29,1 | 29,8 | 30,8 |
| Извлечение | % | 80 | 75 | 70 |
| Затраты на добычу, транс-портировку и переработку | у.е. /т | 6 | 7 | 8 |
| Производительность Состава | тыс. тонн | 120 | 110 |
106 |
| Коэффициент увеличения затрат при нагрузке: До 30% - 31 – 50% - 51 – 70% - 71 – 100%- максимальной | 1,8 1,7 1,6 1,4 1 | 1,7 1,5 1,4 1,2 1 | 1,9 1,7 1,6 1,3 1 | |
В курсовом проекте введены следующие условные обозначения:
ЛП – линейное программирование;
ЦЛП – целочисленное линейное программирование;
ДП - динамическое программирование.
Линейное программирование.
Основная задача линейного программирования:
Найти неотрицательное решение системы ограничений (1,2) обеспечивающее максимум (минимум) целевой функции.
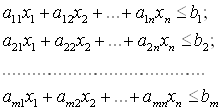
1) Первый канонический вид:
a11x1+a12x2+…+a1jxj+…+a1nxn![]() b1
b1
a21x1+a22x2+…+a2jxj+…+a2nxn![]() b2
b2
……………………………………
ai1x1 +ai2x2+…+aijxj +…+ ainxn![]() bi
bi
.……………………………………
am1x1+am2x2+…+amjxj+…+amnxn![]() bn
bn
![]()
![]() xj
xj![]() 0; j=1,n; i=1,m;
0; j=1,n; i=1,m;
Z=C1x1+C2x2+…+Cjxj+…+Cnxn![]() max (min);
max (min);
2) Второй канонический вид:
a11x1+a12x2+…+a1jxj+…+a1nxn+y1=b1
a21x1+a22x2+…+a2jxj+…+a2nxn+y2=b2
………………………………………
ai1x1 +ai2x2+…+aijxj +…+ ainxn+yi=bi
.………………………………………
am1x1+am2x2+…+amjxj+…+amnxn+ym=bn
![]()
![]() xj
xj![]() 0; j=1,n; i=1,m;
0; j=1,n; i=1,m;
Z=C1x1+C2x2+…+Cjxj+…+Cnxn![]() max (min);
max (min);
Чтобы решить задачу линейного программирования необходимо привести ее к каноническому виду.
Теоремы линейного програмирования:
Теорема 1. Множество допустимых решений основной задачи линейного программирования выпукло.
Теорема 2. Линейная функция задачи линейного программирования достигает своего экстремального значения в крайней точке множества решений.
При решении системы ограничений могут возникнуть следующие случаи:
1) Система ограничений несовместна, поэтому отыскать оптимальное решение невозможно (рис. 1.1).
2) Система ограничений имеет единственное решение ( рис. 1.2).
3) Система ограничений имеет конечное число решений (имеется замкнутая область допустимых решений). Оптимальное решение отыскивается среди решений, принадлежащих данной области(рис. 1.3).
4) Система ограничений имеет бесчисленное множество решений (рис. 1.4).
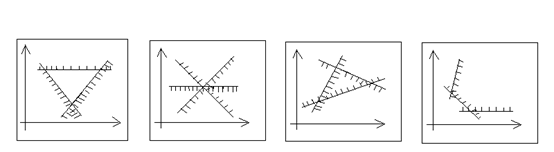
Рис. 1.1 Рис. 1.2 Рис. 1.3 Рис. 1.4

![]()
![]()
![]()
C
a b
![]()
![]()
Рис. 2
Симплекс – метод.
Решение задачи линейного программирования включает в себя 3 этапа:
1) Отыскание базисного решения – некой точки А (рис. 2) лежащей на функции.
2) Отыскание опорного решения – некой точки B (рис. 2) принадлежащей области, образованной ограничениями.
3) Отыскание оптимального решения – некой точки С (рис. 2) принадлежащей той – же области, и в которой целевая функция достигает своего экстремума.
Отыскание оптимального решения с использованием симплекс – метода сводится к последовательному направленному перебору вершин многогранника, образованного ограничениями при котором монотонно увеличивается (уменьшается) значение целевой функции.
В настоящее время решение задач ЛП с помощью симплекс – метода реализуется с помощью ЭВМ.
Решение задачи методом линейного программирования.
Симплекс – метод.
Определить плановое задание добывающим предприятиям, если в работе находится N=12 составов. Цена готовой продукции 50 у.е. за тонну. Руда поступающая на обогатительную фабрику должна иметь содержание Ме (полезного компонента) в пределах 29,9 – 29,9 %
| Наименование показателя | Единицы Измерения | Предприятия | ||
| 1 |
2 | 3 | ||
| Max добыча ПИ | тыс. тонн | 740 | 680 | 600 |
| Содержание полезного компонента | % | 29,1 | 29,8 | 30,8 |
| Извлечение | % | 80 | 75 | 70 |
| Затраты на добычу, транс-портировку и переработку | у.е. /т | 6 | 7 | 8 |
| Производи-тельность Состава | тыс. тонн | 120 | 110 |
106 |
x1, x2, x3 – количество составов выделенных соответственно предприятиям 1, 2 и 3.
Ограничения:
· По количеству составов:
![]() ,
,
где n – количество предприятий, N – количество составов.
1. x1 + x2 + x3![]() 12
12
· По максимальному объему добычи руды с каждого из предприятий:
![]() , где
, где ![]()
2. 120x1 ![]() 740 или x1
740 или x1![]() 6,16666 (для предприятия 1);
6,16666 (для предприятия 1);
3. 110x2![]() 680 или x2
680 или x2![]() 6,18181 (для предприятия 2);
6,18181 (для предприятия 2);
4. 106x3 ![]() 600 или x3
600 или x3![]() 5,6603 (для предприятия 3).
5,6603 (для предприятия 3).
· По содержанию полезного компонента в руде:
по формуле:
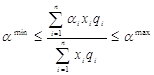
где
amin – минимально допустимое содержание полезного компонента в руде,
amax – максимально допустимое содержание полезного компонента в руде,
ai – содержание полезного компонента в руде i – того предприятия,
qi – производительность состава i – того предприятия,
имеем:
![]()
![]()
![]()
![]() Упростим неравенства 5, 6:
Упростим неравенства 5, 6:
5. 34,92x1 + 32,78x2 + 32,648x3 – 35,76x1 – 32,78x2 – 31,588x3![]() 0
0
-0,84x1 + 1,06x3![]() 0; (ограничение по минимально допустимому содержанию
0; (ограничение по минимально допустимому содержанию
полезного компонента в руде);
6. 34,92x1 + 32,78x2 + 32,648x3 – 35,88x1 – 32,89x2 – 31,694x3![]() 0
0
-0,96x1 – 0,11x2 + 0,954x3![]() 0
0
0,96 x1 + 0,11x2 – 0,954x3![]() 0; (ограничение по максимально допустимому содержанию полезного компонента в руде);
0; (ограничение по максимально допустимому содержанию полезного компонента в руде);
Целевая функция:
![]()
![]() , где
, где ![]() - цена готовой продукции (у.е. за тонну);
- цена готовой продукции (у.е. за тонну);
![]()
![]()
Z = 676800x1 + 459250x2 + 294660x3![]()
Или в тыс. тонн:
Z = 676,8x1 + 459,25x2 + 294,66x3![]()
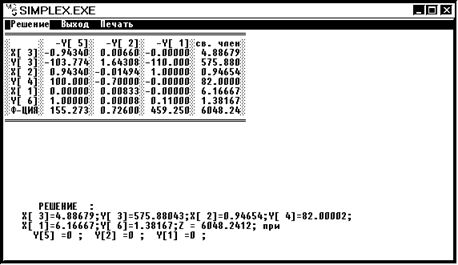
![]()
Вывод:
В результате решения данной задачи было получено значение целевой функции Z = 6048,2412;
x1 = 6,16667 – количество составов для предприятия 1;
x2 = 0,94654 – количество составов для предприятия 2;
x3 = 4,88679 – количество составов для предприятия 3;
Для получения наибольшей выгоды (целевая функция стремящаяся к максимуму достигает своего экстремума) необходимо выполнение предприятиями следующего плана:
Предприятие 1 - Р(план) = 740 – y2 = 740 – 0 = 740 тыс. тонн,
Предприятие 2 – Р(план) = 680 – y3 = 680 – 575,88043 = 104,11957 тыс. тонн,
Предприятие 3 – Р(план) = 600 – y4 = 600 – 82,00002 = 517,99998 тыс. тонн.
Целочисленное линейное программирование.
При решении некоторых задач линейного программирования бывает необходимо получить целочисленное решение, которое находится методами целочисленного линейного программирования.
Задача целочисленного линейного программирования это задача, где некоторые или все переменные должны принимать строго целочисленные значения, а целевая функция и ограничения – линейные.
В некоторых задачах целочисленные значения могут быть равны только 0 или 1, тогда такие задачи называются задачами с булевыми переменными.
Задачу целочисленного линейного программирования можно решить как задачу линейного программирования, а затем округлить полученное решение. Однако такой способ допустим только при условии, что значения переменных настолько большие, что погрешностью, вызываемой округлением можно пренебречь. Если же в результате решения переменная принимает малое значение, то ее округление может привести к очень далекому от оптимального решения. Применяются два способа решения задач ЦЛП – метод отсечений и метод ветвей и границ.
Решение задачи ЦЛП методом отсечения:
1. Решение задачи как задачи ЛП.
2. Если мы получили целочисленное решение, то оно и является решением задачи ЦЛП.
3. Если мы получаем нецелочисленное решение, то мы к системе ограничений задачи ЛП прибавляем такое ограничение, что полученное нецелочисленное оптимальное решение не может содержаться во множестве допустимых решений и, таким образом, формируем новую задачу ЛП и решаем ее. Цикл повторяется до тех пор пока не будет получено целочисленное решение (решение задачи ЦЛП (если оно существует)).
Решение задачи ЦЛП методом ветвей и границ:
Похожие работы
... , 6) сетевого планирования и управления, 7) выбора маршрута, 8) комбинированные. Из перечисленных выше методов математического программирования наиболее развитым и законченным является линейное программирование. В его рамки укладывается широкий круг задач исследования операций. Линейное программирование Несмотря на требование линейности целевой функции и ограничений, в рамки линейного ...
... -бухгалтер должен: а) потребовать недостающие материалы у проверяемой организации; б) составить сообщение о невозможности дачи заключения; в) заявить письменное ходатайство о предоставлении ему дополнительных документов. 1. Исследование операций по заработной плате Задачей судебно-бухгалтерской экспертизы при исследовании операций по труду и заработной плате является активизация ...
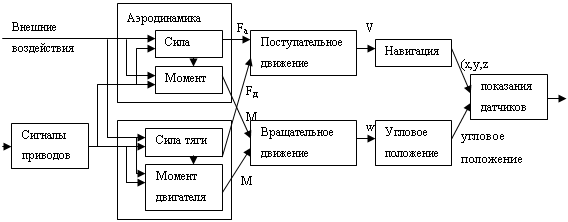
... и направление ветра, плотность воздуха и др. 4. Эквифинальность. Рано или поздно, самолет вынужден будет приземлится или разобьется. Т.о. скорости, ускорения, моменты и силы будут равны нулю. Исследование операций Задача 1 Авиакомпания «Небесный грузовик», обслуживающая периферийные районы страны, располагает А1 самолетами типа 1, А2 самолетами типа 2, А3 самолетами типа 3, которые она ...
... Лагранжа: L(x,u)=F(x)+u1g1(x)+u2g2(x)=-2x12-x22-4x1x2+6x1+1,5x2+u1 (2,5x1-x2–7)+ u2 (3x1+2,5x2-13). Получим уравнения седловой точки, применяя теорему Куна-Таккера: i=1;2 Объединим неравенства в систему А, а равенства в систему В: Система А: Система В: Перепишем систему А: 6-4x1-4x2+2,5u1+3u2 <0 1,5-4x1-2x2-u1+2,5u2 <0 2,5x1-x2–7³0 3x1+2,5x2–13³0 4)Введем новые ...
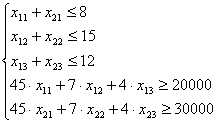
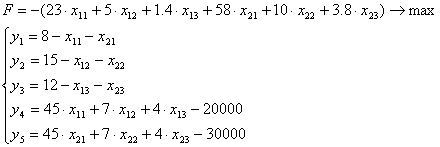
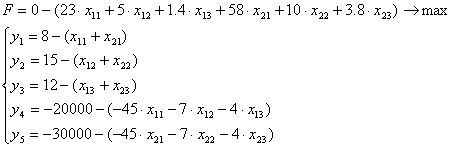
0 комментариев